【y=k】二次関数と直線の共有点、判別式について

1. 二次関数とy=kの共有点
二次関数と定数関数 \( y = k \) の共有点を求める方法は、二つの関数を連立させるだけです。
1.1. 二次関数と定数関数の方程式
二次関数は次の形で表されます。
\[ y = ax^2 + bx + c \]
ここで、\( a \)、\( b \)、\( c \) は定数です。
定数関数 \( y = k \) は、水平な直線で、常に \( y = k \) という一定の値を取ります。二次関数 \( y = ax^2 + bx + c \) と \( y = k \) を連立させるために、両方の \( y \) を等しくします。
\[ ax^2 + bx + c = k \]
これを整理して二次方程式の形にします。
\[ ax^2 + bx + (c – k) = 0 \]
この方程式を解くことで、二次関数と \( y = k \) の交点の \( x \) 座標を求めることができます。
1.2. 判別式を使った解の個数
\[ D = b^2 – 4a(c – k) \]
- \( D > 0 \) の場合、二次関数と \( y = k \) は2つの交点を持ちます。
- \( D = 0 \) の場合、1つの交点(接点)を持ちます。これは、二次関数が水平線 \( y = k \) に接する場合です。
- \( D < 0 \) の場合、二次関数と \( y = k \) は交点が存在しません。これは、二次関数が水平線と交わらない場合です。
1.3. グラフで考える方法
グラフを使った考え方について、判別式を使用せずに紹介します。まず、二次関数のグラフを考える際、二次関数 \( y = ax^2 + bx + c \) の軸や頂点がどのように動くかを見ていきましょう。特に、直線 \( y = k \) と二次関数の共有点が何個あるかを考えることがポイントです。$a>0$であると考えます。二次関数のグラフと直線 \( y = k \) の共有点の個数は、値 \( k \) によって変化します。
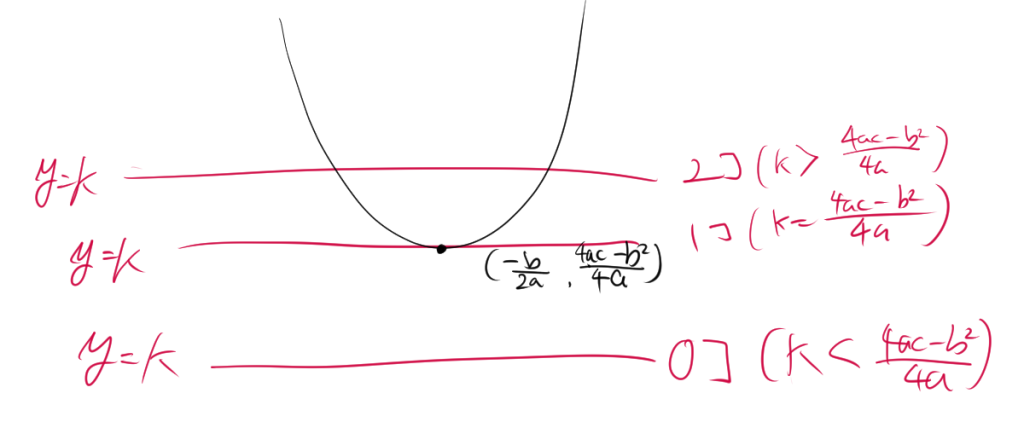
\( k < \dfrac{4ac – b^2}{4a} \) のとき
この場合、直線 \( y = k \) は、二次関数のグラフよりも下に位置しています。二次関数の頂点よりも低い位置に直線があるため、共有点は存在しません。よって、このときは 共有点は0個 です。
\( k = \dfrac{4ac – b^2}{4a} \) のとき
この場合、直線 \( y = k \) は、二次関数の頂点と同じ高さに位置します。つまり、二次関数のグラフと直線がちょうど接している状態です。このため、共有点は ちょうど1個 になります。
\( k > \dfrac{4ac – b^2}{4a} \) のとき
この場合、直線 \( y = k \) は、二次関数の頂点よりも高い位置にあります。したがって、二次関数のグラフは直線と2つの場所で交わることになります。このときは、 共有点が2個 になります。
直線 \( y = k \) が二次関数と交わる個数は、次のように整理できます。
- \( k < \frac{4ac – b^2}{4a} \) のとき → 共有点は 0個
- \( k = \frac{4ac – b^2}{4a} \) のとき → 共有点は 1個
- \( k > \frac{4ac – b^2}{4a} \) のとき → 共有点は 2個
2. 二次関数と直線の共有点
まず、二次関数と直線の方程式を考えます。二次関数は、次の形で表されます
\[ y = ax^2 + bx + c \]
ここで、\(a\)、\(b\)、\(c\) は定数です。直線は、次の形で表されます。
\[ y = mx + n \]
ここで、\(m\) は傾き、\(n\) は切片です。
この二つの方程式が共有点を持つとは、同じ \(x\) と \(y\) の値で両方の方程式が成り立つ点が存在することを意味します。二次関数 \(y = ax^2 + bx + c\) と直線 \(y = mx + n\) の共有点を求めるためには、この二つの方程式を連立させます。
\[ ax^2 + bx + c = mx + n \]
両辺から \(mx + n\) を引いて整理します
\[ ax^2 + bx + c – (mx + n) = 0 \]
整理すると
\[ ax^2 + (b – m)x + (c – n) = 0 \]
2.1. 判別式による交点の個数
\[ D = (b – m)^2 – 4a(c – n) \]
- \(D > 0\) の場合、二次関数と直線は2つの交点を持ちます。
- \(D = 0\) の場合、1つの交点(接点)を持ちます。この場合、直線は二次関数に接することになります。
- \(D < 0\) の場合、交点は存在しません。この場合、直線は二次関数と交わらず、二つのグラフは離れています。
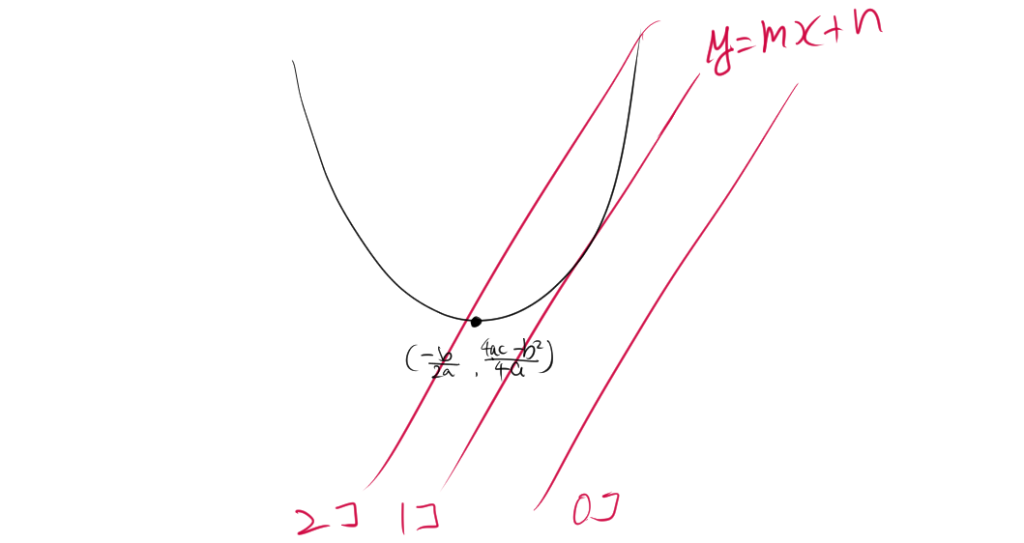
2.2. 判別式とグラフ
判別式と共有点の個数の関係をグラフにすると
3. 共有点の例題
3.1. 例題1
二つの方程式を連立させます。
\[ x^2 – 2x + 1 = 2x + 3 \]
これを整理します
\[ x^2 – 4x – 2 = 0 \]
次に判別式を計算します。
\[ D = (-4)^2 – 4(1)(-2) = 16 + 8 = 24 \]
判別式が正なので、共有点は2つあります。この方程式を解くと
\[ x = \frac{4 \pm \sqrt{24}}{2} = \frac{4 \pm 2\sqrt{6}}{2} = 2 \pm \sqrt{6} \]
したがって、交点の \(x\) 座標は \(2 + \sqrt{6}\) と \(2 – \sqrt{6}\) です。これらの値を直線の方程式に代入すると、対応する \(y\) 座標も求められます。求める座標は
$$(x,y)=( 2 + \sqrt{6},7+2\sqrt{6}),( 2 – \sqrt{6},7-2\sqrt{6})$$
3.2. 例題2
方程式を連立すると
\[ \begin{align*} 2x^2 – 4x + 1 &= 3 \\ 2x^2 – 4x – 2 &= 0 \\ x^2 – 2x – 1 &= 0 \end{align*} \]
次に判別式を計算します
\[ D = (-2)^2 – 4(1)(-1) = 4 + 4 = 8 \]
判別式が正なので、共有点は2つあります。この方程式を解くと
\[ x = \frac{2 \pm \sqrt{8}}{2} = 1 \pm \sqrt{2} \]
したがって、交点の \(x\) 座標は \( 1 + \sqrt{2} \) と \( 1 – \sqrt{2} \) です。対応する \(y\) 座標は、いずれも \( y = 3 \) です。したがって、求める座標は、
$$(x,y)=( 1 + \sqrt{2},3),( 1 – \sqrt{2},3)$$