数の分類（自然数、整数、有理数、無理数、実数、複素数）と記号の意味について

はるか

数の分類か。まあ、自然数は知ってるだろう。1から始まる正の整数。

ふゅか

うん、自然数は何かものを数えるときに使うよね！1, 2, 3,… みたいに♪ ちなみに集合記号では $\mathbb{N}$って書くんだね～

1. 数の分類

1.1. 自然数（Natural Numbers）

正の整数を表し、ものを数えるために使われる数です。

例: 1, 2, 3, 4, 5,…

自然数全体の集合は$\mathbb{N}$としてあらわされ、自然数の要素を$x\in\mathbb{N}$とあらわされる。記号「\(\mathbb{N}\)」は、Naturzahlen（ドイツ語で「自然数」）または「Natural Numger」の頭文字 N を使用します。

1.2. 整数（Integers）

自然数、0、および負の整数を含む数の集合です。

例: -3, -2, -1, 0, 1, 2, 3,…

整数全体の集合は$\mathbb{Z}$としてあらわされ、自然数の要素を$x\in\mathbb{Z}$とあらわされる。記号「\(\mathbb{Z}\)」は、Zahlen（ドイツ語で「数」または「整数」）の頭文字 Z から由来しています。

1.3. 有理数（Rational Numbers）

整数の比 \( \frac{p}{q} \) （\( q \neq 0 \)）として表せる数です。有限小数や循環小数も有理数です。

例: \( \frac{1}{2} \), \( -\frac{3}{4} \), 0.75, -2.333…

有理数全体の集合は$\mathbb{Q}$としてあらわされ、自然数の要素を$x\in\mathbb{Q}$とあらわされる。記号「\(\mathbb{Q}\)」は、Quotient（英語やドイツ語で「商」）の頭文字 Q から来ています。

1.4. 無理数（Irrational Numbers）

分数で表せない数で、無限小数かつ非循環です。例えば、\( \pi \) や \( \sqrt{2} \) などが無理数に該当します。

例: \( \pi \), \( \sqrt{2} \), \( e \)

\( \mathbb{R} \setminus \mathbb{Q} \) は、無理数全体の集合を表します。これは、実数全体 \( \mathbb{R} \) から有理数 \( \mathbb{Q} \) を除いたものです。無理数の要素を$x\in\mathbb{\mathbb{R} \setminus \mathbb{Q}}$とあらわされる。

1.5. 実数（Real Numbers）

有理数と無理数を含む数の集合で、数直線上の全ての点に対応する数です。自然数、整数、有理数、無理数がすべて含まれます。

例: -3, 0, 2.5, \( \pi \), \( \sqrt{2} \)

実数全体の集合は$\mathbb{R}$としてあらわされ、実数の要素を$x\in\mathbb{R}$とあらわされる。記号「\(\mathbb{R}\)」は、Real（英語で「実際の」や「現実の」）から頭文字 R を利用します

1.6. 複素数（Complex Numbers）

はるか

最後は複素数。

ふゅか

うん、複素数は実数と虚数が組み合わさった数だよね！例えば \( 2 + 3i \) とか。集合記号は \( \mathbb{C} \) で表すよ♪

複素数は、実数と虚数を組み合わせた数で、形は \( z = a + bi \) となります。ここで、\( a \) は実数部分、\( b \) は虚数部分、そして \( i \) は \( i^2 = -1 \) を満たす虚数単位です。実数は複素数の一部としても考えることができます（虚数部分が 0 の場合）。複素数の集合は、実数の範囲を超えて、より一般的な数の扱いを可能にします。

例: \( 2 + 3i \), \( -1 + 4i \), \( 3i \), 5（これは虚数部分が 0 であるため実数の一種）

複素数全体の集合は$\mathbb{C}$としてあらわされ、複素数の要素を$x\in\mathbb{C}$とあらわされる。Complex（英語で「複素数」）から頭文字 Cを利用します。

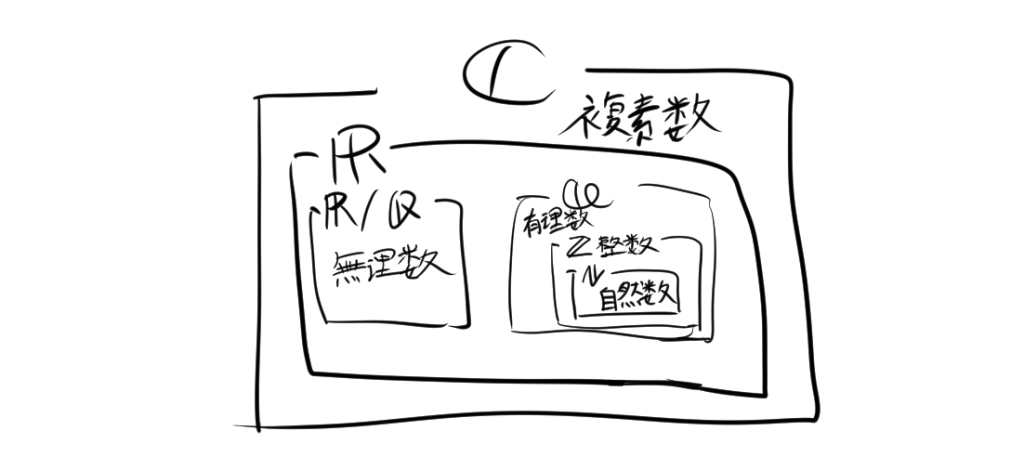
1.7. 包含関係

包含関係を図にすると次のようになります。

2. 数の分類の例題

次の数が、以下のどの種類に属するかを判定しなさい。

• 自然数
• 整数
• 有理数
• 無理数
• 実数
• 複素数

2.1. 問題 1:自然数

• 分類
  • 自然数 ✅
  • 整数 ✅
  • 有理数 ✅
  • 無理数 ❌
  • 実数 ✅
  • 複素数 ✅
• 考え方
  • 7 は正の整数であり、自然数です。
  • 自然数は整数、有理数、実数、複素数にも含まれます。
  • 無理数ではありません。

2.2. 問題 2:整数

• 分類
  • 自然数 ❌
  • 整数 ✅
  • 有理数 ✅
  • 無理数 ❌
  • 実数 ✅
  • 複素数 ✅
• 考え方
  • 3 は負の整数で、自然数ではありませんが、整数に含まれます。
  • 整数は有理数、実数、複素数にも含まれます。
  • 無理数ではありません。

2.3. 問題 3:有理数

• 分類
  • 自然数 ❌
  • 整数 ❌
  • 有理数 ✅
  • 無理数 ❌
  • 実数 ✅
  • 複素数 ✅
• 考え方
  • \( \frac{4}{5} \) は分数であり、有理数です。
  • 自然数や整数には該当しませんが、実数および複素数に含まれます。
  • 無理数ではありません。

2.4. 問題 4:無理数

• 分類
  • 自然数 ❌
  • 整数 ❌
  • 有理数 ❌
  • 無理数 ✅
  • 実数 ✅
  • 複素数 ✅
• 考え方
  • \( \sqrt{2} \) は無理数であり、整数や有理数ではありません。
  • 実数および複素数に含まれます。

2.5. 問題 5:複素数

• 分類
  • 自然数 ❌
  • 整数 ❌
  • 有理数 ❌
  • 無理数 ❌
  • 実数 ❌
  • 複素数 ✅
• 考え方
  • \( 2 + 3i \) は複素数であり、自然数や整数、有理数、実数には含まれません。
  • 無理数でもありません。

2.6. 問題 6:無理数

• 分類
  • 自然数 ❌
  • 整数 ❌
  • 有理数 ❌
  • 無理数 ✅
  • 実数 ✅
  • 複素数 ✅
• 考え方
  • \( \pi \) は無理数であり、実数および複素数に含まれます。
  • 自然数や整数、有理数には該当しません。