数値微分の基本！前進差分法、後退差分法、および中心差分法について

はるか

今日は数値微分の基本について話すよ。具体的には、前進差分法、後退差分法、そして中心差分法。

ふゅか

解析的に微分できないときに有効な方法だよね！機械学習の損失関数とか！

数値微分の基本的な方法

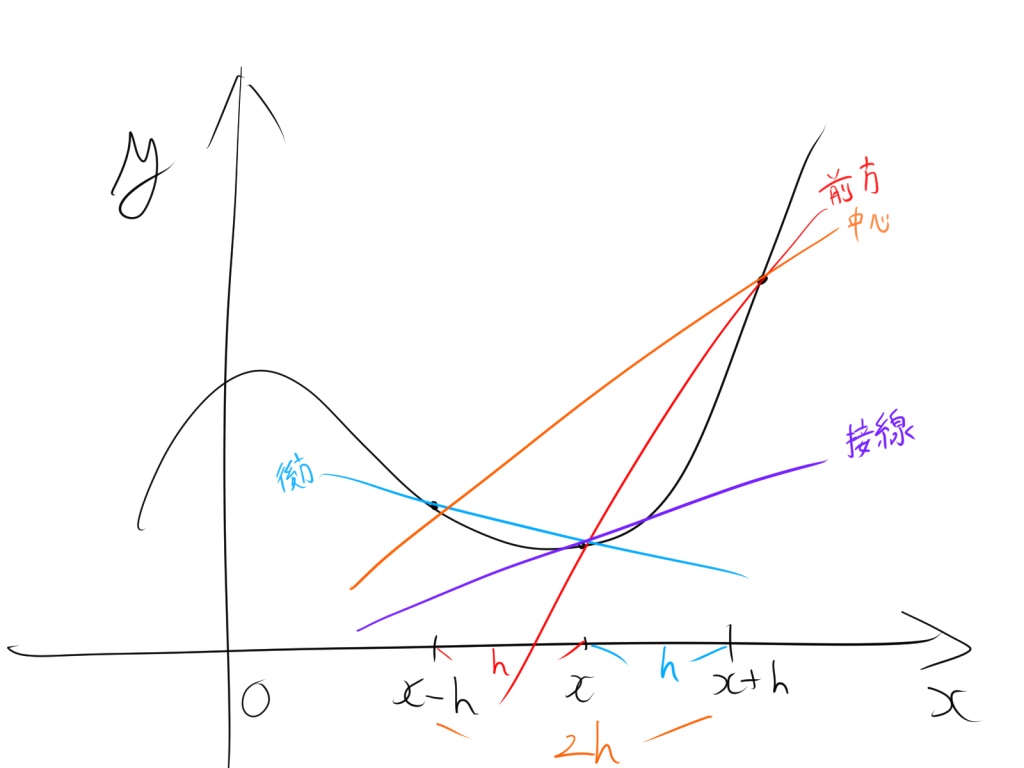
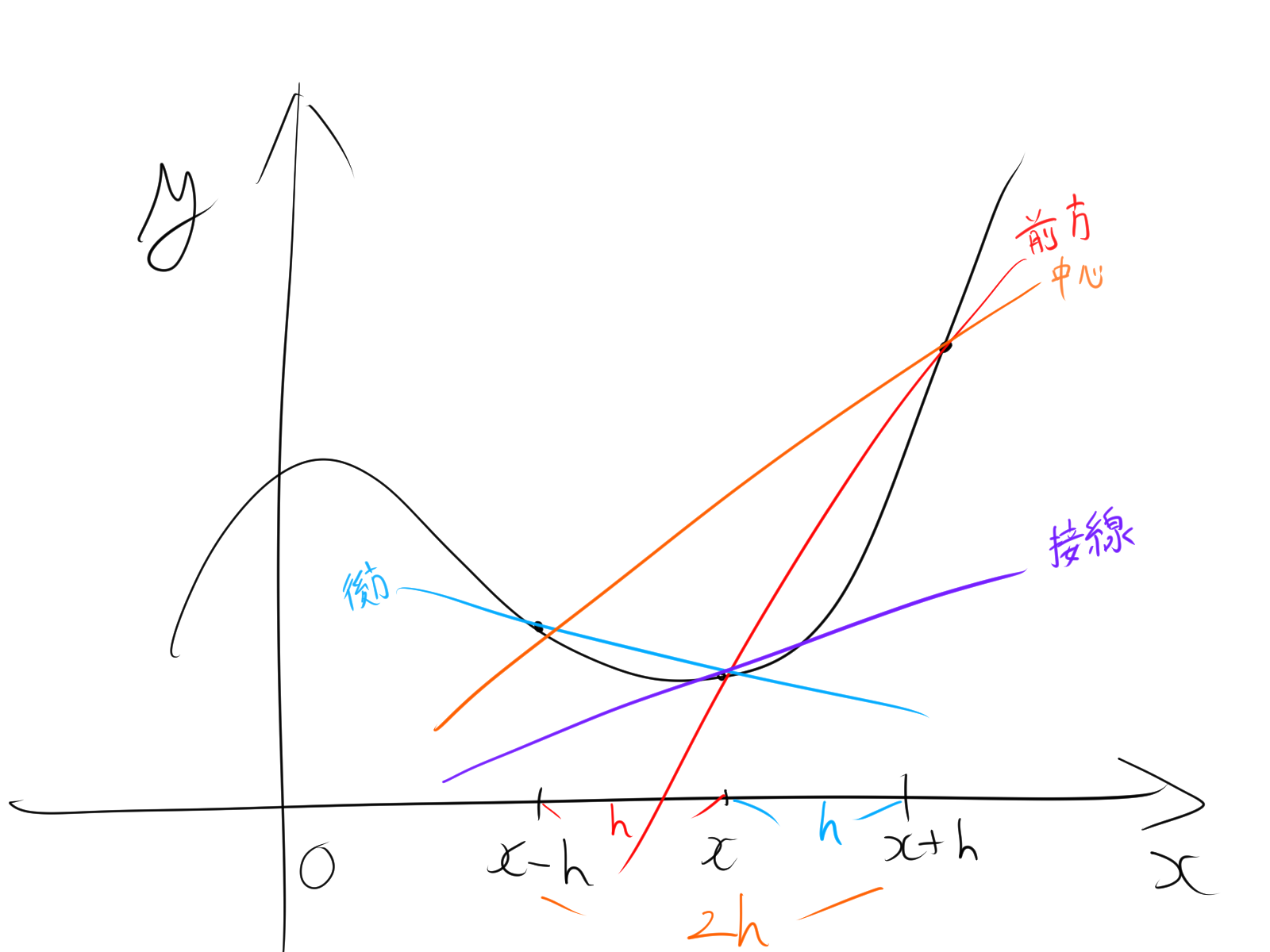
数値微分は、関数の導関数（微分）を数値的に求める手法です。これは、関数が解析的に微分できない場合や、関数の式が知られていない場合に特に有用です。数値微分の基本的な考え方は、関数 \( f(x) \) の微分を有限の差分を用いて近似することです。ここでは、最も一般的な方法である前進差分法、後退差分法、および中心差分法を紹介します。

前進差分法（Forward Difference Method）

後退差分法（Backward Difference Method）

中心差分法（Central Difference Method）

実践例

はるか

次に、Pythonでの実装例を見せるよ。

ふゅか

数値微分の方法を使って、具体的にどんな風に計算するか見てみるね♪

import numpy as np

def forward_difference(f, x, h=1e-5):
    return (f(x + h) - f(x)) / h

def backward_difference(f, x, h=1e-5):
    return (f(x) - f(x - h)) / h

def central_difference(f, x, h=1e-5):
    return (f(x + h) - f(x - h)) / (2 * h)

# 関数の定義
def func(x):
    return np.sin(x)

# 微分の計算
x = np.pi / 4

forward_diff = forward_difference(func, x)
backward_diff = backward_difference(func, x)
central_diff = central_difference(func, x)

print(f"Forward difference of sin(x) at x = {x} is approximately {forward_diff}")
print(f"Backward difference of sin(x) at x = {x} is approximately {backward_diff}")
print(f"Central difference of sin(x) at x = {x} is approximately {central_diff}")

これにより、指定された点 \( x = \pi/4 \) における \( \sin(x) \) の数値微分を3つの異なる方法で計算できます。

以下はそれぞれの関数の説明です。

1. 前進差分法の関数

   def forward_difference(f, x, h=1e-5):
       return (f(x + h) - f(x)) / h

2. 後退差分法の関数

   def backward_difference(f, x, h=1e-5):
       return (f(x) - f(x - h)) / h

3. 中心差分法の関数

   def central_difference(f, x, h=1e-5):
       return (f(x + h) - f(x - h)) / (2 * h)

結果

これらの関数を使って計算した結果は以下のようになります。

print(f"Forward difference of sin(x) at x = {x} is approximately {forward_diff}")
print(f"Backward difference of sin(x) at x = {x} is approximately {backward_diff}")
print(f"Central difference of sin(x) at x = {x} is approximately {central_diff}")

はるか

これで、指定された点 \( x = \pi/4 \) における \( \sin(x) \) の数値微分を3つの異なる方法で計算できるよ。

ふゅか

うん、結果を見てみると、それぞれの方法で微分の値がどう違うかがわかるね！前進差分法、後退差分法、中心差分法の結果を比べてみてね☆