Octaveの行列演算・逆行列・固有値・演習問題について

Octaveの行列演算は、行列の足し算、引き算、掛け算、転置、逆行列など、様々な操作をサポートしています。

1. 行列の基本的な操作

1.1. 行列の定義

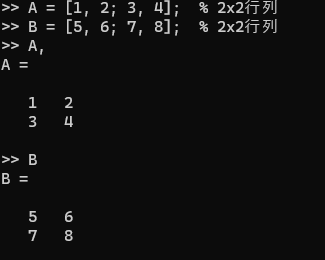
行列は、[]内に要素をカンマやスペースで区切って定義します。行列の各行はセミコロンで区切ります。

A = [1, 2; 3, 4];  % 2x2行列
B = [5, 6; 7, 8];  % 2x2行列

1.2. 行列の足し算・引き算

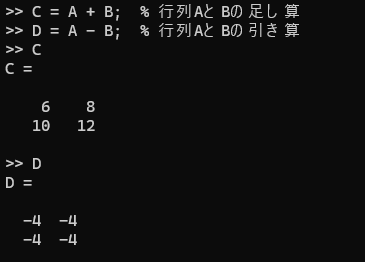
同じサイズの行列同士で、対応する要素を足し引きします。

C = A + B;  % 行列AとBの足し算
D = A - B;  % 行列AとBの引き算

1.3. 行列の掛け算

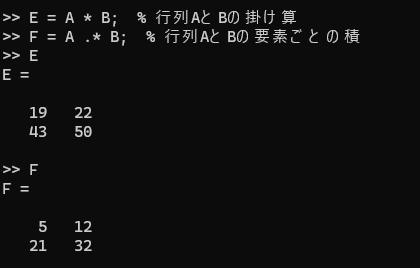
行列の掛け算は、通常の行列の積演算を行います。

E = A * B;  % 行列AとBの掛け算

要素ごとの積（アダマール積）を求める場合は、.*を使用します。

F = A .* B;  % 行列AとBの要素ごとの積

1.4. 転置行列

行列の転置は、'を使って行います。

G = A';  % 行列Aの転置

1.5. 逆行列

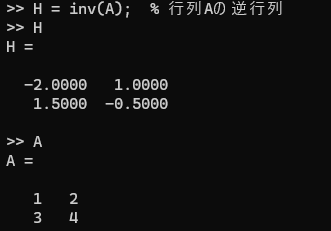
行列の逆行列は、inv関数を使用します。ただし、逆行列が存在するためには行列が正則である必要があります。

H = inv(A);  % 行列Aの逆行列

1.6. 行列の行列式

行列の行列式は、det関数を使用して計算できます。

det_A = det(A);  % 行列Aの行列式

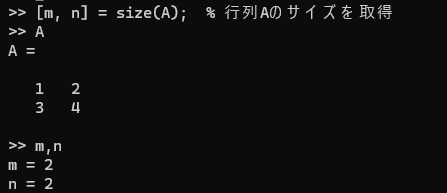
1.7.  行列のサイズの確認

行列のサイズは、size関数で確認できます。

[m, n] = size(A);  % 行列Aのサイズを取得

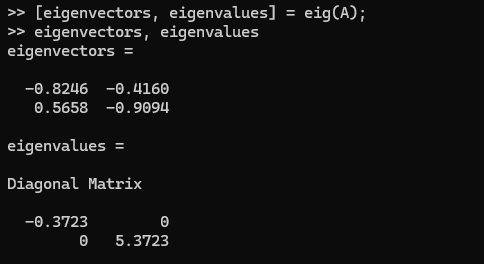
1.8. 行列の固有値と固有ベクトル

行列の固有値と固有ベクトルは、eig関数を使用して計算します。

[eigenvectors, eigenvalues] = eig(A);  % 行列Aの固有値と固有ベクトル

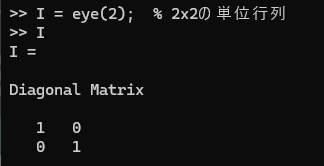
1.9. 単位行列

単位行列は、eye関数を使用して生成します。

I = eye(2);  % 2x2の単位行列

1.10. ゼロ行列

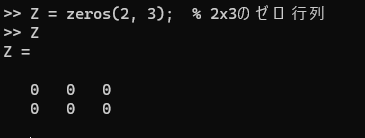
全ての要素が0の行列は、zeros関数を使用して生成します。zeros(m,n)で要素がすべて零のm×n行列を作成することができます。

Z = zeros(2, 3);  % 2x3のゼロ行列

1.11. 同じ任意の値の行列

任意の値で埋められた行列は、ones関数を使用して生成します。ones関数ですべての要素を1にして、任意の値をかけることで、行列を作成することができます。

O = ones(3, 2) * 7;  % 3x2の全ての要素が7の行列

2. 演習問題

2.1. 問題1: 対称行列の判定

まず、行列 \( A \) を定義します。この行列は3×3の行列で、各要素は次のように与えられています。

\[ A = \begin{pmatrix} 1 & 7 & 3 \\ 7 & 4 & -5 \\ 3 & -5 & 6 \end{pmatrix} \]

Octaveでは、行列を次のように定義します。

A = [1, 7, 3; 7, 4, -5; 3, -5, 6];

ここで、[]内に行列の要素をカンマやスペースで区切って入力し、行をセミコロン ; で区切ります。

次に、行列 \( A \) の転置行列 \( A^T \) を計算します。転置行列とは、元の行列の行と列を入れ替えた行列のことです。Octaveでは、転置行列を次のように計算します。

AT = A';

ここで、'（アポストロフィー）を使って、行列 \( A \) を転置しています。

行列が対称行列であるためには、元の行列とその転置行列が等しい必要があります。これを確認するために、Octaveのisequal関数を使用します。この関数は、2つの行列が完全に同一かどうかを比較し、等しければ true（Octaveでは 1）、等しくなければ false（Octaveでは 0）を返します。

is_symmetric = isequal(A, AT);

ここで、is_symmetric が 1 であれば行列 \( A \) は対称行列、0 であれば対称行列ではありません。

コードを実行すると、次のような出力が得られます。

行列Aが対称行列か: 1

この出力が示すように、is_symmetric が 1 なので、行列 \( A \) は対称行列であることが確認できます。

ここまでの手順をまとめると、以下のようなコードになります。

% 行列Aの定義
A = [1, 7, 3; 7, 4, -5; 3, -5, 6];
% 転置行列A^Tの計算
AT = A';

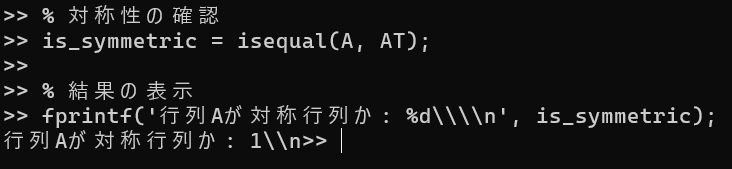
% 対称性の確認
is_symmetric = isequal(A, AT);

% 結果の表示
fprintf('行列Aが対称行列か: %d\\\\n', is_symmetric);

2.2. 問題2:対称行列の固有値と固有ベクトル

まず、行列 \( B \) を定義します。この行列は3×3の行列で、各要素は次のように与えられています。

\[ B = \begin{pmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{pmatrix} \]

Octaveでこの行列を定義するには、次のように入力します。

B = [2, -1, 0; -1, 2, -1; 0, -1, 2];

行列 \( B \) が対称行列であるかを確認するには、転置行列 \( B^T \) を計算し、元の行列 \( B \) と比較します。

転置行列 \( B^T \) を計算し、元の行列 \( B \) と比較するコードは次のようになります。

BT = B';                % 転置行列B^Tの計算
is_symmetric_B = isequal(B, BT);  % BとB^Tが等しいか確認

is_symmetric_B が 1 であれば、行列 \( B \) は対称行列です。

対称行列の固有値は全て実数であり、固有ベクトルは直交するという性質があります。これを確認するために、まず固有値と固有ベクトルを計算します。

[V_B, D_B] = eig(B);  % 固有ベクトルV_Bと固有値D_Bの計算

ここで、D_B には固有値が対角行列として格納され、V_B には対応する固有ベクトルが列ベクトルとして格納されます。

次に、固有値が全て実数であることを確認します。固有値が実数かどうかを調べるには、次のコードを使用します。

eigenvalues_B = diag(D_B);       % 固有値を取り出す
are_real_B = all(isreal(eigenvalues_B));  % 全ての固有値が実数か確認

are_real_B が 1 であれば、固有値は全て実数です。

固有ベクトルが直交しているかどうかを確認するには、固有ベクトル行列 \( V_B \) を用いて次の計算を行います。

orthogonality_check_B = V_B' * V_B;  % V_B' * V_B が単位行列に近いか確認

orthogonality_check_B が単位行列 \( I \) に近い値であれば、固有ベクトルは直交しています。（場合によっては固有ベクトルが近似値になるため）

最後に、対称性、固有値が実数であるか、固有ベクトルが直交しているかどうかを表示します。

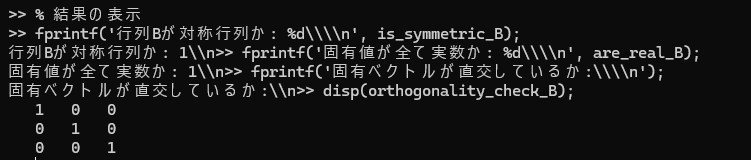
fprintf('行列Bが対称行列か: %d\\\\n', is_symmetric_B);
fprintf('固有値が全て実数か: %d\\\\n', are_real_B);
fprintf('固有ベクトルが直交しているか:\\\\n');
disp(orthogonality_check_B);

全ての手順をまとめたコードは以下の通りです。

% 行列Bの定義
 B = [2, 0, 0; 0, 2,0; 0, 0, 2];
% 転置行列B^Tの計算
BT = B';

% 対称性の確認
is_symmetric_B = isequal(B, BT);

% 固有値と固有ベクトルの計算
[V_B, D_B] = eig(B);

% 固有値が全て実数かの確認
eigenvalues_B = diag(D_B);
are_real_B = all(isreal(eigenvalues_B));

% 固有ベクトルが直交しているかの確認
orthogonality_check_B = V_B' * V_B;

% 結果の表示
fprintf('行列Bが対称行列か: %d\\\\n', is_symmetric_B);
fprintf('固有値が全て実数か: %d\\\\n', are_real_B);
fprintf('固有ベクトルが直交しているか:\\\\n');
disp(orthogonality_check_B);