Octaveのベクトル演算・内積・外積・ノルムについて

1. 基本的な操作

1.1. ベクトルの作成

ベクトルは1次元の配列として表現されます。行ベクトルと列ベクトルがあり、それぞれの作成方法は以下の通りです。

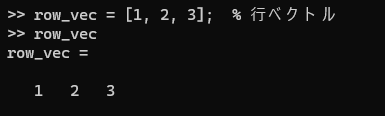
行ベクトル

row_vec = [1, 2, 3];  % 行ベクトル

列ベクトル

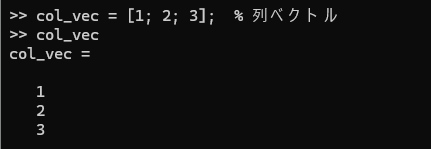
col_vec = [1; 2; 3];  % 列ベクトル

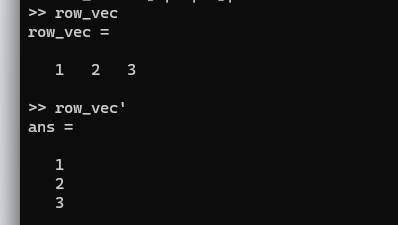
1.2. ベクトルの転置

ベクトルに対して'をつけるとベクトルを転置することができる。

1.3. 要素ごとの演算

Octaveでは、ベクトル同士の要素ごとの演算を簡単に行うことができます。たとえば、要素ごとの加算、減算、乗算、除算は以下のように行います。

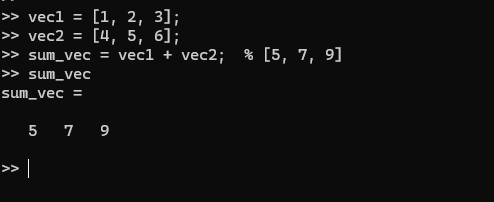
要素ごとの加算

vec1 = [1, 2, 3];
vec2 = [4, 5, 6];
sum_vec = vec1 + vec2;  % [5, 7, 9]

要素ごとの乗算

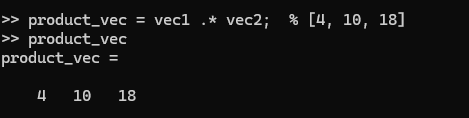
product_vec = vec1 .* vec2;  % [4, 10, 18]

.* は要素ごとの乗算を示します。* だけを使うと行列積を計算するので注意が必要です。

要素ごとの除算

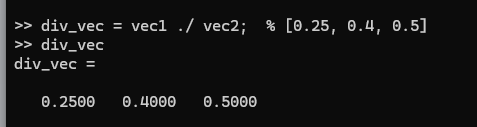
div_vec = vec1 ./ vec2;  % [0.25, 0.4, 0.5]

./ も要素ごとの演算を示します。

2. ベクトルの演算

2.1. 内積

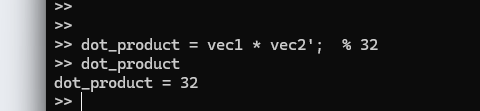
内積は、2つのベクトルの要素ごとの積を合計したものです。行列積として計算できます。

dot_product = vec1 * vec2';  % 32

ここで、vec2' はベクトル vec2 の転置です。

2.2. 外積

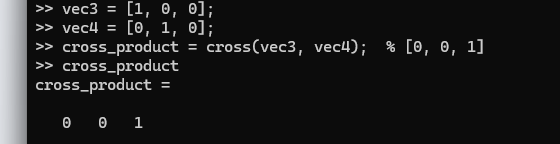
3次元ベクトル同士の外積は、以下のように計算されます。

vec3 = [1, 0, 0];
vec4 = [0, 1, 0];
cross_product = cross(vec3, vec4);  % [0, 0, 1]

2.3. ベクトルのノルム

ベクトルのノルム（長さ）を求めるには norm 関数を使用します。

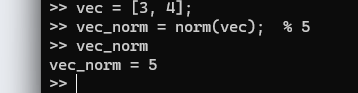
vec = [3, 4];
vec_norm = norm(vec);  % 5

この場合は、$\mathbb{R}^2$のユークリッドノルムを計算します。

3. 便利な操作

3.1. ベクトルの要素へのアクセス

ベクトルの特定の要素にアクセスするにはインデックスを使用します。Octaveではインデックスは1から始まります。

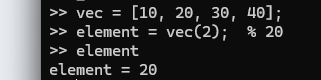
vec = [10, 20, 30, 40];
element = vec(2);  % 20

また、範囲を指定して複数の要素を取り出すこと（スライス）もできます。

3.2. ベクトルのスライス操作

ベクトルの一部をスライス（切り出し）することが可能です。

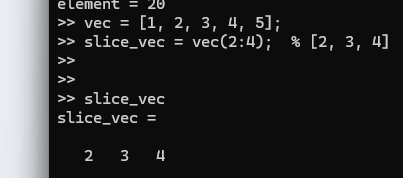
vec = [1, 2, 3, 4, 5];
slice_vec = vec(2:4);  % [2, 3, 4]

3.3. ベクトルの連結

複数のベクトルを連結して1つのベクトルにすることができます。

行ベクトルの連結

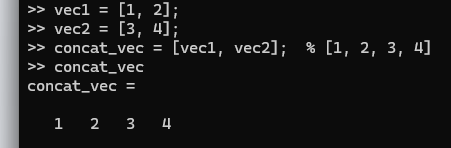
vec1 = [1, 2];
vec2 = [3, 4];
concat_vec = [vec1, vec2];  % [1, 2, 3, 4]

列ベクトルの連結

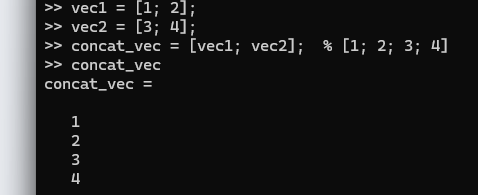
vec1 = [1; 2];
vec2 = [3; 4];
concat_vec = [vec1; vec2];  % [1; 2; 3; 4]

3.4. ベクトルの初期化

特定の値でベクトルを初期化することができます。

すべての成分がゼロのベクトルを生成する。zeros(m,n)で要素がすべて零のm×n行列を生成できるため、zeros(1,n)で成分がゼロの1×nのベクトルを生成できる。

zero_vec = zeros(1, 5);  % [0, 0, 0, 0, 0]

すべての成分が1のベクトル。zeros(m,n)で要素がすべて1のm×n行列を生成できるため、zeros(1,n)で成分が1の1×nのベクトルを生成できる。

ones_vec = ones(1, 3);  % [1, 1, 1]

ランダムなベクトルを生成する。rand(m,n)で要素がランダムなm×n行列を生成できるため、rand(1,n)で1×nのベクトルを生成できる。

rand_vec = rand(1, 4);