1の3乗根の複素数ωの意味と性質、具体例について

はるか

$ω$は1の3乗根の解の一つ。

ふゅか

そうだね！この$ω$を使うと、たくさんの面白い性質が見つかるのよね♪

1. 複素数 ω

1.1. $x^{3}-1=0$ の方程式の解について

まず、$x^{3}-1=0$ を因数分解してみます。

\[ (x – 1)(x^{2} + x + 1) = 0 \]

この式から、$x – 1 = 0$ で $x = 1$ となる解が得られます。一方、$x^{2} + x + 1 = 0$ についても解を求めてみましょう。この二次方程式を解の公式で計算すると、次のようになります。

\[ x = \frac{-1 \pm \sqrt{3}i}{2} \]

したがって、この方程式の解は $x = 1$ と $x = \frac{-1+\sqrt{3}i}{2}$、および $x = \frac{-1-\sqrt{3}i}{2}$ の 3 つです。このうち、$ω$ として $\frac{-1+\sqrt{3}i}{2}$ を取ります。

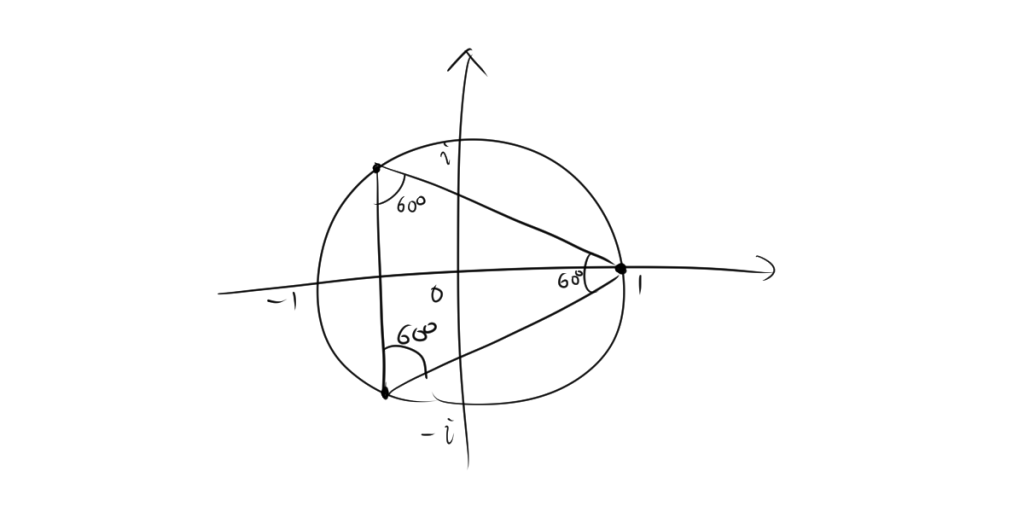
複素数平面上にこの解を書くと円上に存在して、次のようになります。

2. 複素数ωの性質

ここで、$ω = \frac{-1+\sqrt{3}i}{2}$ とすると、以下のような興味深い性質が得られます。

2.1. ωの2乗

$ω^2$ を計算すると、次のようになります。

\[ ω^2 = \left( \frac{-1+\sqrt{3}i}{2} \right)^2 = \frac{1 – 3 + 2\sqrt{3}i}{4} = \frac{-1 – \sqrt{3}i}{2} =\overline \omega\]

この結果から、$ω^{2}$ がもう一つの解 $\frac{-1-\sqrt{3}i}{2}$ と一致することが分かります。この $ω$ と $ω^2$ は、まるで双子のような性質を持っています。

また、方程式$x^{2} + x + 1 = 0$ に $ω$ を代入すると、

\[ ω^{2} + ω + 1 = 0 \]

これにより、$ω^{2} = -ω – 1$ であることが確認できます。したがって、

$$ω^{2} = -ω – 1 = \overline{ω}$$

はるか

$ω^{2}$は$ \overline{ω}$、つまり複素共役になる。

ふゅか

そうなの！$ω^2$を計算すると、ちゃんと$ \overline{ω}$と一致するんだ。まるで双子みたいで面白いね！

2.2. ωの3乗

$x^{3} – 1 = 0$ に $ω$ を代入すると、\[ ω^{3} – 1 = 0 \quad \Leftrightarrow \quad ω^{3} = 1 \]

これにより、$ω$ の 3 乗が 1 になることが分かります。

ふゅか

あとね、$ω^3$は$1$になるの。$x^{3}-1=0$に$ω$を代入して確認するとわかるよ☆

はるか

1の3乗根の解の一つだから当然。

3. 例題

3.1. 例題 1: \( \omega^{1000} + \omega \)

\( \omega^3 = 1 \)より、\( \omega^{1000} \) は

\[ \omega^{1000} = (\omega^3)^{333}\omega \]

次に、求めたい式は次の通りです。

\[ \omega^{1000} + \omega = \omega + \omega = 2\omega \]

\(\omega = \frac{-1+\sqrt{3}i}{2}\) なので、

\[ \omega^{1000} + \omega = 2\omega = -1 + \sqrt{3}i \]

3.2. 例題 2: \( \omega^5 – \overline{\omega}^4 \)

\(\omega^3 = 1\) であるため、\(\omega^5\) は

\[ \omega^5 = \omega^3 \cdot \omega^2 =\omega^2 \]

次に、\(\overline{\omega}^4\) の計算します。\(\overline{\omega}^3 = 1\) であるため、

$$\overline{\omega}^4 = \overline{\omega}$$となります。したがって、

\[ \omega^5 – \overline{\omega}^4 = \omega^2 – \overline{\omega} \]

$\overline{\omega}=\omega^2 $より、

\[ \omega^5 – \overline{\omega}^4 = 0 \]