【片側極限】右側極限と左側極限の意味と計算方法について

1. 極限とは
まず、関数の極限とは何かを簡単に説明します。ある関数 \( f(x) \) が、変数 \( x \) が特定の値 \( a \) に近づくときに、\( f(x) \) が$\alpha$に近づくことを極限と呼びます。以下のようになります。
2. 片側極限
片側極限は、\( x \) が特定の値 \( a \) に「一方の方向」から近づくときの関数の極限です。これはさらに以下の2つに分けられます。
2.1. 左側極限
\[ \lim_{x \to a-0} f(x) \]
2.2. 右側極限
\[ \lim_{x \to a+0} f(x) \]
2.3. 片側極限と極限
\[ \lim_{x \to a} f(x)=\alpha \]
3. 片側極限の具体例
3.1. 例1
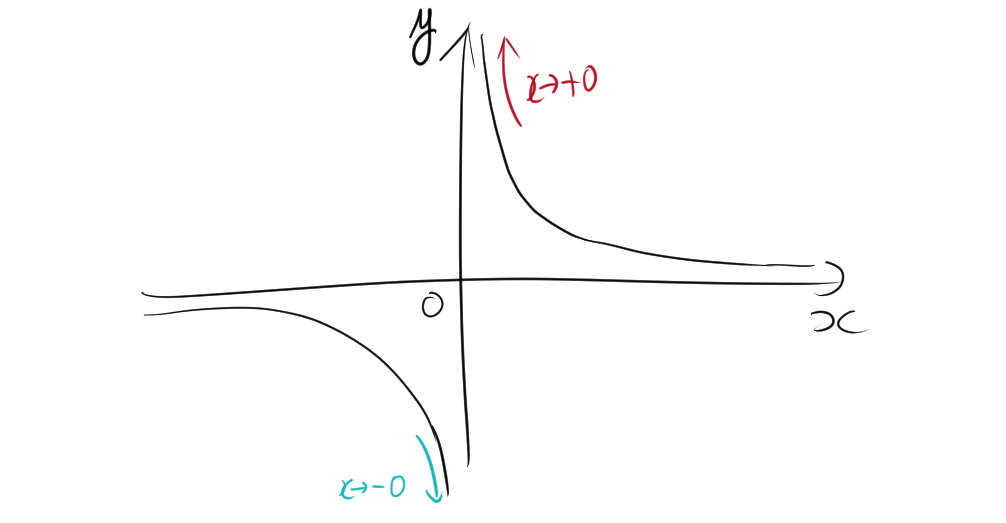
関数$f(x)=\frac{1}{x}$の片側極限を求めます。
左側極限を求める。
\[ \lim_{x \to 0^-} \frac{1}{x} = -\infty \]
右側極限を求める。
\[ \lim_{x \to 0^+} \frac{1}{x} = \infty \]
3.2. 例2
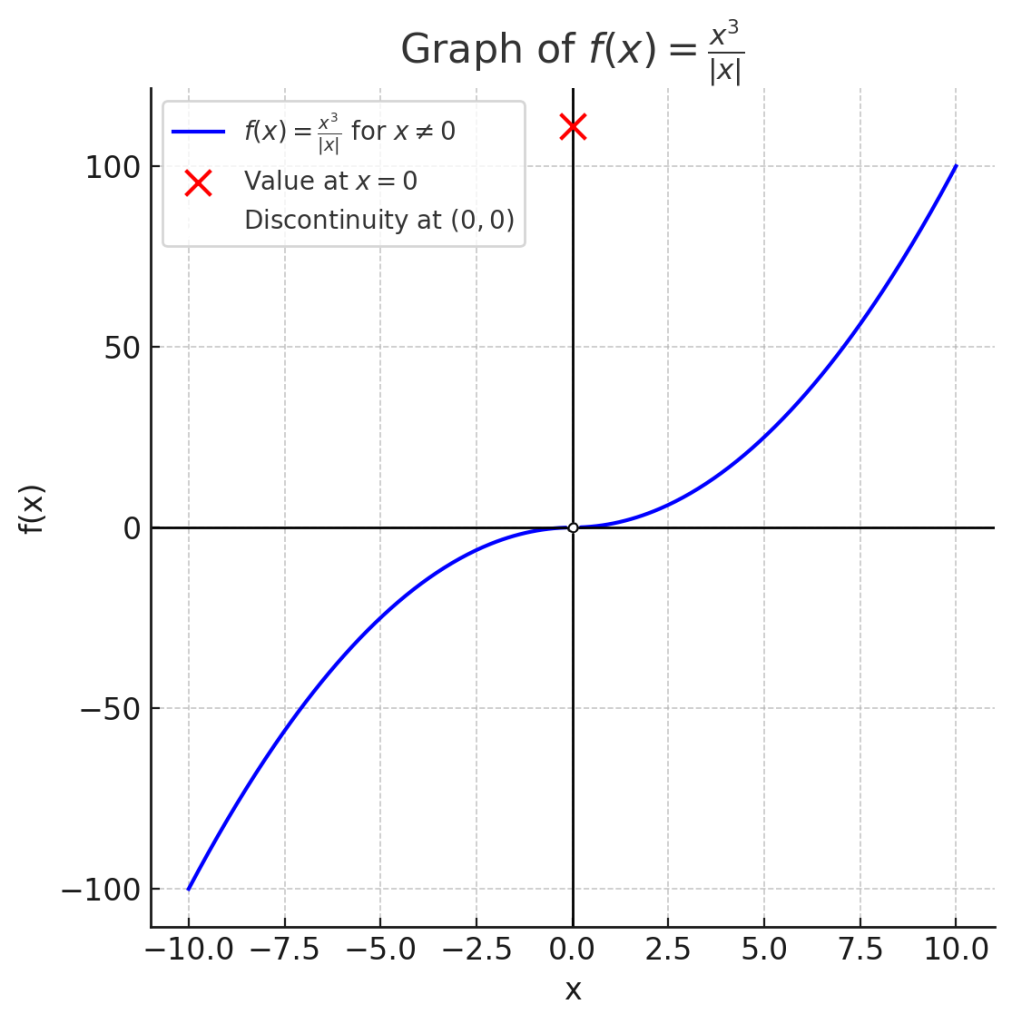
関数$f(x)$を次のように定義します。
$$f(x) =\begin{cases} &\frac{x^3}{|x|} & (x\neq 0) \\ &111 & (x = 0) \\ \end{cases}$$
の \( x \to 0 \) の場合の片側極限を求めます。
左側極限は0より小さい値から近づいてくので、絶対値は$|x|=-x$となるので、
\[ \lim_{x \to -0} \frac{x^3}{|x|} = \lim_{x \to -0} -x^2= 0 \]
右側極限は0より大きい値から近づいてくので、絶対値は$|x|=x$となるので、
\[ \lim_{x \to -0} \frac{x^3}{|x|} = \lim_{x \to -0} x^2= 0 \]
以上の結果より、
$$\lim_{x \to 0} f(x) =0 $$
となる。
4. 例題
4.1. 例題 1
\[ f(x) = \begin{cases} 3x – 1 & (x < 2) \\ x^2 + 1 & (x \geq 2) \end{cases} \]
右側極限 \( \displaystyle\lim_{x \to 2+0} f(x) \)を求める。
\( f(x) = x^2 + 1 \) (x ≥ 2 なのでこの式を使用)
\( \lim_{x \to 2+0} f(x) = 2^2 + 1 = 5 \)
左側極限 \( \displaystyle\lim_{x \to 2-0} f(x) \)を求める。
\( f(x) = 3x – 1 \) (x < 2 なのでこの式を使用)
$$ \lim_{x \to 2-0} f(x) = 3 \cdot 2 – 1 = 5 $$
4.2. 例題 2
\[ g(x) = \begin{cases} x + 2 & (x \geq 0) \\ x^2 – 3 & (x < 0) \end{cases} \]
右側極限 \(\displaystyle\lim_{x \to +0} g(x) \)を求める。
\( g(x) = x + 2 \) (x ≥ 0 なのでこの式を使用)
$$ \lim_{x \to 0+0} g(x) = 0 + 2 = 2 $$
左側極限 \(\displaystyle\lim_{x \to -0} g(x) \)を求める。
\( g(x) = x^2 – 3 \) (x < 0 なのでこの式を使用)
$$ \lim_{x \to 0-0} g(x) = 0^2 – 3 = -3 $$
4.3. 例題 3
\[ h(x) = \begin{cases} \frac{1}{x – 1} & (x < 1) \\ \frac{2}{x – 1} & (x > 1) \end{cases} \]
右側極限\( \displaystyle\lim_{x \to 1+0} h(x) \)を求める。
\( h(x) = \frac{2}{x – 1} \) (x > 1 なのでこの式を使用)
$$ \lim_{x \to 1+0} h(x) = \frac{2}{1 – 1} = \infty $$
左側極限\( \displaystyle\lim_{x \to 1-0} h(x) \)を求める。
\( h(x) = \frac{1}{x – 1} \) (x < 1 なのでこの式を使用)
$$\lim_{x \to 1-0} h(x) = \frac{1}{1 – 1} = -\infty $$