正射影ベクトルの定義・具体例・垂直なベクトル・計算問題について

1. 正射影ベクトルとは
\[ \mathbf{p} = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|^2} \mathbf{b} \]
1.1. 正射影ベクトルの計算例
例えば、\( \mathbf{a} = (3, 4) \) と \( \mathbf{b} = (1, 2) \) の場合、
内積 \( \mathbf{a} \cdot \mathbf{b} = 3 \times 1 + 4 \times 2 = 11 \)
ベクトル \( \mathbf{b} \) の大きさの二乗 \( \mathbf{b} \cdot \mathbf{b} = 1^2 + 2^2 = 5 \)
正射影ベクトル \( \mathbf{p} = \frac{11}{5} \mathbf{b} = \left(\frac{11}{5}, \frac{22}{5}\right) \)
1.2. 正射影ベクトルと垂直なベクトル
$$\mathbf{a}-\mathbf{p}=\mathbf{a}- \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|^2} \mathbf{b} $$
このとき、\(\mathbf{a}\) と \(\mathbf{b}\) の正射影ベクトル \(\mathbf{p}\) と垂直なベクトル \(\mathbf{v}\) を次のように定義します。
\[ \mathbf{v} = \mathbf{a} – \mathbf{p} \]
このベクトル \(\mathbf{v}\) が \(\mathbf{b}\) に垂直であることを証明するためには、\(\mathbf{v}\) と \(\mathbf{b}\) の内積がゼロになることを示す。
\[ \mathbf{v} \cdot \mathbf{b} = (\mathbf{a} – \mathbf{p}) \cdot \mathbf{b} \]
$$=\mathbf{a} \cdot \mathbf{b} – \mathbf{p} \cdot \mathbf{b}$$
$$=\mathbf{a} \cdot \mathbf{b} – \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|^2} \mathbf{b} \cdot \mathbf{b}$$
$$=\mathbf{a} \cdot \mathbf{b} – \mathbf{a} \cdot \mathbf{b} =0$$
したがって、$\mathbf{a}-\mathbf{p}$と$\mathbf{b}$は0ベクトルではないことと内積が0であるため、$\mathbf{a}-\mathbf{p}$と$\mathbf{b}$は垂直である。
2. 正射影ベクトルの導出
2.1. 導出1(垂直なベクトルの内積を利用)
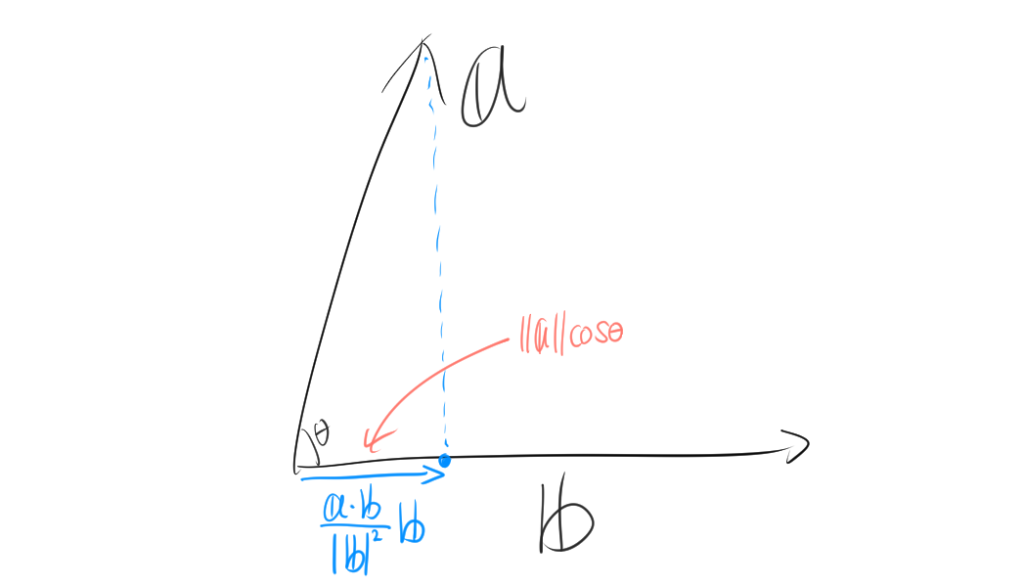
ベクトル \( \mathbf{a} \) をベクトル \( \mathbf{b} \) に正射影したベクトル \( \mathbf{p} \) を求めたい。ここで、画像からもわかるように、\( \mathbf{p} \) はベクトル \( \mathbf{b} \) に平行なベクトルです。従って、\( \mathbf{p} \) は次の形で表されます。($\theta >\frac{\pi}{2}$のときは、マイナスがつく。)
\[ \mathbf{p} = k \mathbf{b} \]
ベクトル \( \mathbf{p} \) は \( \mathbf{b} \) の方向に沿ったベクトルであり、\( \mathbf{a} \) と \( \mathbf{p} \) の間のベクトル差 \( \mathbf{a} – \mathbf{p} \) は、ベクトル \( \mathbf{b} \) に直交します。すなわち、
\[ \mathbf{b} \cdot (\mathbf{a} – \mathbf{p}) = 0 \]
この内積を展開すると、
\[ \mathbf{b} \cdot \mathbf{a} – \mathbf{b} \cdot \mathbf{p} = 0 \]
になります。さらに、\( \mathbf{p} = k \mathbf{b} \) であるため、
\[ \mathbf{b} \cdot \mathbf{a} – k (\mathbf{b} \cdot \mathbf{b}) = 0 \]
これを \( k \) について解くと、
\[ k = \frac{\mathbf{b} \cdot \mathbf{a}}{\|\mathbf{b}\|^2} \]
したがって、正射影ベクトル \( \mathbf{p} \) は次のように表されます。
\[ \mathbf{p} = k \mathbf{b} = \frac{\mathbf{b} \cdot \mathbf{a}}{\|\mathbf{b}\|^2} \mathbf{b} \]
2.2. 導出2 ($\cos\theta$と内積を利用)
$\mathbf{b}$の単位ベクトルを$\mathbf{e_b}$と置きます。
このとき、正射影ベクトル$\mathbf{p}$は次のようになります。($\theta >\frac{\pi}{2}$のときは、マイナスがつく。)
$$\mathbf{p} = (\|\mathbf{a}\|\cos\theta) \mathbf{e_b}$$
$$= (\|\mathbf{a}\|\cos\theta) \dfrac{\mathbf{b}}{\|\mathbf{b}\|}$$
$\cos\theta = \dfrac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}$より、
$$=\|\mathbf{a}\| \dfrac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}\dfrac{\mathbf{b}}{\|\mathbf{b}\|}$$
\[\therefore \mathbf{p} = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|^2} \mathbf{b} \]
3. 正射影ベクトルの例題
3.1. 問題 1(ベクトルの正射影)
ベクトル \(\mathbf{a}\) を \(\mathbf{b}\) に正射影するためには、次の式を使います。
\[ \mathbf{p} = \frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{b} \cdot \mathbf{b}} \mathbf{b} \]
まず、内積を計算します。
\[ \mathbf{a} \cdot \mathbf{b} = 3 \times 1 + 4 \times 2 = 3 + 8 = 11 \]
次に、\(\mathbf{b} \cdot \mathbf{b} \) を計算します。
\[ \mathbf{b} \cdot \mathbf{b} = 1 \times 1 + 2 \times 2 = 1 + 4 = 5 \]
したがって、正射影ベクトルは
\[ \mathbf{p} = \frac{11}{5} \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} \frac{11}{5} \\ \frac{22}{5} \end{pmatrix} \]
これがベクトル \(\mathbf{a}\) をベクトル \(\mathbf{b}\) に正射影したベクトルです。
3.2. 問題 2 (垂直なベクトルの計算)
垂直なベクトル \(\mathbf{q}\) は、ベクトル \(\mathbf{a}\) と正射影ベクトル \(\mathbf{p}\) の差です。
\[ \mathbf{q} = \mathbf{a} – \mathbf{p} \]
\[ \mathbf{q} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} – \begin{pmatrix} \frac{11}{5} \\ \frac{22}{5} \end{pmatrix} = \begin{pmatrix} 3 – \frac{11}{5} \\ 4 – \frac{22}{5} \end{pmatrix} \]
\[ \mathbf{q} = \begin{pmatrix} \frac{4}{5} \\ -\frac{2}{5} \end{pmatrix} \]
したがって、ベクトル \(\mathbf{a}\) と正射影ベクトル \(\mathbf{p}\) の間に垂直なベクトル \(\mathbf{q}\) は
\[ \mathbf{q} = \begin{pmatrix} \frac{4}{5} \\ -\frac{2}{5} \end{pmatrix} \]
です。