線分の黄金比と黄金比の性質、関係式について

1. 黄金比とは?
黄金比と聞いて、あなたは何を思い浮かべますか?
その美しい比率は、古代ギリシャのパルテノン神殿や、現代におけるアップルのロゴなど、歴史と現代を超えてさまざまなデザインに使われています。この黄金比は、私たちの身の回りに多く存在し、どこか心地よく感じる形やデザインの背後にあります。では、黄金比とは具体的に何を指すのでしょうか?
例えば、線分$AB$を点$C$で分割したとします。このとき、線分全体$AB$の長さが、$AC$と$BC$の長さの比を次の関係式で満たすとき、この比率$\varphi$(ファイ)を黄金比と呼びます。
$$\dfrac{AB}{AC} = \dfrac{AC}{BC} = \varphi$$
具体的なイメージとして、$AB$が$AC$と$BC$に分かれる様子を図に示すと、次のような形になります。
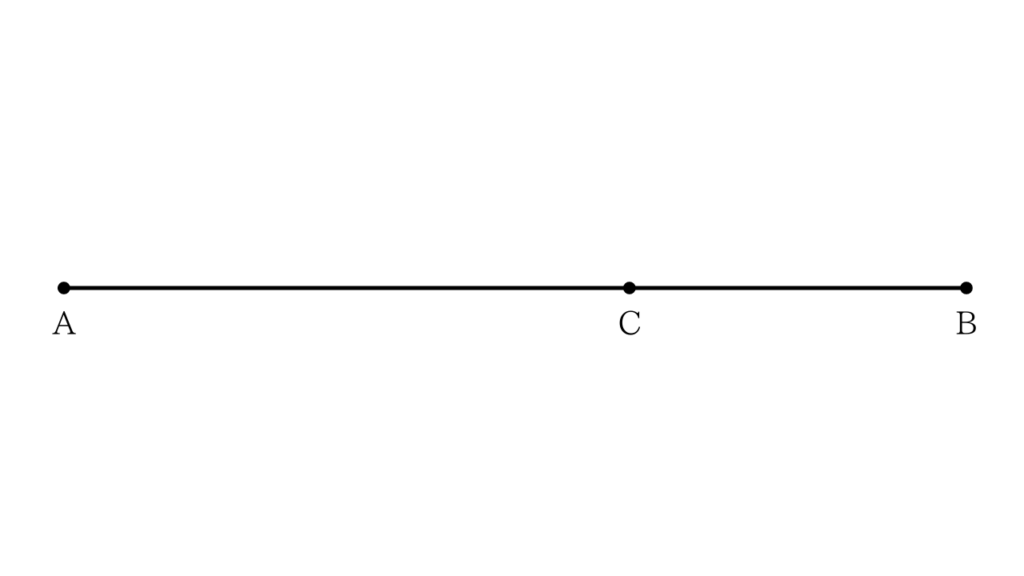
$$\varphi = \dfrac{1 + \sqrt{5}}{2}$$
ここで、黄金比$\varphi$の計算方法について詳しく見ていきましょう。
1.1. 黄金比$\varphi$の計算方法
線分$AB$の長さを$X+x$とし、$AC = X$、$BC = x$とおくと、次の式が成り立ちます。
$$\dfrac{AC}{AB} = \dfrac{BC}{AC} = \varphi$$
これを式にすると、
$$\dfrac{X + x}{X} = \dfrac{X}{x}$$
両辺を整理すると、
$$X^2 = Xx + x^2$$
この式をさらに簡単にするため、両辺を$x^2$で割り、$\dfrac{X}{x} = \varphi$に代入すると、
$$\varphi^2 = \varphi + 1$$
この式を解くと、次の二次方程式が得られます。
$$\varphi^2 – \varphi – 1 = 0$$
この二次方程式を解の公式で解くと、
$$\varphi = \dfrac{1 \pm \sqrt{5}}{2}$$
ここで、$\varphi > 0$なので、正の解を選び、最終的に
$$\varphi = \dfrac{1 + \sqrt{5}}{2}$$
2. 黄金比$\varphi$の性質
黄金比$\varphi$には、いくつかの興味深い性質があります。ここでは、そのうちのいくつかを紹介します。
$$\begin{align*} \varphi^2 &= \varphi + 1 \\ \dfrac{1}{\varphi} &= \varphi – 1 = \dfrac{\sqrt{5} – 1}{2} \\ \varphi + \dfrac{1}{\varphi} &= \sqrt{5} \\ \varphi^2 + \dfrac{1}{\varphi^2} &= 3 \end{align*}$$
これらの性質について、1つずつ計算して確認していきましょう。
2.1. 2番目の性質:$\dfrac{1}{\varphi} = \varphi – 1$の計算
まず、$\varphi^2 = \varphi + 1$の両辺に$\dfrac{1}{\varphi}$をかけます。
$$\varphi = 1 + \dfrac{1}{\varphi}$$
この式から、$\dfrac{1}{\varphi}$を求めると、
$$\dfrac{1}{\varphi} = \varphi – 1$$
ここに、先ほど求めた$\varphi = \dfrac{1 + \sqrt{5}}{2}$を代入すると、
$$\dfrac{1}{\varphi} = \dfrac{1 + \sqrt{5}}{2} – 1 = \dfrac{\sqrt{5} – 1}{2}$$
これで、2番目の性質が確認できました。
2.2. 3番目の性質:$\varphi + \dfrac{1}{\varphi} = \sqrt{5}$の計算
次に、2番目の性質と$\varphi = \dfrac{1 + \sqrt{5}}{2}$を用いて、$\varphi + \dfrac{1}{\varphi}$を計算します。
$$\varphi + \dfrac{1}{\varphi} = \dfrac{1 + \sqrt{5}}{2} + \dfrac{\sqrt{5} – 1}{2} = \dfrac{\sqrt{5} + \sqrt{5}}{2} = \sqrt{5}$$
このようにして、3番目の性質が成り立つことがわかります。
2.3. 4番目の性質:$\varphi^2 + \dfrac{1}{\varphi^2} = 3$の計算
最後に、3番目の性質を使って、この式の両辺を2乗します。
$$\left(\varphi + \dfrac{1}{\varphi}\right)^2 = \left(\sqrt{5}\right)^2 = 5$$
この式を展開すると、
$$\varphi^2 + 2 + \dfrac{1}{\varphi^2} = 5$$
ここから、
$$\varphi^2 + \dfrac{1}{\varphi^2} = 3$$
となり、4番目の性質が確認できました。



