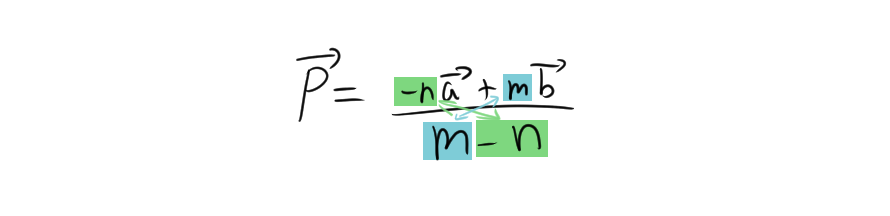外分点の位置ベクトルとは？導出と例題について

はるか

外分点は、内分と違って、線分を延長したところにある点。

ふゅか

そうそう！線分を「外に分ける」って感じよね。外分の位置ベクトルを求めるとき、比の扱いがちょっと変わるのがポイントよ！

はるか

式もマイナスが入っててややこしいけど、慣れれば単純。

1. 外分点の位置ベクトル

1.1. 外分点の位置ベクトルの対応関係

1.2. 外分点の位置ベクトルの導出

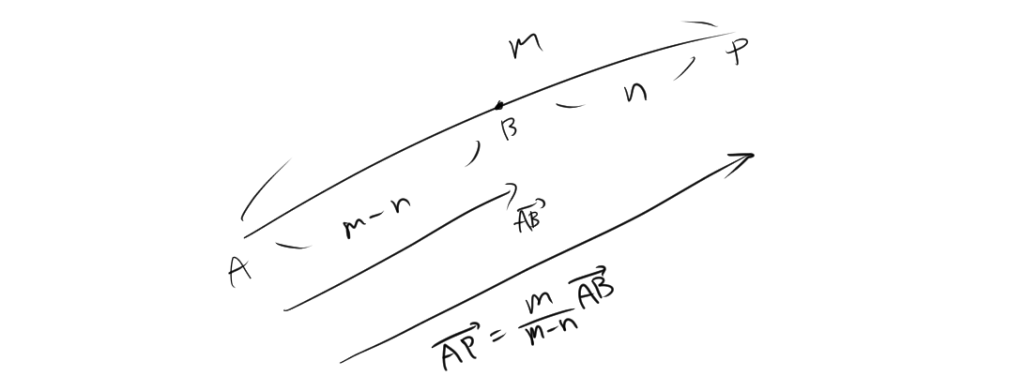
まず、点 $P$ が線分 $AB$ を外分する点であると考えます。点 \( A \)、\( B \)、および \( P \) への位置ベクトルを \(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{p}\) とします。ベクトル $\overrightarrow{OP}$ は、$\overrightarrow {OP} = \overrightarrow{OA}+\overrightarrow{AP}$より、

\[ \overrightarrow{p} = \overrightarrow{a} +\overrightarrow{AP}\]

ここで、線分の比より、$\overrightarrow{AP}=\frac{m}{m-n}\overrightarrow{AB}$となるので、

\[ \overrightarrow{p} = \overrightarrow{a} +\frac{m}{m-n}\overrightarrow{AB}\]

次に、ベクトル $\overrightarrow{AB}$ は、$\overrightarrow{AB} = \overrightarrow{b}-\overrightarrow{a}$より、

$$\begin{align*} \overrightarrow{p} &= \overrightarrow{a} + \frac{m}{m-n}(\overrightarrow{b}-\overrightarrow{a}) \\ &= \frac{m-n}{m-n}\overrightarrow{a} + \frac{m}{m-n}(\overrightarrow{b}-\overrightarrow{a}) \\ &= \frac{-n\overrightarrow{a} + m\overrightarrow{b}}{m-n} \end{align*}$$

1.3. 内分点の位置ベクトルを利用した導出

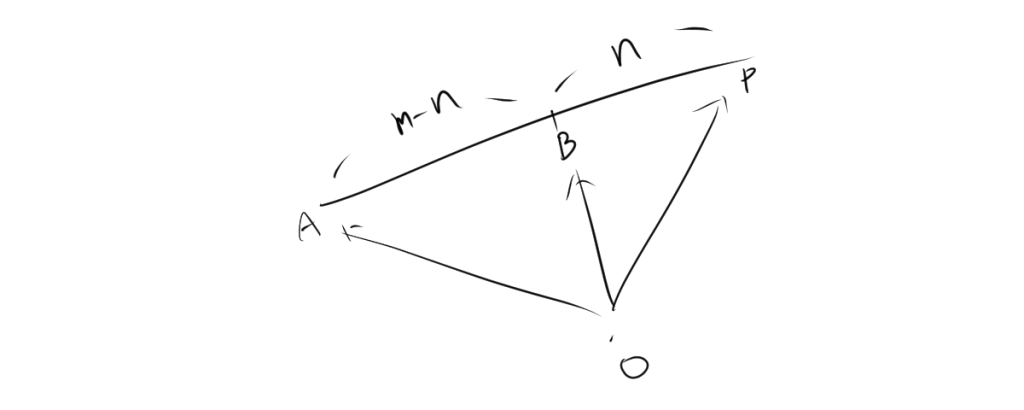APをBが内分していると考えると、内分点の位置ベクトルより、

$$\overrightarrow{b}=\frac{n\overrightarrow{a}+(m-n)\overrightarrow{p}}{m-n+n}$$

となるので、

$$\begin{align*} (m-n)\overrightarrow{p} &=-n\overrightarrow{a}+m\overrightarrow{b} \\ \overrightarrow{p}&= \frac{-n\overrightarrow{a} + m\overrightarrow{b}}{m-n}\end{align*}$$

1.4. 具体例

例えば、点 \( A(1, 2) \) と点 \( B(5, 6) \) の間にある点 \( P \) が、線分 \( AB \) を \( 2:1 \) の比で外分する場合を考えます。点 \( A \) の位置ベクトルを \(\overrightarrow{a} = (1, 2)\)、点 \( B \) の位置ベクトルを \(\overrightarrow{b} = (5, 6)\) とします。

点 \( P \) の位置ベクトル \(\overrightarrow{p}\) は次のように求められます。

\[ \overrightarrow{p} = \frac{-1 \cdot \overrightarrow{a} + 2 \cdot \overrightarrow{b}}{2 – 1} = \frac{-1 \cdot (1, 2) + 2 \cdot (5, 6)}{1} \]

これを計算すると、

\[ \overrightarrow{p} = (-1 + 10, -2 + 12) = (9, 10) \]

つまり、点 \( P \) の位置ベクトルは \(\overrightarrow{p} = (9, 10)\) となります。

2. 例題

2.1. 例題1

まず、外分点の位置ベクトルを計算してみましょう。

\[ \vec{p} = \frac{-2\vec{a} + 3\vec{b}}{3 – 2} \]

それぞれの位置ベクトルを代入します。

\[ \vec{p} = \frac{-2(2, 3) + 3(8, 5)}{1} \]

次に各成分を計算します。

\[ \vec{p} = \frac{(-4, -6) + (24, 15)}{1} \]

\[ \vec{p} = \frac{(20, 9)}{1} = (20, 9) \]

外分点 \( P \) の位置ベクトルは \((20, 9)\) です。

2.2. 例題2

まず、与えられた情報を式に代入します。

\[ (20, 9) = \frac{-2\vec{a} + 3(8, 5)}{3 – 2} \]

分母を計算すると、

\[ (20, 9) = -2\vec{a} + 3(8, 5) \]

次に、各成分ごとに等式を展開します。

\[ (20, 9) = (-2x + 24, -2y + 15) \]

したがって、

$$\begin{align*} (-2x + 24, -2y + 15) &= (20, 9) \\ (-2x, -2y) &= (-4, -6) \\ (x, y) &= (2, 3) \end{align*}$$

点 \( A \) の位置ベクトルは \((2, 3)\) です。