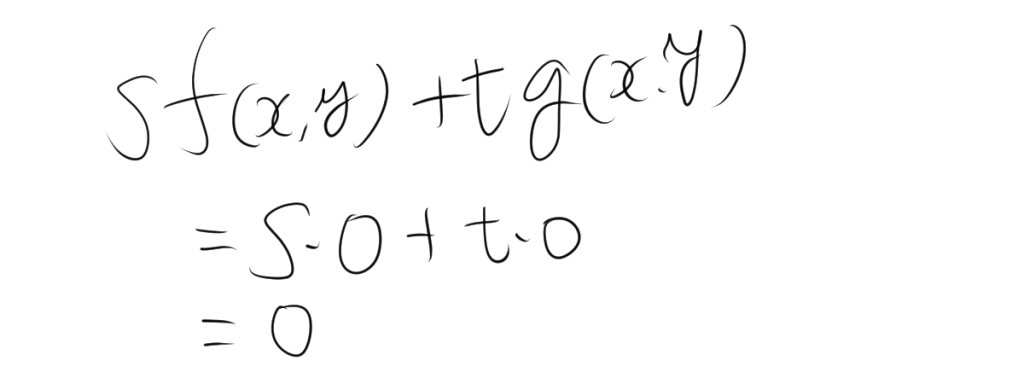【図解】束と証明、交点と例題について

1. 束
\[ s f(x,y) + t g(x,y) = 0 \]
が表す図形は、 $ f(x,y) = 0 $ と $g(x,y) = 0$が表す図形の交点が存在するとき、交点の全て含む図形になります。
- 束とは、2つの図形(通常は曲線や直線)の交点をすべて含む図形を表すものです。
- 英語だと、pencilです。群にかかわってくる束(lattice)とはまた、別です。
1.1. なぜ和が0になるのか
一言でいうと、「0に何をかけても0でしょ」ということです。$ f(x,y) = 0 $ と $g(x,y) = 0$は0であるので。
2. 証明
束が交点を含むのか証明してみましょう。
交点を \((p, q)\) とすると、これに対して \(f(p, q) = 0\) かつ \(g(p, q) = 0\) が成立します。よって、\((p, q)\) は \(f(x, y) = 0\) と \(g(x, y) = 0\) の交点です。
まず、与えられた式
\[ s f(x, y) + t g(x, y) = 0 \]
について考えます。この式は、\(s\) と \(t\) が少なくとも一つ 0 でないときに成り立つものとします。
\((p, q)\) は \(f(x, y) = 0\) と \(g(x, y) = 0\) の交点であるので、これを上記の式に代入すると
\[ s f(p, q) + t g(p, q) = s \cdot 0 + t \cdot 0 = 0 \]
が成り立ちます。したがって、交点\((p, q)\) は必ず \(s f(x, y) + t g(x, y) = 0\) を満たし、交点が複数ある場合は同様の議論をしたらよい。つまり、交点は必ずこの式が表す図形上に含まれることが示されました。
3. 例題
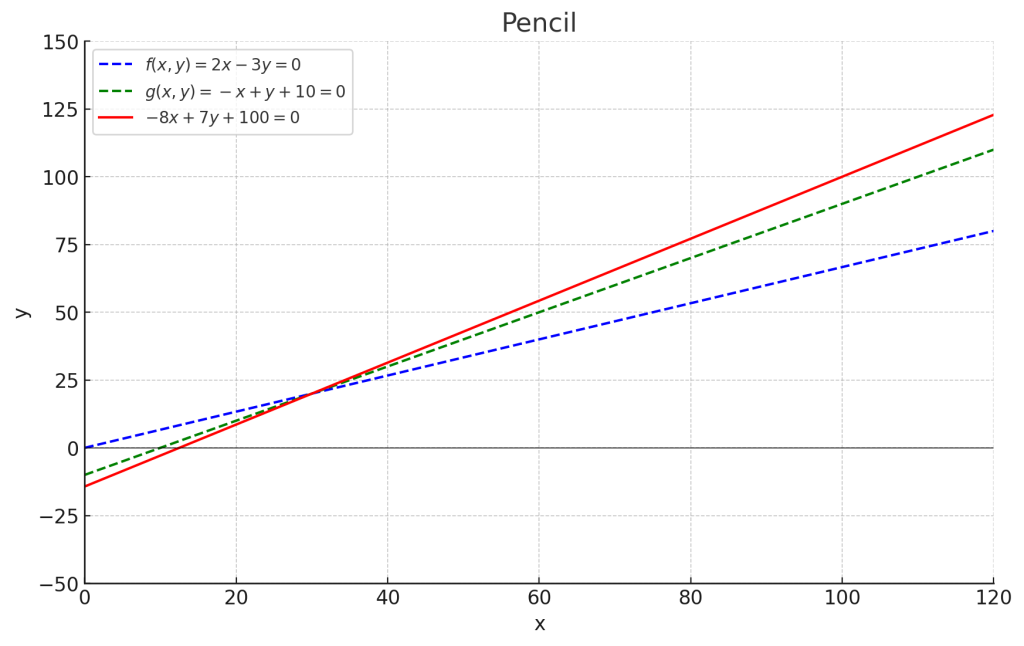
3.1. 例題1 (直線と直線)
- \( f(x, y) = 2x – 3y = 0 \)
- \( g(x, y) = -x + y +10= 0 \)
これらの直線が交わる点と点 \((100, 100)\) を通る直線の方程式を求めなさい
s と t が実数で、少なくとも一つが0でないとしたとき、
\[ s(2x-3y) + t(-x + y +10) = 0 \]
とすると、点 \((100, 100)\) を通るので、
$$\begin{align*} -100s + 10t &= 0 \\ t &= 10s \end{align*}$$
s と t は少なくとも一つが0でないので、$s=1,t=10$とすると、
$$\begin{align*} 2x – 3y – 10x + 10y + 100 &= 0 \\ -8x + 7y + 100 &= 0 \end{align*}$$
この直線の束を図にすると、
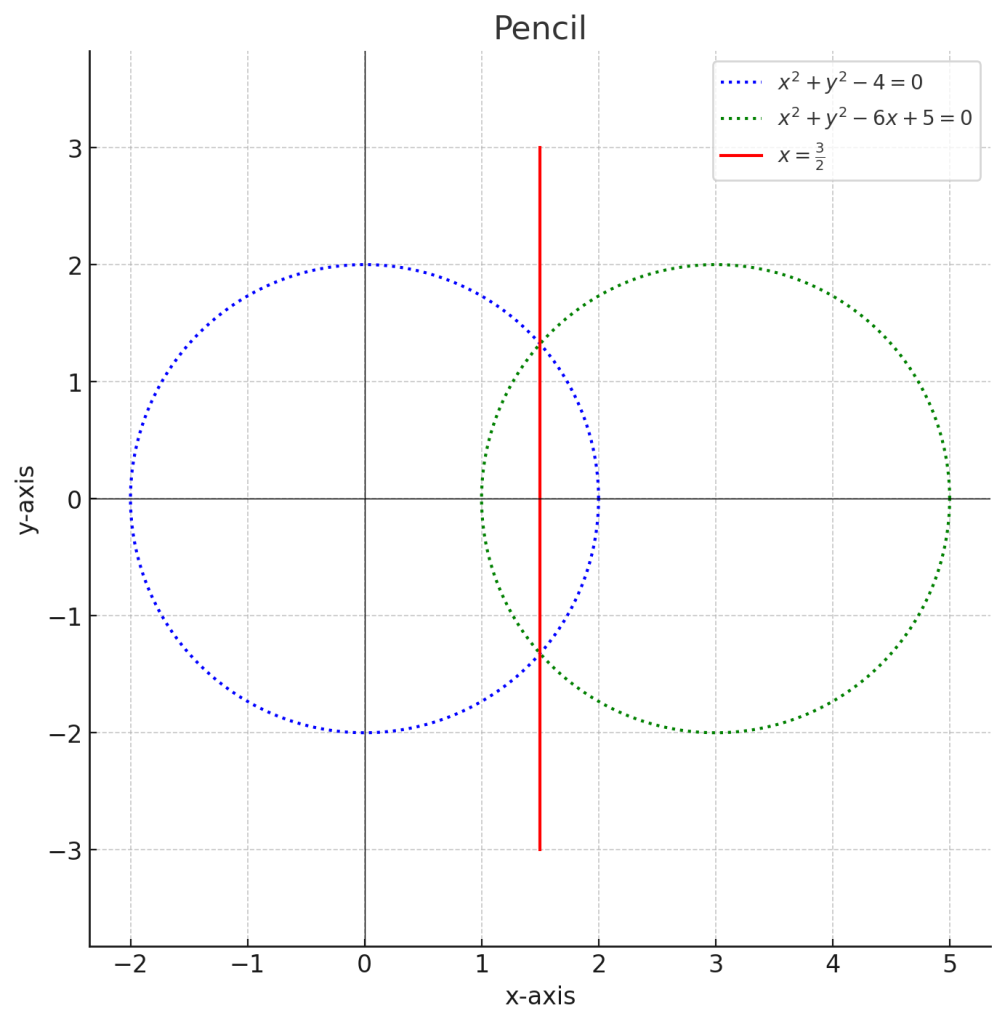
3.2. 例題2 (円と円)
直線の束は次の式で表されます。
\[ s (x^2 + y^2 – 4) + t (x^2 + y^2 – 6x + 5) = 0 \]
$s$ と $t$ は実数であり、少なくとも一方が0でないとします。$x^2$と$y^2$の項を消したいので、$s=1,t=-1$とすると、
$$\begin{align*} (x^2 + y^2 – 4) – (x^2 + y^2 – 6x + 5) &= 0 \\ -4 + 6x – 5 &= 0 \\ x &= \frac{3}{2} \end{align*}$$
この円の束を図にすると、