多項式、単項式とは?意味と具体例について

はるか
単項式は、項が1つだけの式。
ふゅか
うん!例えば、$9000000x^{654455}$みたいなものね♪ 単純な形だけど、基礎になる重要な式よ!
1. 単項式
単項式とは、定数と変数の積で表される1つの項から成る式のことです。多項式の中でも、項が1つしかない特別な場合を指します。具体的には、次のように表されます。
\[ ax^n \]
ここで、
- \( a \) は定数(係数)
- \( x \) は変数
- \( n \) は非負の整数で、変数のべき乗を表します
1.1. 単項式の例
例えば、以下のものは単項式です。
- \( 5x^3 \)
- \( -7x \)
- \( 2 \)(これは変数を含まない単項式)
単項式は複雑な構造を持たず、簡潔で基本的な式ですが、多項式の構成要素にもなります。
1.2. 多項式の係数
単項式の係数とは、単項式における変数に掛けられている定数部分を指します。たとえば、単項式が次のように表されているとき。
\[ ax^n \]
この式において、\( a \) が係数です。
多項式の係数の具体的な例を挙げると、
- 単項式 \( 5x^2 \) の係数は \( 5 \) です。
- 単項式 \( -3x^3 \) の係数は \( -3 \) です。
- 単項式 \( x^4 \) の係数は \( 1 \) です(これは \( 1x^4 \) と同じです)。
- 単項式 \( -x \) の係数は \( -1 \) です。
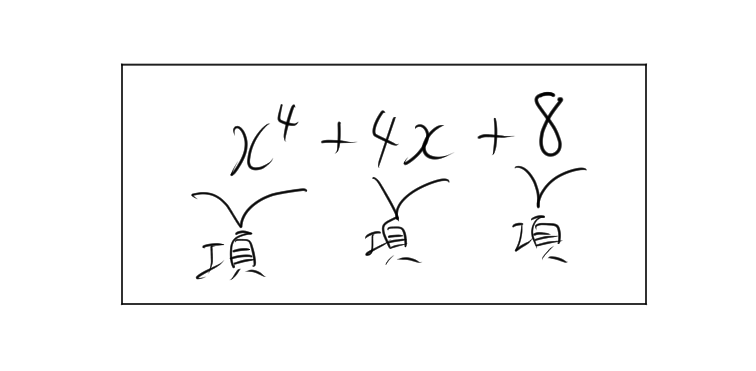
2. 多項式とは
多項式とは、定数と変数を使って作られた式で、変数のべき乗とそれに定数を掛けた項の和として表されます。一般的には次の形で表されます。
\[ P(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 \]
ここで、
- \( x \) は変数
- \( a_n, a_{n-1}, \ldots, a_1, a_0 \) は定数(係数)
- \( n \) は非負の整数で、多項式の「次数」を表します。例えば、最高のべき乗(\( x^n \))の指数が次数です。
- 多項式は整式とも呼ばれる。
はるか
多項式は単項式の和で表される。
2.1. 多項式の例
多項式の例としては、次のようなものがあります。
- 一次多項式: \( 3x + 2 \)
- 二次多項式: \( x^2 + 2x + 1 \)
- 三次多項式: \( 2x^3 – 5x + 7 \)
また、項数が1つの場合は「単項式」、2つ以上の場合は「多項式」とも呼ばれます。
余談になりますが、多項式全体の集合を線形空間で定義することができます。
PR