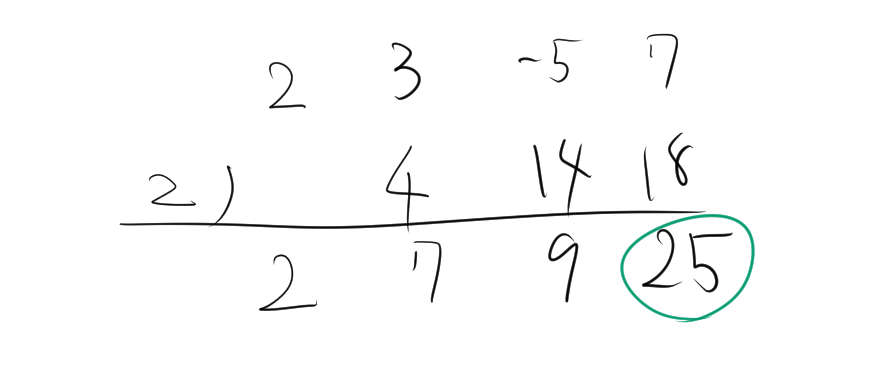剰余の定理の証明と計算、3つの例題について

1. 剰余の定理とは
剰余の定理は、多項式の除法に関連する定理です。
1.1. 剰余の定理
\( f(x) \) を \( x – a \) で割ったときの余りは、\( f(a) \) に等しい。
1.2. 剰余の定理の例
例えば、次の多項式を考えます。
\[ f(x) = 2x^3 + 3x^2 – 5x + 7 \]
これを \( x – 2 \) で割るとします。この場合、剰余の定理によって、余りは \( f(2) \) で求められます。
\[ f(2) = 2(2)^3 + 3(2)^2 – 5(2) + 7 = 16 + 12 – 10 + 7 = 25 \]
したがって、余りは \( 25 \) となります。
組立除法で、余りが正しいか確認すると次のようになる。
2. 剰余の定理の証明
2.1. 証明
多項式 \( f(x) \) を一次式 \( x – a \) で割ると、次のように書けます。
\[ f(x) = (x – a)q(x) + r \]
ここで、\( q(x) \) は商、\( r \) は余りです。そして、余り \( r \) は一次式 \( x – a \) で割るため、\( r(x) \) は定数になります。したがって、\( r(x) = r \) です。
両辺に \( x = a \) を代入します。すると、
\[ f(a) = (a – a)q(a) + r \]
\[ f(a) = 0 \cdot q(a) + r \]
結果として、余り \( r \) は次のように求められます。
\[ r = f(a) \]
よって、剰余の定理が成り立つことが証明されました。つまり、多項式 \( f(x) \) を \( x – a \) で割ったときの余りは \( f(a) \) に等しいということです。
2.2. 補足
この剰余の定理は「因数定理」にもつながります。もし \( f(a) = 0 \) であれば、\( x – a \) は \( f(x) \) の因数であることがわかります。
3. 剰余の定理の例題
3.1. 例題 1:
剰余の定理より、\( f(2) \) を計算すれば余りが求められます。
\[ f(2) = 2^3 + 2 \cdot 2^2 – 5 \cdot 2 + 3 = 8 + 8 – 10 + 3 = 9 \]
したがって、余りは \( 9 \) です。
3.2. 例題 2:
剰余の定理を使うためには、\( f(-1) \) を計算します。
\[ f(-1) = 4(-1)^4 – 3(-1)^3 + (-1)^2 – 2(-1) + 5 = 4 + 3 + 1 + 2 + 5 = 15 \]
したがって、余りは \( 15 \) です。
3.3. 例題 3:
剰余の定理に従って、\( f(3) \) を計算します。
\[ f(3) = 2(3)^5 – 7(3)^4 + (3)^2 – 4(3) + 6 = 2 \cdot 243 – 7 \cdot 81 + 9 – 12 + 6 = 486 – 567 + 9 – 12 + 6 = -78 \]
したがって、余りは \( -78 \) です。