Popoviciuの不等式の意味と証明について

1. Popoviciuの不等式
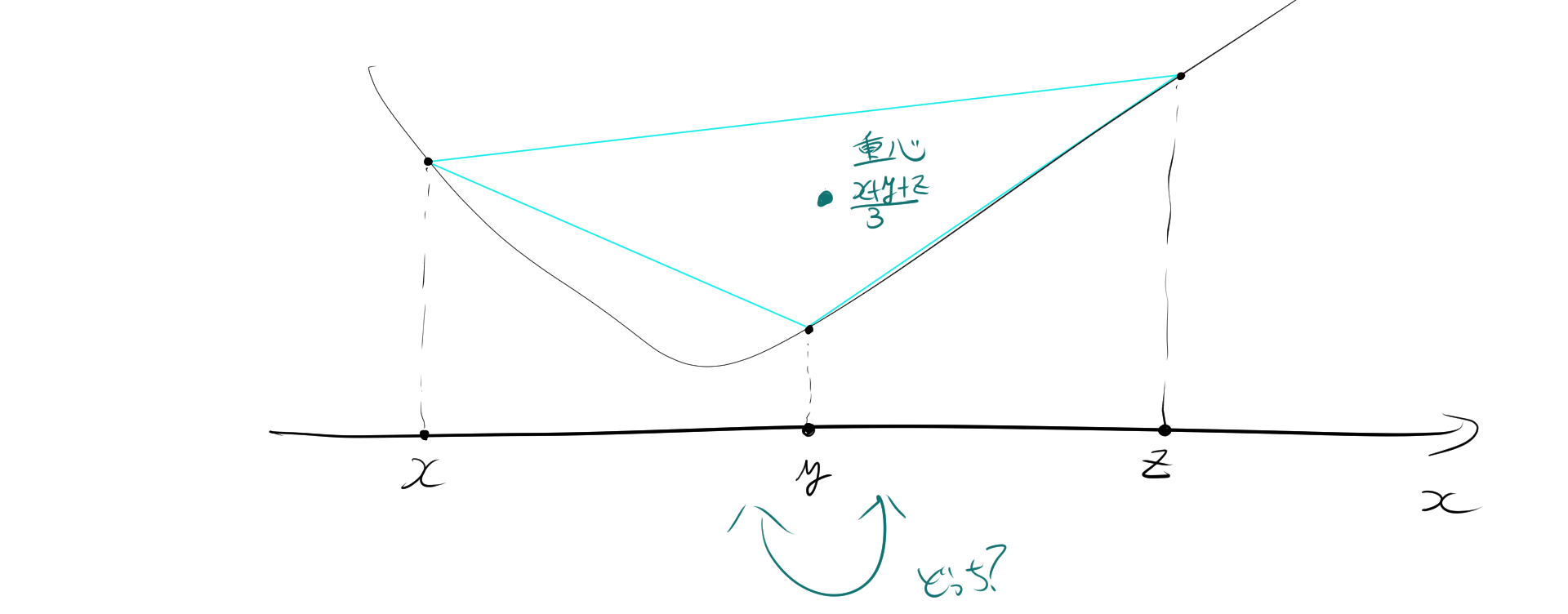
\(f\)を区間\(I\subset \mathbb{R}\)上で定義された凸関数とし、任意の\(x, y, z \in I\)に対して、以下の不等式が成り立ちます。
\[ f(x) + f(y) + f(z) + 3f\left(\frac{x+y+z}{3}\right) \leq 2f\left(\frac{x+y}{2}\right) + 2f\left(\frac{y+z}{2}\right) + 2f\left(\frac{z+x}{2}\right) \]
2. Jensenの不等式を利用した証明
凸関数とくれば、やっぱり外せないJensenの不等式を利用して証明してみましょう。
2.1. Jensenの不等式
Jensenの不等式とは、次のような不等式です。
凸関数 \( f(x) \) に対して、任意の実数 \( x_1, x_2, \ldots, x_n \) と非負の重み \( \lambda_1, \lambda_2, \ldots, \lambda_n \) が以下を満たすとします。
\[ \lambda_i \geq 0, \quad \sum_{i=1}^n \lambda_i = 1 \]
このとき、次の不等式が成り立ちます
\[ f\left( \sum_{i=1}^n \lambda_i x_i \right) \leq \sum_{i=1}^n \lambda_i f(x_i) \]
2.2. 証明
不等式の対称性から、一般性を失わないので、$x\leq y \leq z$の時を証明する。
Jensenの不等式より、
$$f\left(\frac{x}{2}+\frac{y}{2}\right) \geq \frac{f(x)}{2}+\frac{f(y)}{2}$$
したがって、
$$f(x)+f(y)\ \leq 2f\left(\frac{y+z}{2}\right)$$
となるので、
$$f(z)+3f\left(\frac{x+y+z}{3} \right) \leq 2f\left(\frac{y+z}{2}\right) + 2f\left(\frac{z+x}{2}\right)$$
を証明する。
証明は \( y \leq \frac{x+y+z}{3} \) の場合と \(\frac{x+y+z}{3} \leq y\) の場合に場合分けして行う。
ここでは \( y \leq \frac{x+y+z}{3} \) の場合を示す。もう一方の場合も同様に計算できる。
\[ \frac{x+y+z}{3} \leq \frac{x+z}{2} \leq z \quad \text{かつ}\quad \frac{x+y+z}{3} \leq \frac{y+z}{2} \leq z \]
また、\(\frac{x+z}{2}\) と \(\frac{y+z}{2}\) は共に重心\(\frac{x+y+z}{3}\) と \(x\) の間にある点である。したがって、ある \( s,t \in [0,1] \) が存在して
\[ \frac{x+z}{2} = s\frac{x+y+z}{3} + (1-s)z, \quad \frac{y+z}{2} = t\frac{x+y+z}{3} + (1-t)z \]
と書ける。
この2つを加えると
\[ \frac{x+z}{2} + \frac{y+z}{2} = (s+t)\frac{x+y+z}{3} + [2-(s+t)]z \]
左辺は \(\frac{x+y+2z}{2}\) であるから、
\[ \frac{x+y+2z}{2} = (s+t)\frac{x+y+z}{3} + [2-(s+t)]z \]
両辺から \(2z\) を引くため、右辺を整理する。
まず、\(\frac{x+y+2z}{2}-2z = \frac{x+y-2z}{2}\) である。一方、右辺は
\[ (s+t)\frac{x+y+z}{3} + [2-(s+t)]z – 2z = (s+t)\frac{x+y+z}{3} – (s+t)z \]
これを \((s+t)\) で括ると
\[ (s+t)\left(\frac{x+y+z}{3}-z\right) = (s+t)\frac{x+y-2z}{3} \]
よって
\[ \frac{x+y-2z}{2} = (s+t)\frac{x+y-2z}{3} \]
ここで \( x+y-2z \neq 0 \) であるので、
\[ s+t = \frac{3}{2} \]
\( f \) が凸であるから、\(\frac{x+z}{2}\) と \(\frac{y+z}{2}\) から Jensenの不等式を適用すると
\[ f\left(\frac{x+z}{2}\right) \leq s f\left(\frac{x+y+z}{3}\right) + (1-s)f(z), \] \[ f\left(\frac{y+z}{2}\right) \leq t f\left(\frac{x+y+z}{3}\right) + (1-t)f(z) \]
両辺を足して
\[ f\left(\frac{x+z}{2}\right) + f\left(\frac{y+z}{2}\right) \leq (s+t) f\left(\frac{x+y+z}{3}\right) + [2-(s+t)]f(z) \]
\( s+t = \frac{3}{2}\) より
\[ f\left(\frac{x+z}{2}\right) + f\left(\frac{y+z}{2}\right) \leq \frac{3}{2}f\left(\frac{x+y+z}{3}\right) +\frac{1}{2}f(z) \]
したがって、
$$f(z)+3f\left(\frac{x+y+z}{3} \right) \leq 2f\left(\frac{y+z}{2}\right) + 2f\left(\frac{z+x}{2}\right)$$
3. karamataの不等式を利用した証明
Jensenの不等式だけでなく、凸関数の不等式であるkaramataの不等式でも、証明を行うことができます。
3.1. karamataの不等式
Karamataの不等式は、凸関数 \( f \) と二つの列 \( a=(a_1,\dots,a_n) \), \( b=(b_1,\dots,b_n) \) に関して「\( a \) が \( b \) よりも偏りが大きい(majorize する)」、すなわち\[ [a] \succ [b] \] が成り立つとき、次の不等式が成り立ちます。
\[ f(a_1) + \cdots + f(a_n) \geq f(b_1) + \cdots + f(b_n) \] (\( f \) が凸の場合)。
3.2. 証明
不等式の対称性から、一般性を失わないので、$x\leq y \leq z$かつ\( y \geq \frac{x+y+z}{3} \)の時を証明する。
このとき、次の不等式が成り立つ。
\[ \frac{x+y+z}{3} \geq \frac{x+z}{2} \geq x \quad \text{かつ}\quad \frac{x+y+z}{3} \geq \frac{y+z}{2} \geq x \]
6つの値の比較
以下の2つの6つの数列を考える。
\[ a = \left(z,\;y,\;\frac{x+y+z}{3},\;\frac{x+y+z}{3},\;\frac{x+y+z}{3},\;x\right) \]
\[ b = \left(\frac{y+z}{2},\;\frac{y+z}{2},\;\frac{z+x}{2},\;\frac{z+x}{2},\;\frac{x+y}{2},\;\frac{x+y}{2}\right) \]
ここで、いずれも要素の和は同じであることが分かる。実際、
\[ \sum_{i=1}^6 a_i = z + y + (x+y+z) + x = 2(x+y+z), \] \[ \sum_{i=1}^6 b_i = 2\frac{y+z}{2} + 2\frac{z+x}{2} + 2\frac{x+y}{2} = (y+z) + (z+x) + (x+y) = 2(x+y+z). \]
よって \(\sum a_i = \sum b_i\) である。
偏りの比較
次に、\( a \) と \( b \) を大きい方から並べたときの「偏り」を比較する。
\( a \) の部分和
\( a = \left(z, y, \frac{x+y+z}{3}, \frac{x+y+z}{3}, \frac{x+y+z}{3}, x\right) \) に基づき計算します:
\[ \begin{aligned} S_1^a &= z, \\ S_2^a &= z + y, \\ S_3^a &= z + y + \frac{x+y+z}{3}, \\ S_4^a &= z + y + 2 \cdot \frac{x+y+z}{3}, \\ S_5^a &= z + y + 3 \cdot \frac{x+y+z}{3} = z + y + x + y + z, \end{aligned} \]
各部分和を整理して書き下します
\[ \begin{aligned} S_1^a &= z, \\ S_2^a &= z + y, \\ S_3^a &= z + y + \frac{x+y+z}{3}, \\ S_4^a &= z + y + \frac{2(x+y+z)}{3}, \\ S_5^a &= 2z + 2y + x \end{aligned} \]
\( b \) の部分和
\( b = \left(\frac{y+z}{2}, \frac{y+z}{2}, \frac{z+x}{2}, \frac{z+x}{2}, \frac{x+y}{2}, \frac{x+y}{2}\right) \) に基づき計算します。
\[ \begin{aligned} S_1^b &= \frac{y+z}{2}, \\ S_2^b &= \frac{y+z}{2} + \frac{y+z}{2} = y + z, \\ S_3^b &= y + z + \frac{z+x}{2}, \\ S_4^b &= y + z + \frac{z+x}{2} + \frac{z+x}{2} = y + z + z + x, \\ S_5^b &= y + z + z + x + \frac{x+y}{2} \end{aligned} \]
各部分和を整理して書き下します: \[ \begin{aligned} S_1^b &= \frac{y+z}{2}, \\ S_2^b &= y + z, \\ S_3^b &= y + z + \frac{z+x}{2}, \\ S_4^b &= 2z + y + x, \\ S_5^b &= 2z + 2y + x \end{aligned} \]
\( a \) と \( b \) の部分和の比較
| 項番 | \( S_i^a \) | \( S_i^b \) | 比較 |
|---|---|---|---|
| 1 | \( z \) | \( \frac{y+z}{2} \) | \( z \geq \frac{y+z}{2} \) (成り立つ) |
| 2 | \( z + y \) | \( y + z \) | \( z + y = y + z \) (成り立つ) |
| 3 | \( z + y + \frac{x+y+z}{3} \) | \( y + z + \frac{z+x}{2} \) | 比較必要 |
| 4 | \( z + y + \frac{2(x+y+z)}{3} \) | \( y + z + z + x \) | 比較必要 |
| 5 | \( 2z + 2y + x \) | \( 2z + 2y + x \) | 等しい |
| 6 | \( 2z + 2y + 2x \) | \( 2z + 2y + 2x \) | 等しい |
\( S_3^a \) と \( S_3^b \) の比較け
- \( S_3^a \): \[ S_3^a = z + y + \frac{x+y+z}{3}. \]
- \( S_3^b \): \[ S_3^b = y + z + \frac{z+x}{2}. \]
- 比較 \( S_3^a \geq S_3^b \): 両辺を引き算すると、不等式の条件より、 \[ S_3^a – S_3^b = \frac{x+y+z}{3} – \frac{z+x}{2}\geq 0\]
\( S_4^a \) と \( S_4^b \) の比較
- \( S_4^a \): \[ S_4^a = z + y + \frac{2(x+y+z)}{3} \]
- \( S_4^b \): \[ S_4^b = y + z + z + x \]
- 比較 \( S_4^a \geq S_4^b \): 両辺を引き算すると、 \[ S_4^a – S_4^b = \frac{2(x+y+z)}{3} – (z + x) \] 共通の分母 \(3\) を取ると \[ S_4^a – S_4^b = \frac{2(x+y+z) – 3(z+x)}{3} = \frac{2y – z – x}{3}\]\( y \geq \frac{x+y+z}{3} \)なので \( 2y \geq z + x \) が成立し、したがって \( S_4^a \geq S_4^b \) が成立。
全ての部分和で \( S_i^a \geq S_i^b \) が成り立ち、また総和が等しいため、 \[ [a] \succ [b] \] します。
Karamataの不等式の適用
\( f \) が凸であり、\( a \succ b \) が成り立つとき、Karamataの不等式より \[f(x) + f(y)+f(z) + f\left(\frac{x+y+z}{3}\right) +f\left(\frac{x+y+z}{3}\right) +f\left(\frac{x+y+z}{3}\right) \geq f\left(\frac{y+z}{2}\right)+f\left(\frac{y+z}{2}\right)+f\left(\frac{z+x}{2}\right)+f\left(\frac{z+x}{2}\right)+f\left(\frac{x+y}{2}\right)+f\left(\frac{x+y}{2}\right) \] が成り立つので、
\[ f(x) + f(y) + f(z) + 3f\left(\frac{x+y+z}{3}\right) \leq 2f\left(\frac{x+y}{2}\right) + 2f\left(\frac{y+z}{2}\right) + 2f\left(\frac{z+x}{2}\right) \]