位置ベクトルとは?内分と外分、重心ベクトルの一覧

ふゅか
位置ベクトルって何だったか覚えてる?点の位置を示すものだよね!
はるか
そう、原点からの距離と方向で示すベクトル。
1. 位置ベクトルとは
位置ベクトルは、平面や空間内の点の位置を原点からの距離と方向で表現するベクトルです。つまり、基準となる点(原点)から特定の点までを結ぶベクトルとしてあらわされます。
1.1. 位置ベクトルの例
例えば、2次元の座標平面で点 \( P(x, y) \) の位置ベクトルは次のように表現されます。
\[ \overrightarrow{OP} = (x, y) \]
1.2. 位置ベクトルの応用
2点 \( A \) と \( B \) の位置ベクトルがそれぞれ \(\overrightarrow{a}\) と \(\overrightarrow{b}\) であるとき、ベクトル \(\overrightarrow{AB}\) は次のように求めることができます。
\[ \overrightarrow{AB} =\overrightarrow{OB}- \overrightarrow{OA}= \overrightarrow{b} – \overrightarrow{a} \]
$\overrightarrow{AB}= \overrightarrow{OB}- \overrightarrow{OA}$はベクトルの分解を参考。
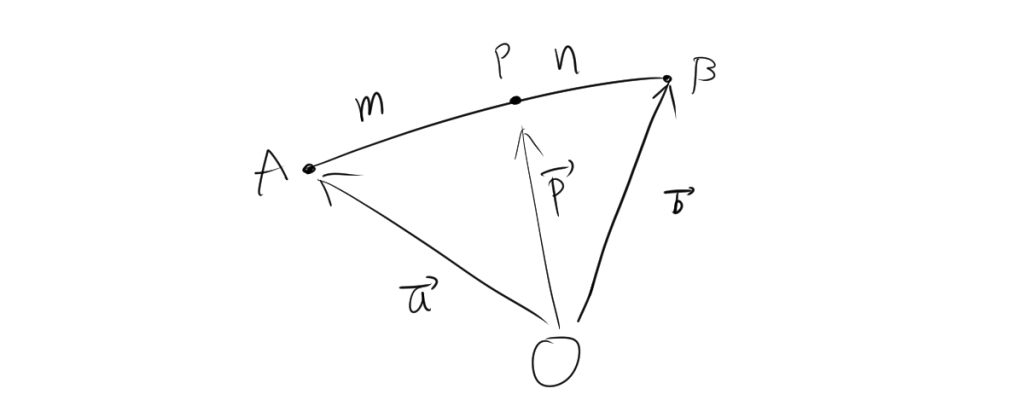
2. 内分点の位置ベクトルとは
点 \( P \) が線分 \( AB \) を \( m:n \) の比で内分するとき、原点からそれぞれの点 \( A \)、\( B \)、および \( P \) への位置ベクトルを \(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{p}\) としたとき、
\[ \overrightarrow{p} = \frac{n \overrightarrow{a} + m \overrightarrow{b}}{m + n} \]
詳しくは次の記事で解説しています。
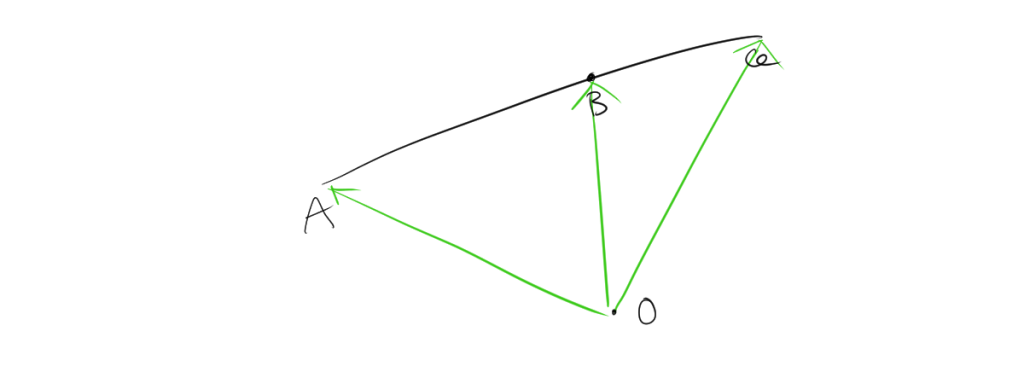
3. 外分点の位置ベクトルとは
点 \( P \) が線分 \( AB \) を \( m:n \) の比で外分するとき、原点からそれぞれの点 \( A \)、\( B \)、および \( Q \) への位置ベクトルを \(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{q}\) としたとき、次の関係式が成り立ちます。
\[ \overrightarrow{q} = \frac{-n \overrightarrow{a} + m \overrightarrow{b}}{m – n} \]
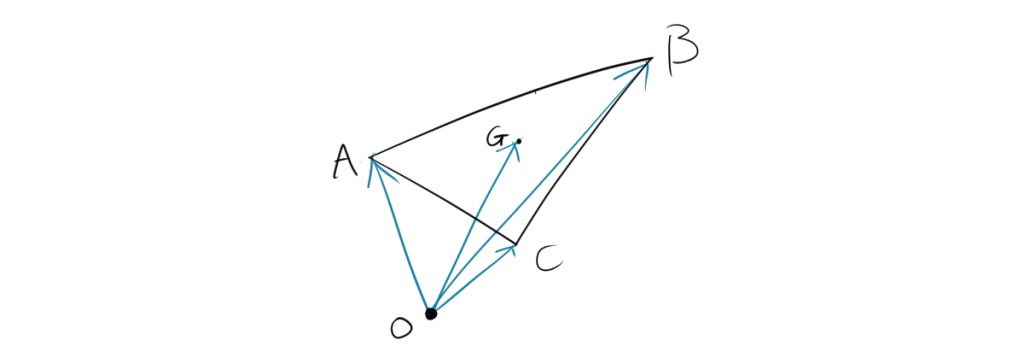
4. 重心の位置ベクトル
三角形の頂点を \( A \), \( B \), \( C \) とし、それぞれの位置ベクトルを \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) とします。重心 \( G \) の位置ベクトル \(\vec{g}\) は次の式で表されます。
\[ \vec{g} = \frac{\vec{a} + \vec{b} + \vec{c}}{3} \]
ふゅか
重心の位置ベクトルも面白いよね!三角形の頂点 \( A \), \( B \), \( C \) があったら、重心 \( G \) の位置ベクトルは…
はるか
\(\vec{g} = \frac{\vec{a} + \vec{b} + \vec{c}}{3}\)。
ふゅか
三つの頂点の平均を取る感じだね。
PR