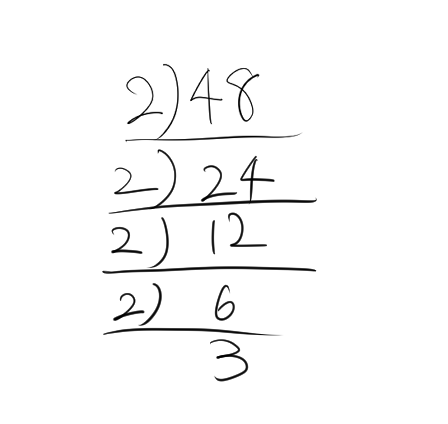素因数分解とは?素因数分解のコツと例題について

1. 素因数分解
素因数分解とは、自然数をそれ以上分解できない素数の積として表すことを指します。具体的には、ある自然数 \( n \) が与えられたとき、その数を素数(1とその数自身以外に約数を持たない数)だけで構成される形に分解することを素因数分解と言います。
例えば、次のような素因数分解ができます。
- \( 12 \) の素因数分解は \( 2^2 \times 3 \)
- \( 30 \) の素因数分解は \( 2 \times 3 \times 5 \)
このように、与えられた自然数を素数の積として表すことで、数の構造を理解しやすくするための基本的な手法です。
素因数分解は次のように書かれることがあります。
2. 素因数分解のコツ
2.1. 倍数の判定法を利用
まず、素因数分解の基本的な手順として、対象の数がいくつかの小さい素数の倍数かどうかを判定する方法を利用します。特に、2や3、5などの小さい素数についての倍数判定は最低限押さえておくべきでしょう。
- 2の倍数: 偶数であれば2の倍数です。
- 3の倍数: 各桁の数字を合計し、その合計が3の倍数であれば、その数も3の倍数です。
- 5の倍数: 数字の最後の桁が0または5であれば、その数は5の倍数です。
- 9の倍数: 各桁の数字を合計し、その合計が9の倍数であれば、その数も9の倍数です。
- 11の倍数: 奇数桁と偶数桁の数字を合計し、その差が11の倍数であれば、その数も11の倍数です。
このような倍数判定法を駆使することで、素因数分解のスピードを大幅に上げることができます。
2.2. $\sqrt{n}$まで計算
次に、素因数分解を効率よく行うための重要なポイントは、平方根までの素数で割り算することです。具体的に、任意の整数$n$の素因数を求める際には、$n$の平方根$\sqrt{n}$までの範囲で素数を確認すれば十分です。
たとえば、100を素因数分解する場合、$\sqrt{100} = 10$ですので、2から10までの素数(2、3、5、7)で割り算を試みるだけで、その数の素因数が得られます。これにより、不要な計算を減らし、より効率的に素因数分解を進めることができます。
2.3. 図を利用
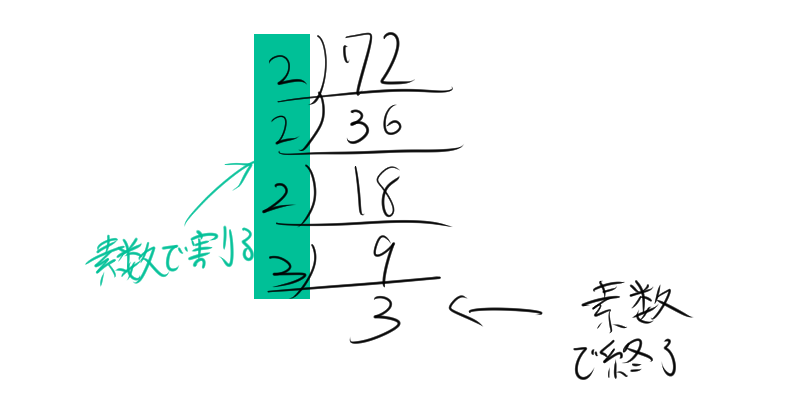
素因数分解を簡単に行うために、次のような図を使うことができます。ここでは、72を例にして説明しましょう。
まず、72を素数で順番に割っていきます。以下の図のように、72からスタートし、割った結果の商を次に使います。
図の左側では、72やその商をできるだけ小さい素数で割っていきます。例えば、最初に2で割ると、72 ÷ 2 = 36となります。次に、36をさらに2で割ると、36 ÷ 2 = 18です。このように、素数で割り続けます。
最終的に、商がすべて素数(この場合は2や3)になるまで続けていきます。結果として、72 = 2 × 2 × 2 × 3 × 3 という形になります。
3. 素因数分解の例題
3.1. 例題 1:
48
48 の素因数分解は次の通りです。
\[ 48 = 2^4 \times 3 \]
ほかにも、思いつく約数で計算すると、
\[\begin{align*} 48 &= 4\times 12 \\ &= 4^2 \times 3 \\ &= 2^4 \times 3 \end{align*}\]
3.2. 例題 2:
144
144 の素因数分解は次の通りです。
\[ 144 = 2^4 \times 3^2 \]
ほかにも、思いつく約数で計算すると、
\[\begin{align*} 144 &= 12\times 12 \\ &= 4^2 \times 3^2 \\ &= 2^4 \times 3^2 \end{align*}\]