命題の裏・逆・対偶の真偽、具体例、例題について

1. 命題
命題とは、真偽が明確に定まる文のことです。例えば、「すべての偶数は2の倍数である」は真の命題ですが、「2は奇数である」は偽の命題です。
$$p \Rightarrow q$$
pを仮定、qを結論と呼ぶ。
1.1. 命題の逆
命題「 \( p \) ならば \( q \) 」の逆とは、「 \( q \) ならば \( p \) 」です。
- 元の命題: 「雨が降れば、道路は濡れる」
- 裏: 「道路が濡れれば、雨が降った」
ここで、逆の命題は必ずしも真ではありません。例えば、「道路が濡れれば、雨が降った」という命題を考えると、道路が濡れている本当の理由は、例えばスプリンクラーが原因かもしれません。
$$q \Rightarrow p$$
1.2. 命題の裏
命題「\( p \) ならば \( q \) 」の裏は、「\( p \) でないならば \( q \) ではない」です。
- 元の命題: 「もし雨が降れば、道路は濡れる。」
- 否定: 「雨が降らないらば、道路は濡れない。」
$$\overline{p} \Rightarrow \overline{q}$$
1.3. 命題の対偶
命題「もし \( p \) ならば \( q \) 」の対偶は、「もし \( q \) でないならば \( p \) でない」です。対偶は元の命題と真偽が一致することが特徴です。
- 元の命題: 「もし雨が降れば、道路は濡れる」
- 対偶: 「もし道路が濡れていないならば、雨は降っていない」
元の命題が真であれば、対偶も真となります。また、元の命題が偽であれば、対偶も偽です。
$$\overline{q} \Rightarrow \overline{p}$$
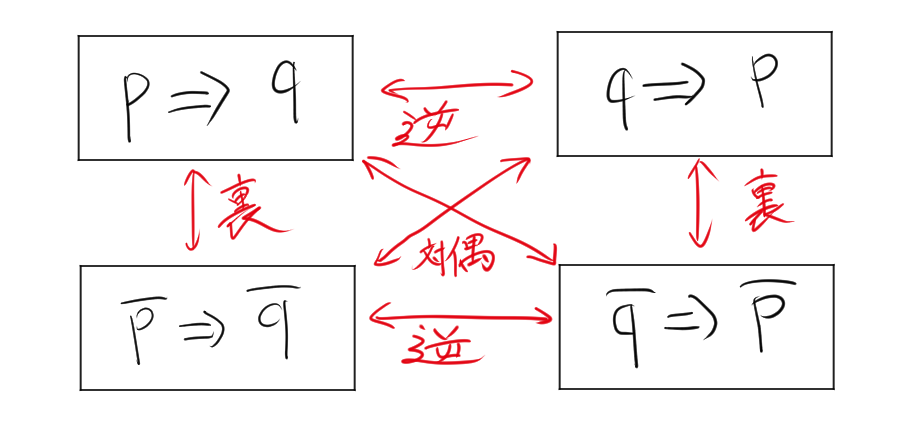
2. 対応関係
命題「pならばq」の裏・逆・対偶の関係図は次のように表すことができる。
3. 例題
3.1. 例題 1
- \( p \): 雨が降る
- \( q \): 地面が濡れる
この命題に対して、次の3つの命題を求めてください。
- 裏 (\(\overline{p} \Rightarrow \overline{q}\))
- 逆 (\(q \Rightarrow p\))
- 対偶 (\(\overline{q} \Rightarrow \overline{p}\))
- 裏の命題: 「雨が降らなければ、地面は濡れない。」
- 逆の命題: 「地面が濡れれば、雨が降っている。」
- 対偶の命題: 「地面が濡れていなければ、雨が降っていない。」
3.2. 例題 2
- \( p \): \( x \) が偶数である
- \( q \): \( x^2 \) は偶数である
この命題に対して、次の3つの命題とそれぞれの命題の真偽を求めてください。
- 裏 (\(\overline{p} \Rightarrow \overline{q}\))
- 逆 (\(q \Rightarrow p\))
- 対偶 (\(\overline{q} \Rightarrow \overline{p}\))
命題:「\( x \) が偶数ならば、\( x^2 \) は偶数である」
真です。なぜなら、偶数 \( x \) を二倍数 \( x = 2k \) とすると、\( x^2 = (2k)^2 = 4k^2 \) も偶数になります。よって、この命題は常に成立します。
裏の命題: 「\( x \) が偶数でなければ、\( x^2 \) は偶数でない。」
これは真です。もし \( x \) が奇数ならば、\( x = 2k + 1 \) となり、\( x^2 = (2k + 1)^2 = 4k^2 + 4k + 1 \) は奇数になります。したがって、\( x \) が偶数でなければ \( x^2 \) も偶数でないことがわかります。
逆の命題: 「\( x^2 \) が偶数ならば、\( x \) は偶数である。」
裏の対偶は逆であるため、裏の命題と逆の命題の真偽は一致する。したがって、真。
対偶の命題: 「\( x^2 \) が偶数でなければ、\( x \) は偶数ではない。」
命題の対偶と命題の真偽は一致する。したがって、真。
3.3. 例題 3
- \( p \): \( n \) が素数である
- \( q \): \( n \) が奇数である
この命題に対して、次の3つの命題とそれぞれの命題の真偽を求めてください。
- 裏 (\(\overline{p} \Rightarrow \overline{q}\))
- 逆 (\(q \Rightarrow p\))
- 対偶 (\(\overline{q} \Rightarrow \overline{p}\))
命題:「\( n \) が素数であれば、\( n \) は奇数である」
偽。2は素数であり、偶数であるため、この命題は偽です。
裏の命題: 「\( n \) が素数でなければ、\( n \) は奇数でない。」
偽。例えば、9や21は素数ではないですが、奇数であるため、この命題は偽です。
逆の命題: 「\( n \) が奇数であれば、\( n \) は素数である。」
偽。例えば、9や15は奇数ですが、素数ではないため、この命題は偽です。
対偶の命題: 「\( n \) が奇数でなければ、\( n \) は素数ではない。」
偽。2は偶数であり、素数であるため、この命題は偽です。