二次関数とは?最小値と最大値、グラフについて

ふゅか
二次関数って何か簡単に教えてもらえる?
はるか
二次の多項式で表される関数。
1. 二次関数
二次関数とは、二次の多項式によって表される関数のことです。一般的には、次の形で表されます。
\[ f(x) = ax^2 + bx + c \]
ここで、\(a\), \(b\), \(c\) は定数で、特に \(a \neq 0\) であることが重要です。
仮に\(a = 0\) の場合は、二次関数ではなく一次関数になってしまいます。
1.1. 二次関数のグラフ
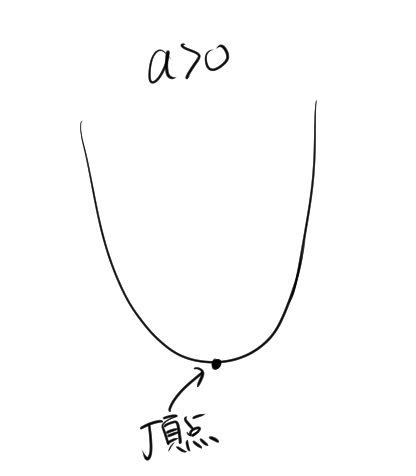
二次関数のグラフは 放物線 となります。二次関数の向きは、定数 \(a\) の値によって決まります。
- \(a > 0\) の場合、放物線は下に凸(上に開く)。
- \(a < 0\) の場合、放物線は上に凸(下に開く)。
ふゅか
二次関数のグラフって、どんな形になるの?
はるか
放物線。
1.2. 具体的なグラフ
具体的に、二次関数はどんなグラフになるのか見ていきましょう。
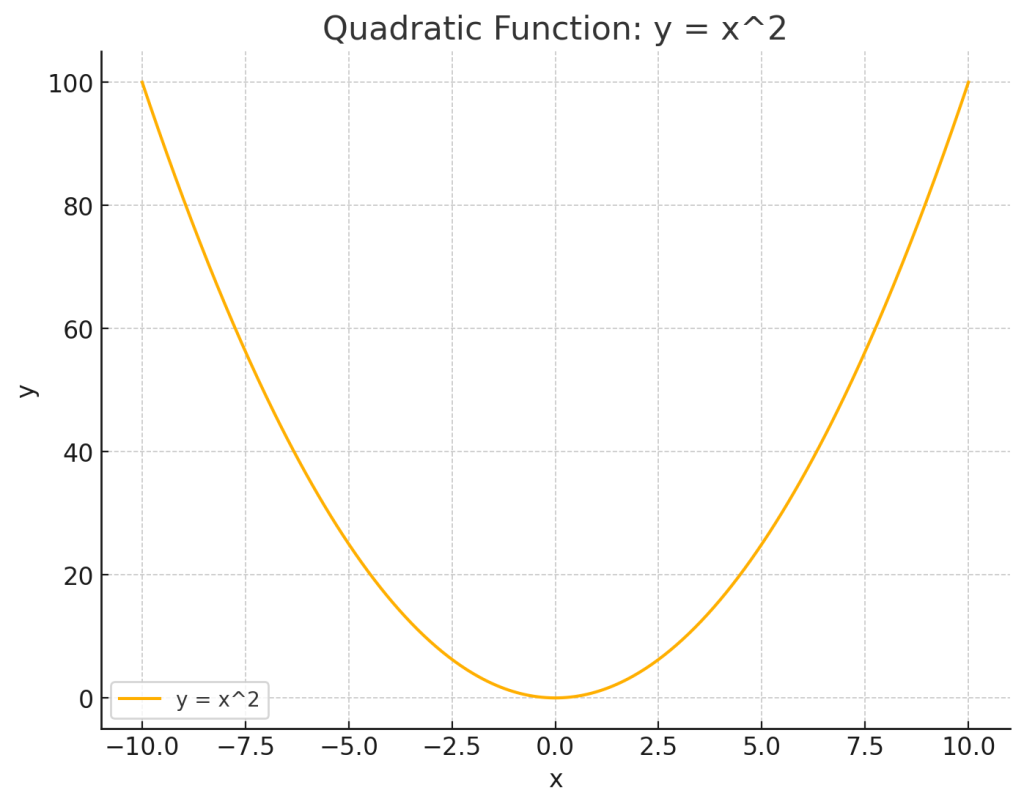
\( y = x^2 \)
この関数は最も基本的な二次関数です。グラフは頂点が原点 \( (0, 0) \) にある放物線で、下に凸です。
頂点は最小値であり、\( y = 0 \) です。
ふゅか
基本的な二次関数、\( y = x^2 \) のグラフはどうなるの?
はるか
原点 \( (0, 0) \) を頂点に持つ、下に凸な放物線。
ふゅか
ふむふむ、頂点が最小値で、\( y = 0 \) になるんだね!じゃあ、次は \( y = x^2 + 3x \) を見てみよう♪
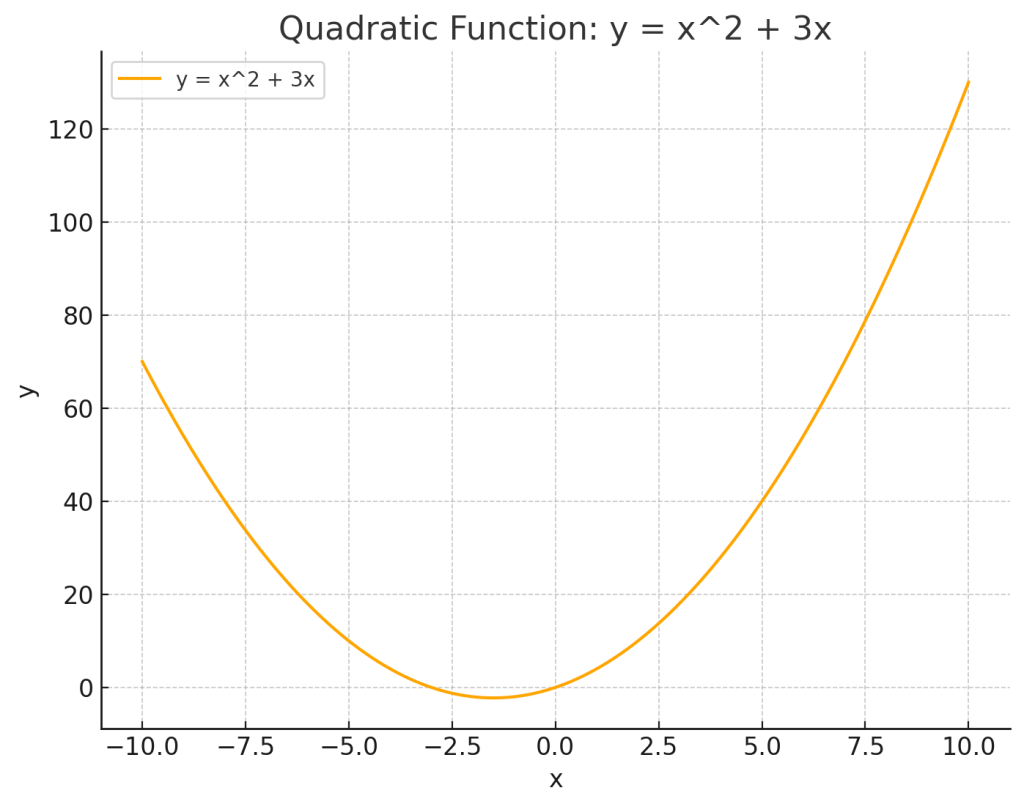
\( y = x^2 + 3x \)
この関数は \( x^2 \) に \( 3x \) が加わったもので、放物線の形は$x^2$と変わらないものの、原点から少しずれています。
頂点は \( (-\frac{3}{2}, -\frac{9}{4}) \) に位置しており、原点より低い位置にあります。
はるか
このグラフは少しずれて、頂点が \( (-\frac{3}{2}, -\frac{9}{4}) \)。
ふゅか
なるほど〜。原点からずれてるけど、基本の形は変わらないんだね!最後に \( y = -x^2 + 2x \) を見てみよう!
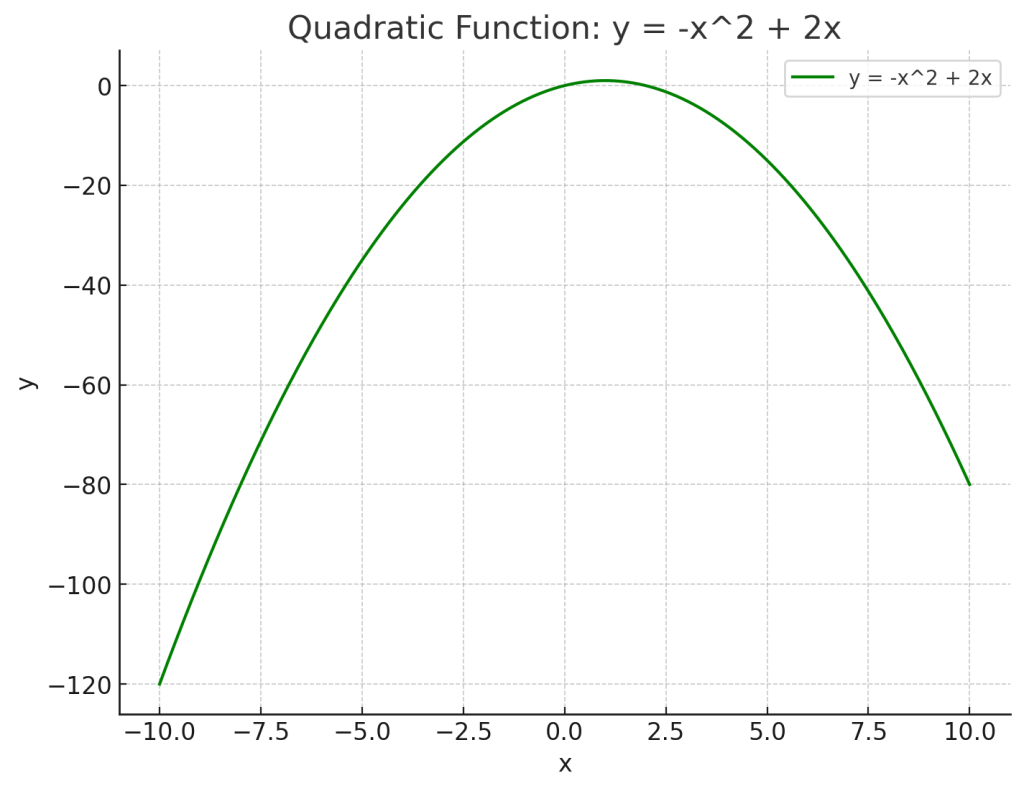
\( y = -x^2 + 2x \)
この関数は \( x^2 \) にマイナス符号がついたもので、上の2つのグラフとは異なり、二次関数が上に凸になっています。
頂点は \( (1, 1) \) にあり、この点がグラフの最高点(最大値)となり、原点より高い位置にあります。
ふゅか
このグラフは上に凸になってる!
はるか
そう。頂点は \( (1, 1) \) で、この点が最大値。
ふゅか
へぇ〜、上に凸だと最大値が存在するんだね。
2. 最大値と最小値
二次関数の最大値と最小値については、放物線の 頂点 を基に考えることができます。
2.1. 最小値(\(a > 0\) の場合)
下に凸になる放物線(\(a > 0\))では、放物線の頂点が 最小値 となります。
このとき、二次関数は 全体で最小値を持ちます が、最大値は存在しません。
2.2. 最大値(\(a < 0\) の場合)
上に凸になる放物線(\(a < 0\))では、頂点が 最大値 となります。
この場合、最大値は存在しますが、最小値は存在しません。
2.3. まとめ
- \(a > 0\) の場合:最小値が存在し、最大値はなし。
- \(a < 0\) の場合:最大値が存在し、最小値はなし。
PR