【最大値と最小値の例題】二次関数の頂点の求め方と成り立つ理由、例題について!

1. 二次関数の頂点
\[ \left( -\frac{b}{2a}, -\frac{b^2}{4a} + c \right) \]
このとき、$x=-\frac{b}{2a}$を軸と呼ぶ。(頂点のx座標)
二次関数の頂点を求めるとき、平方完成を利用します。
1.1. 平方完成
平方完成を利用して、実際に頂点を求めてみます。まず \(a\) で括ります。
\[ y = a \left( x^2 + \frac{b}{a}x \right) + c \]
平方完成するために、\( \frac{b^2}{4a^2} \) の二乗を加えることで、平方の形を作ります。
\[ \begin{align*}y &=a \left( x^2 + \frac{b}{a}x +\frac{b^2}{4a^2}- \frac{b^2}{4a^2}\right) + c \\ &=a \left( \left( x + \frac{b}{2a} \right)^2 – \frac{b^2}{4a^2} \right) + c \end{align*}\]
この時、\(\frac{b^2}{4a^2}\) を引くことで、元の式に影響がないようにしています。次に、定数部分をまとめます。
\[ y = a \left( x + \frac{b}{2a} \right)^2 – \frac{b^2}{4a} + c \]
1.2. 頂点の座標
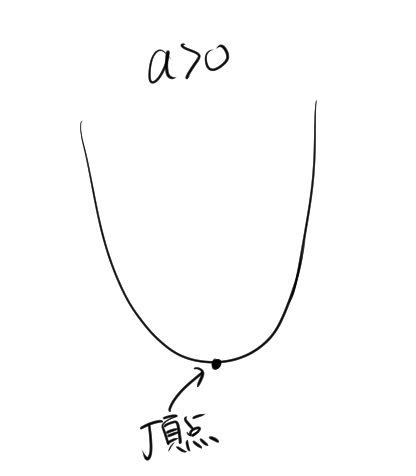
1.2.1. a>0の場合
平方完成後の式を見ると、\( a\left( x + \frac{b}{2a} \right)^2 \) の形になっています。$a>0$より、\( a\left( x + \frac{b}{2a} \right)^2 \) は0以上であるから、次の不等式が成り立つ。
$$a \left( x + \frac{b}{2a} \right)^2 – \frac{b^2}{4a} + c \geqq 0 – \frac{b^2}{4a} +c$$
不等式より、二次関数の$x$がどのような値をとろうとも、$- \frac{b^2}{4a} +c$以上の値になることがわかる。また、不等式の等号が成立するのは \( x = -\frac{b}{2a} \) のときです。したがって、この \(x\) の値が頂点の \(x\) 座標になります。また、対応する \(y\) の値は
\[ y = -\frac{b^2}{4a} + c \]
ですので、頂点の座標は
\[ \left( -\frac{b}{2a}, -\frac{b^2}{4a} + c \right) \]
となります。
1.2.2. a<0の場合
$a<0$より、\( a\left( x + \frac{b}{2a} \right)^2 \) は0以下であるから、次の不等式が成り立つ。
$$a \left( x + \frac{b}{2a} \right)^2 – \frac{b^2}{4a} + c \leqq 0 – \frac{b^2}{4a} +c$$
不等式より、二次関数の$x$がどのような値をとろうとも、$- \frac{b^2}{4a} +c$以下の値になることがわかる。
また、不等式の等号が成立するのは \( x = -\frac{b}{2a} \) のときです。したがって、この \(x\) の値が頂点の \(x\) 座標になります。また、対応する \(y\) の値は
\[ y = -\frac{b^2}{4a} + c \]
ですので、頂点の座標は
\[ \left( -\frac{b}{2a}, -\frac{b^2}{4a} + c \right) \]
となります。
2. 例題
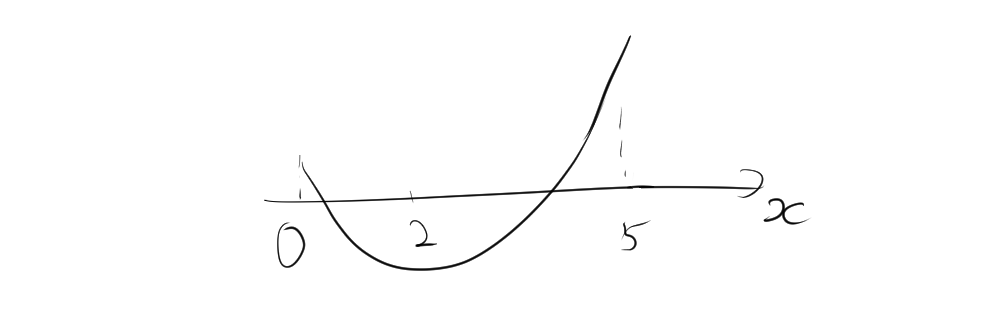
2.1. 問題 1: 軸が定義域内にある場合
平方完成を行います。 \[ f(x) = x^2 – 4x + 1 = (x – 2)^2 – 3 \] これにより、頂点は \( (2, -3) \) であることが分かります。
定義域$0 \leqq x \leqq 5$ における端点での関数値を求めます。
\( f(0) = 0^2 – 4(0) + 1 = 1 \)
\( f(5) = 5^2 – 4(5) + 1 = 6 \)
頂点 \( (2, -3) \) が定義域内にあるため、この点でも関数値を確認します。
\( f(2) = (2 – 2)^2 – 3 = -3 \)
よって、定義域$0 \leqq x \leqq 5$における最大値は 6、最小値は -3 です。
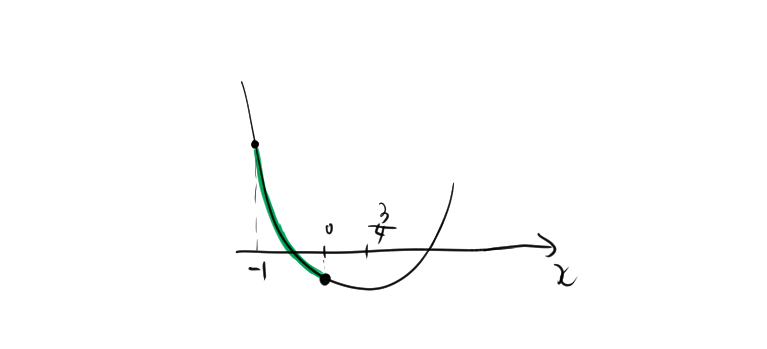
2.2. 問題 2: 軸が定義域より右にある場合
平方完成を行います。
\[ f(x) = -2x^2 + 3x + 1 = -2\left(x – \frac{3}{4} \right)^2 + \frac{25}{8} \]
これにより、軸は \( x = \frac{3}{4} \) にあります。軸 \( x = \frac{3}{4} \) は定義域 $-1 \leqq x \leqq 0$の外側にありますので、定義域の端点での関数値を求めます。
\( f(-1) = -2(-1)^2 + 3(-1) + 1 = -4 \)
\( f(0) = -2(0)^2 + 3(0) + 1 = 1 \)
よって、定義域 $-1 \leqq x \leqq 0$ における最大値は 1、最小値は -4 です。
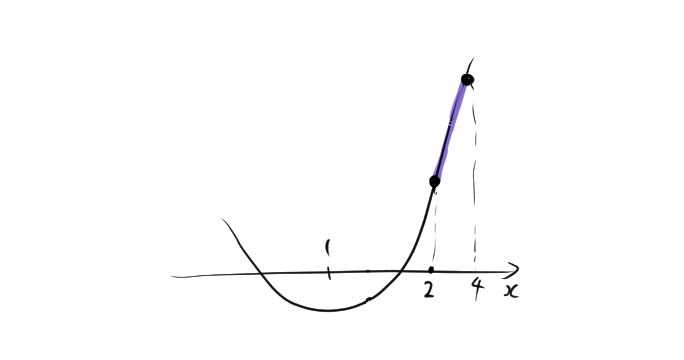
2.3. 問題 3: 軸が定義域より左にある場合
平方完成を行います。 \[ f(x) = 3(x – 1)^2 – 1 \] これにより、軸は \( x = 1 \) にあります。
軸 \( x = 1 \) は定義域 $2 \leqq x \leqq 4$ の外側にあるため、定義域の端点での関数値を求めます。
\( f(2) = 3(2)^2 – 6(2) + 2 = 2 \)
\( f(4) = 3(4)^2 – 6(4) + 2 = 26 \)
よって、定義域 $2 \leqq x \leqq 4$ における最大値は 26、最小値は -2 です。