ラジアンの意味と単位について

はるか

ラジアンって聞いたことある？

ふゅか

うん！角度を表す単位で、度数法とはちょっと違うんだよね。

はるか

円の半径と同じ長さの弧が作る角度。それが1ラジアン。

1. ラジアンとは？

ラジアンは、角度を表す単位の一つで、主に数学や物理の分野で使用されます。一般的に使われる度数法（°）に対して、ラジアンは円の特性に基づいた単位です。

1.1. ラジアンの単位

• 弧の長さ: 円周の一部を指します。
• 半径: 円の中心から外周までの距離です。

例えば、円の中心角が 1 ラジアンのとき、その角に対応する弧の長さは円の半径と等しくなります。

また、半径が1、弧の長さが$2\pi$(円周)であるときは、$2\pi$ラジアンになる。

はるか

弧の長さが半径と同じなら、その角度が1ラジアンになる。

ふゅか

なるほど！例えば、半径2の円なら、弧の長さが2のときの角度が1ラジアンになるってこと？

はるか

そう。それがラジアンの基本的な考え方。

1.2. ラジアンの直感的なイメージ

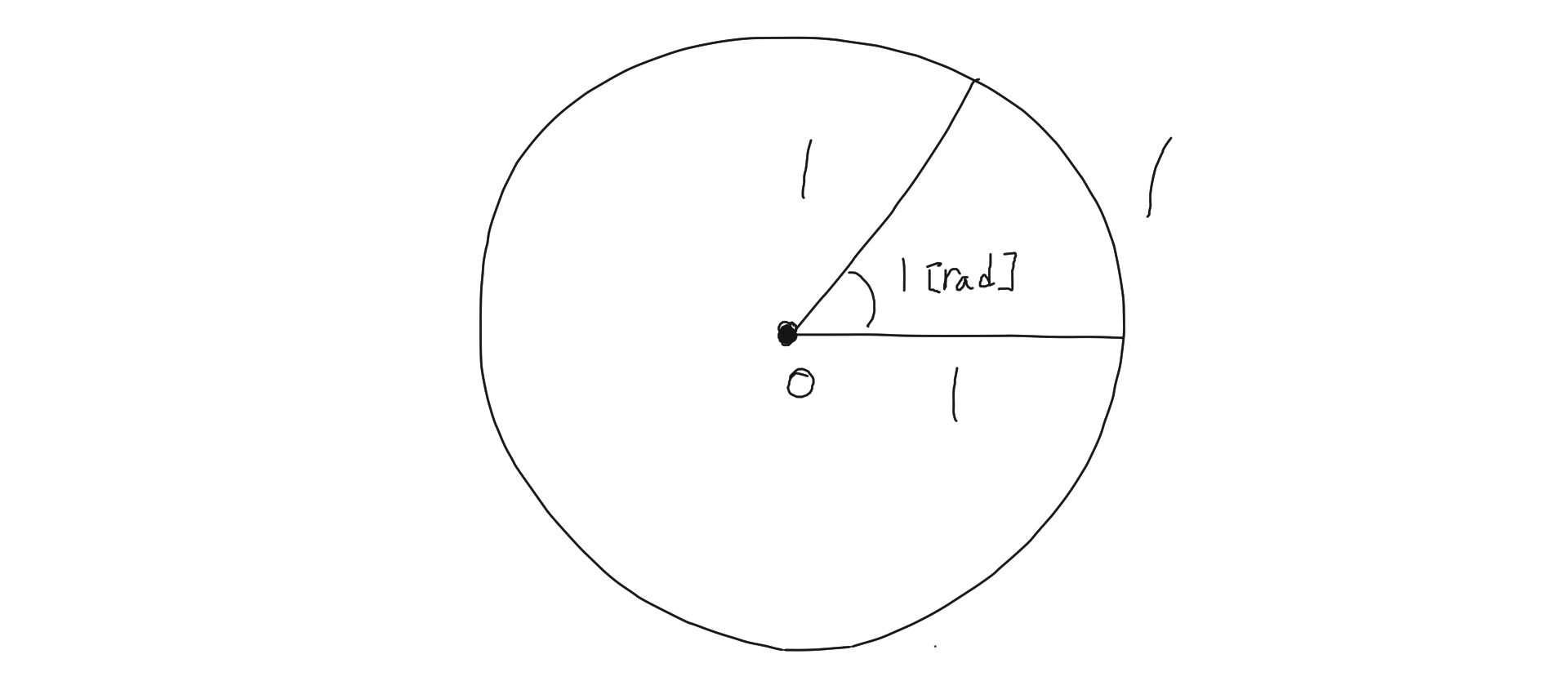
ラジアンをイメージするために、以下の図を考えてみてください：

1. 円を描き、半径を1とします。
2. 円周の一部を切り取り、その長さも1とします。
3. その弧の両端を結ぶとできる角が、ちょうど 1ラジアン です。

2. 度数法との関係

ラジアンは度数法と相互に変換できます。一回転は\(360°\) で、\(2\pi\)ラジアンに対応するので、

\[ 1 \text{ラジアン} = \frac{180°}{\pi} \] \[ 1° = \frac{\pi}{180} \text{ラジアン} \]

例えば：

• \(90° = \frac{\pi}{2}\) ラジアン
• \(180° = \pi\) ラジアン

3. ラジアンと三角関数の関係

1. \(0\) ラジアン：点は \((1, 0)\) に位置し、\(\cos(0) = 1\)、\(\sin(0) = 0\)
2. \(\frac{\pi}{2}\) ラジアン：点は \((0, 1)\) に位置し、\(\cos\left(\frac{\pi}{2}\right) = 0\)、\(\sin\left(\frac{\pi}{2}\right) = 1\)
3. \(\pi\) ラジアン：点は \((-1, 0)\) に位置し、\(\cos(\pi) = -1\)、\(\sin(\pi) = 0\)