正規文法と定義・具体例・生成規則・例題・有限オートマトンについて

1. 正規文法とは
$$G = \langle N, \Sigma, P, S \rangle$$
- \( N \):非終端記号の集合。
- これは文法の生成規則で使われる記号の集合です。通常、大文字のアルファベット(例:\( A, B, C \))が使われます。
- \( \Sigma \):終端記号の集合。
- これは文法が生成する最終的な文字列に含まれる記号の集合で、通常小文字のアルファベット(例:\( a, b, c \))が使われます。終端記号は文法によって生成される言語の「単語」に対応します。
- \( P \):生成規則の集合。
- これは文法のルールの集合で、記号がどのように置き換えられるかを定義します。正規文法の場合、生成規則は次のいずれかの形をとります。
- 右正規文法: \( A \rightarrow aB \) または \( A \rightarrow a \)
- 左正規文法: \( A \rightarrow Ba \) または \( A \rightarrow a \)
- ここで、\( A, B \in N \) であり、\( a \in \Sigma \) です。
- これは文法のルールの集合で、記号がどのように置き換えられるかを定義します。正規文法の場合、生成規則は次のいずれかの形をとります。
- \( S \):開始記号。
- \( N \) の中の特定の記号で、文法の生成を開始するための出発点です。
1.1. 正規文法の例
例えば、以下の右正規文法 \( G = \langle N, \Sigma, P, S \rangle \) を考えます。
- \( N = \{ S, A \} \)
- \( \Sigma = \{ a, b \} \)
- \( P = \{ S \rightarrow aA, A \rightarrow b, A \rightarrow bS\} \)
- \( S = S \)
この文法は、「a」で始まり、「b」で終わる文字列を生成します。例えば、「ab」や「abbbbbbb」などの文字列が生成されます。
2. 正則文法とオートマトン
2.1. オートマトンと形式文法の対応関係
| 形式文法 | オートマン |
|---|---|
| 句構造文法 | チューリングマシン |
| 文脈依存文法 | 線形有界オートマトン |
| 文脈自由文法 | プッシュダウンオートマトン |
| 正則文法(正規文法) | 有限オートマトン |
2.2. 正規文法から有限オートマトン
- 正規文法 \( G = (N, Σ, P, S) \):
- \( N \) は非終端記号の有限集合。
- \( Σ \) は終端記号の有限集合。
- \( P \) は生成規則の有限集合で、以下の形式を持つ:
- \( A \to aB \) (ここで \( A, B \in N \), \( a \in Σ \))
- \( A \to a \) (ここで \( A \in N \), \( a \in Σ \))
- \( S \in N \) は開始記号。
次のようにして、オートマトン \( M \) を構成します。
- 状態集合 \( Q \)
- \( Q = N \cup \{q\} \)
- ここで \( q \) は \( N \) に含まれない状態です。受理状態のために作成。
- 入力アルファベット \( Σ \)
- \( Σ \) は文法 \( G \) の終端記号の集合と同じです。
- 遷移関数 \( δ \)
- \( δ: Q \times Σ \to 2^Q \) を次のように定義します。
- 各生成規則 \( A \to aB \) (\( A, B \in N \), \( a \in Σ \))に対して、\( δ(A, a) = B \) とします。
- 各生成規則 \( A \to a \) (\( A \in N \), \( a \in Σ \))に対して、\( δ(A, a) = q \) とします。
- 開始状態 \( S \)
- 開始状態 \( S \) は文法 \( G \) の開始記号と同じです。
- 受理状態 \( F \)
- \( F = \{q\} \) です。ただし、開始記号の生成規則に空文字を含む場合は、初期状態も含みます。(\( F = \{q\}\cup \{S\} \) )
2.3. 有限オートマトンから正規文法
まず、DFA \( M = (Q, Σ, δ, q_0, F) \) を次のように定義します。
- \( Q \) は状態の有限集合。
- \( Σ \) は入力アルファベットの有限集合。
- \( δ \) は遷移関数で、\( δ: Q \times Σ \to Q \) です。
- \( q_0 \in Q \) は開始状態。
- \( F \subseteq Q \) は受理状態の集合です。
この DFA \( M \) が受理する言語 \( L(M) \) を生成する正規文法 \( G = \langle N, Σ, P, S \rangle \) を次のように構成します。
- 非終端記号の集合 \( N \)
- \( N \) を \( M \) の状態集合 \( Q \) と同じ集合に設定します。つまり、\( N = Q \) とします。
- これにより、文法 \( G \) の非終端記号はすべての状態に対応することになります。
- 終端記号の集合 \( Σ \)
- \( Σ \) は DFA \( M \) の入力アルファベットと同じ集合です。したがって、文法 \( G \) の終端記号の集合も \( M \) の入力アルファベット \( Σ \) となります。
- 開始記号 \( S \)
- 文法 \( G \) の開始記号 \( S \) は、DFA \( M \) の開始状態 \( q_0 \) に対応させます。つまり、\( S = q_0 \) とします。
- 生成規則の集合 \( P \)
- 各遷移 \( δ(A, a) = B \) に対して、生成規則 \( A \to aB \) を \( P \) に含めます。これは、状態 \( A \) から入力 \( a \) を経て状態 \( B \) へ遷移することに対応します。
- さらに、もし状態 \( B \) が受理状態 \( F \) に含まれる場合、生成規則 \( A \to a \) を \( P \) に追加します。これにより、状態 \( A \) から受理状態に至る過程で終端記号列を生成することができます。
- また、DFA の開始状態 \( q_0 \) が受理状態 \( F \) に含まれる場合は、空文字列 \( \epsilon \) を生成するための生成規則 \( S \to \epsilon \) を \( P \) に含めます。
このようにして構成された正規文法 \( G = \langle N, Σ, P, S \rangle \) が、DFA \( M \) の受理する言語 \( L(M) \) を生成することができます。
3. 正規文法とオートマトンに関連する例題
3.1. 正規文法からオートマトンを作成する例題
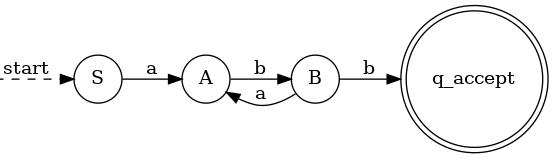
- 非終端記号集合 N: {S, A, B}
- 終端記号集合 Σ: {a, b}
- 開始記号 S: S
- 生成規則 P:
- S → aA
- A → bB
- B → aA | b
NFAは次のように作成することができます。
3.2. オートマトンから正規文法を作成する例題
| 状態 | 入力 | 遷移先状態 |
|---|---|---|
| q0 | a | q1 |
| q0 | b | q2 |
| q1 | a | q1 |
| q1 | b | q3 |
| q2 | a | q3 |
| q2 | b | q2 |
| q3 | a | q0 |
| q3 | b | q1 |
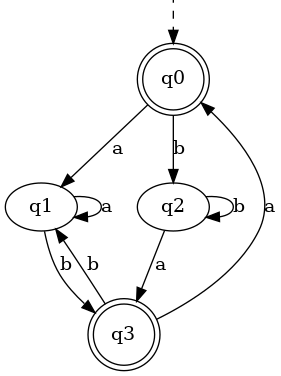
このオートマトンの開始状態は \( q0 \)、受理状態は \( q3 \) とします。
以下の状態遷移表に基づいて、オートマトンから正規文法を作成します。
- 開始状態: \( q0 \)
- 受理状態: \( q3 \)
状態遷移表に基づいて、次のように正規文法を作成できます。
- \( q0 \) の遷移
- \( q0 \) に \( a \) を入力すると \( q1 \) に遷移する: \[ S \rightarrow aA \]
- \( q0 \) に \( b \) を入力すると \( q2 \) に遷移する: \[ S \rightarrow bB \]
- \( q1 \) の遷移
- \( q1 \) に \( a \) を入力すると \( q1 \) に遷移する: \[ A \rightarrow aA \]
- \( q1 \) に \( b \) を入力すると \( q3 \) に遷移する: \[ A \rightarrow bC \]
- \( q2 \) の遷移
- \( q2 \) に \( a \) を入力すると \( q3 \) に遷移する: \[ B \rightarrow aC \]
- \( q2 \) に \( b \) を入力すると \( q2 \) に遷移する: \[ B \rightarrow bB \]
- \( q3 \) の遷移(受理状態なので、ここで終了する規則も含めます)
- \( q3 \) に \( a \) を入力すると \( q0 \) に遷移する: \[ C \rightarrow aS \]
- \( q3 \) に \( b \) を入力すると \( q1 \) に遷移する: \[ C \rightarrow bA \]
- \( q3 \) は受理状態なので、空文字列を生成する規則も含める: \[ C \rightarrow \epsilon \]
オートマトンに対応する正規文法は以下の通りです。
\[ \begin{aligned} S &\rightarrow aA \ | \ bB \\ A &\rightarrow aA \ | \ bC \\ B &\rightarrow aC \ | \ bB \\ C &\rightarrow aS \ | \ bA \ | \ \epsilon \end{aligned} \]
これで、オートマトンから正規文法を作成できました。
また、状態遷移表からオートマトンを作成すると次のようになります。