ロルの定理の証明、イメージと具体例について

はるか

ロルの定理って、関数が区間の端で同じ値を持つとき、途中で一度は平らになるっていうやつね。

ふゅか

そうそう！それが直感的なイメージね。例えば山の両端が同じ高さなら、どこかで水平になる地点があるって感じだね！

1. ロルの定理とは

1.1. ロルの定理

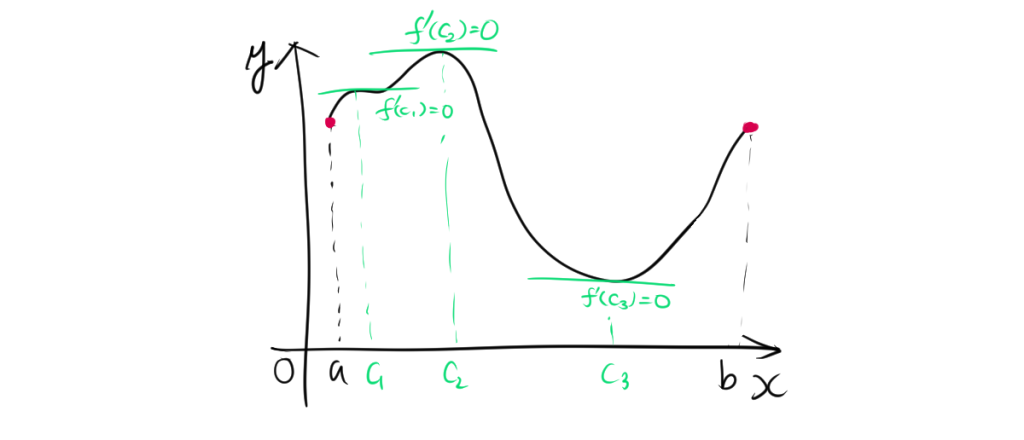
1.2. 直感的なイメージ

ロルの定理は、グラフの形状に基づいて直感的に理解することができます。関数 \( f \) のグラフが \([a, b]\) の両端で同じ高さ（つまり \( f(a) = f(b) \)）であり、途中のどこかで増加または減少している場合、グラフは最低でも一度は水平になる必要があります。この「水平になる」点は、接線の傾きがゼロ、すなわち導関数がゼロになる点を意味します。

1.3. ロルの定理の例

例えば、関数 \( f(x) = (x-1)(x-2)(x-3) \) を考えます。この関数は多項式であり、実数全体で連続かつ微分可能です。また、\( x = 1 \) と \( x = 3 \) では \( f(1) = f(3) = 0 \) となります。ロルの定理を適用すると、少なくとも1つの \( c \) (\(1 < c < 3\)) が存在し、その点で \(x-1)0 = 0 \) となります。

実際に微分してみると、 \[ f'(x) = 3x^2 – 12x + 11 \] となります。この式の根を求めると、2つの実数解 \( x = \frac{6 \pm \sqrt{3}}{3} \) があり、これらは \( x = 1 \) と \( x = 3 \) の間に位置します。このため、ロルの定理が正しいことが確認できます。

2. ロルの定理の証明

ふゅか

証明のところも面白いよね。最大値を持つ場合と最小値を持つ場合で考えるけど、どちらの場合でも接線の傾きがゼロになる点があることを示すの。

はるか

最大値か最小値を持つなら、その場所で接線が水平になる、つまり傾きがゼロだと考える。

2.1. 最大値を持つ場合

関数 \( f \) は閉区間 \([a, b]\) で連続なので、最大値・最小値の定理により、少なくとも1つの \( c \in [a, b] \) が存在し、そこで \( f(x) \) は最大値を持ちます。この場合、最大値を持つと仮定します。すなわち、任意の$x$に対して、

\[ f(c) \geq f(x) \]

$c$から$\Delta x$だけずらして関数fについて考える。

関数 \( f \) は \( c \) で最大値を持つので、

\[ f(c + \Delta x) \leq f(c) \]

両辺に \( f(c) \) を引くと、 \[ f(c + \Delta x) – f(c) \leq 0 \]

\(\Delta x > 0\) のとき、

不等式を \(\Delta x\) で割ると、

\[ \frac{f(c + \Delta x) – f(c)}{\Delta x} \leq 0 \]

\(\Delta x \to 0\) とすると、

\[ \lim_{\Delta x \to 0} \frac{f(c + \Delta x) – f(c)}{\Delta x} = f'(c) \leq 0 \]

\(\Delta x < 0\) のとき、

不等式を \(\Delta x\) で割ると、

\[ \frac{f(c + \Delta x) – f(c)}{\Delta x} \geq 0 \]

\(\Delta x \to 0\) とすると、 \[ \lim_{\Delta x \to 0} \frac{f(c + \Delta x) – f(c)}{\Delta x} = f'(c) \geq 0 \]

したがって、\( f'(c) \) は \( 0 \leq f'(c) \leq 0 \) となり、 \[ f'(c) = 0 \]

2.2. 最小値を持つ場合

関数 \( f \) は同様に閉区間 \([a, b]\) で連続なので、最大値・最小値の定理より、\( c \in [a, b] \) で最小値を持つと仮定します。すなわち、任意の$x$に対して、

\[ f(c) \leq f(x)\]

$c$から$\Delta x$だけずらして関数fについて考える。

関数 \( f \) は \( c \) で最小値を持つので、 \[ f(c + \Delta x) \geq f(c) \]

両辺に \( f(c) \) を引くと、 \[ f(c + \Delta x) – f(c) \geq 0 \]

\(\Delta x > 0\) のとき、

不等式を \(\Delta x\) で割ると、

\[ \frac{f(c + \Delta x) – f(c)}{\Delta x} \geq 0 \]

\(\Delta x \to 0\) とすると、

\[ \lim_{\Delta x \to 0} \frac{f(c + \Delta x) – f(c)}{\Delta x} = f'(c) \geq 0 \]

\(\Delta x < 0\) のとき、

不等式を \(\Delta x\) で割ると、

\[ \frac{f(c + \Delta x) – f(c)}{\Delta x} \leq 0 \]

\(\Delta x \to 0\) とすると、

\[ \lim_{\Delta x \to 0} \frac{f(c + \Delta x) – f(c)}{\Delta x} = f'(c) \leq 0 \]

したがって、\( f'(c) \) は \( 0 \leq f'(c) \leq 0 \) となり、 \[ f'(c) = 0 \]

以上より、最大値と最小値の両方の場合について、少なくとも1つの \( c \in (a, b) \) が存在し、\( f'(c) = 0 \) であることが示されました。