複素数の回転と拡大縮小の意味、具体例、計算問題について

はるか

複素数の回転と拡大について、基本的なところから始める。

ふゅか

そうね！複雑な計算をシンプルにできるんだよね！

1. 複素数の回転と拡大

1.1. 複素数の積が回転・拡大する理由

ふゅか

例えば、複素数をr倍して角度を$\alpha$だけ回転させると、新しい複素数はどうなるかな？それを一緒に見てみよう！

複素数$\alpha=r_1(\cos\theta+i\sin\theta)$としたときに、複素数$r_2(\cos\alpha+i\sin\alpha)$をかけると以下のようになる。

$r_1(\cos\theta+i\sin\theta)r_2(\cos\alpha+i\sin\alpha)$

$=r_1r_2\lbrace\cos\theta\cos\alpha-\sin\theta\sin\alpha+(i\cos\theta\sin\alpha+\sin\theta\cos\alpha)\rbrace$

加法定理を用いると、

$=r_1r_2\lbrace\cos(\theta+\alpha)+i\sin(\theta+\alpha)\rbrace$

となり、原点を中心に$\alpha$だけ回転して、原点からの距離が$r_2$倍されたことがわかる。

1.2. 具体例

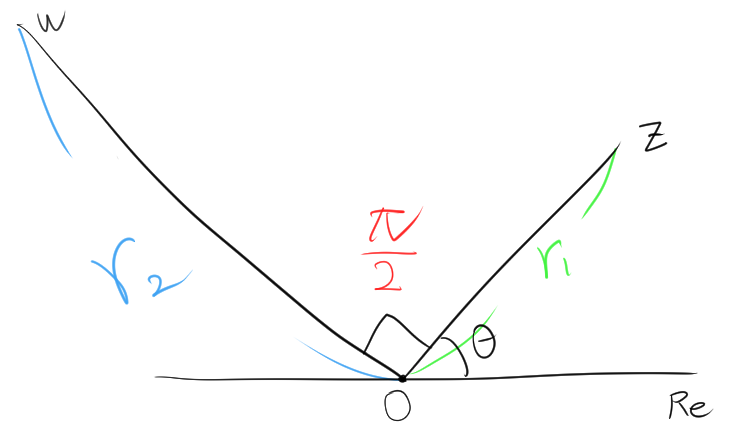
次の画像の様に、複素数zをwに回転と拡大を行ったとします。

このとき、$z$に対して、$\dfrac{r_2}{r_1}\left(\cos\dfrac{\pi}{2}+i\sin\dfrac{\pi}{2}\right)$をかければ、$w$が得られる。zは${r_1}\left(\cos\theta+i\sin\theta\right)$とあらわすことができるので、

$w=r_2\left(\cos\left(\theta+\dfrac{\pi}{2}\right)+i\sin\left(\theta+\dfrac{\pi}{2}\right)\right)$

2. 原点以外における回転

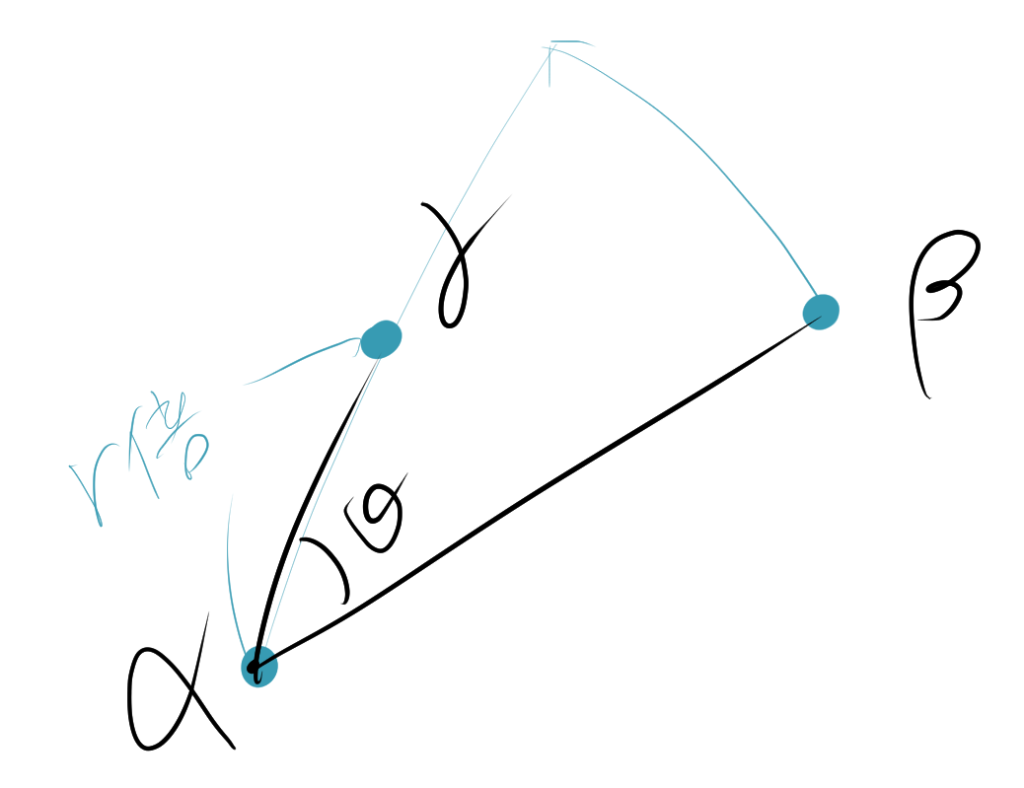
複素数平面上の図形とベクトルで解説したようなベクトル的な考えを用いて考える。

$\beta-\alpha$を$r$倍して$\theta$だけ回転した複素数が$\gamma-\alpha$となるため、

$\gamma-\alpha=(\beta-\alpha)r(\cos\theta+i\sin\theta)$

$\gamma=r(\beta-\alpha)(\cos\theta+i\sin\theta)+\alpha$

3. 例題

はるか

じゃあ、計算問題を解いてみよう。複素数$z = 1 + i$を原点を中心に回転させる

ふゅか

うん！そして、次はその結果を使って、$z$を中心に$-\dfrac{\pi}{3}$回転させたものを計算してみるわね！

(1)複素数$z$を極形式を用いて表すと、

$z=\sqrt{2}\left(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\right)$

となる。複素数$z$を$\dfrac{\pi}{4}$回転したものを複素数$w$とすると、

$w=z\left(\cos\dfrac{\pi}{4}+\sin\dfrac{\pi}{4}\right)$

$=\sqrt{2}\left(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\right)\left(\cos\dfrac{\pi}{4}+\sin\dfrac{\pi}{4}\right)$

$=\sqrt{2}\left(\cos\left(\dfrac{\pi}{4}+\dfrac{\pi}{4}\right)+\sin\left(\dfrac{\pi}{4}+\dfrac{\pi}{4}\right)\right)$

$=\sqrt{2}\left(\cos\dfrac{\pi}{2}+i\sin\dfrac{\pi}{2}\right)$

$=\sqrt{2}i$

となるから、$w_1=3w$より、

$w_1=3\sqrt{2}i$

(2)$w_2$を求めると以下のようになる。

$$w_2-z=(w_1-z)\left(\cos\left(-\dfrac{\pi}{3}\right)+i\sin\left(-\dfrac{\pi}{3}\right)\right)$$

\[ w_2 – z = (-1 + (3\sqrt{2} – 1)i) \cdot \left(\frac{1}{2} – i\frac{\sqrt{3}}{2}\right) \]

この式を展開すると、

\[ w_2 – z = (-1) \cdot \frac{1}{2} + (-1) \cdot \left(-i\frac{\sqrt{3}}{2}\right) + (3\sqrt{2} – 1)i \cdot \frac{1}{2} + (3\sqrt{2} – 1)i \cdot \left(-i\frac{\sqrt{3}}{2}\right) \]

\[ w_2 – z = \frac{-1 + 3\sqrt{6} – \sqrt{3}}{2} + \frac{\sqrt{3} + 3\sqrt{2} – 1}{2}i \]

\[ w_2 = \left(1 + \frac{-1 + 3\sqrt{6} – \sqrt{3}}{2}\right) + \left(1 + \frac{\sqrt{3} + 3\sqrt{2} – 1}{2}\right)i \]

\[ w_2 = \frac{2 – 1 + 3\sqrt{6} – \sqrt{3}}{2} + \frac{2 + \sqrt{3} + 3\sqrt{2} – 1}{2}i \]

\[ w_2 = \frac{1 + 3\sqrt{6} – \sqrt{3}}{2} + \frac{1 + \sqrt{3} + 3\sqrt{2}}{2}i \]