スカラー3重積の定義・性質・例題・平行六面体について

1. スカラー3重積

ここで、$\mathbf{b} \times \mathbf{c}$ はベクトル $\mathbf{b}$ と $\mathbf{c}$ の外積であり、その結果得られるベクトルは $\mathbf{b}$ と $\mathbf{c}$ 両方に垂直なベクトルです。次に、このベクトルと $\mathbf{a}$ の内積をとりす。

1.1. スカラー3重積の成分の計算

スカラー三重積 $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$ を成分を用いて計算する方法を説明します。まず、ベクトル $\mathbf{a}$, $\mathbf{b}$, $\mathbf{c}$ の成分を以下のように設定します。

$$\mathbf{a} = (a_1, a_2, a_3), \quad \mathbf{b} = (b_1, b_2, b_3), \quad \mathbf{c} = (c_1, c_2, c_3)$$

1.1.1. ステップ 1: 外積 $\mathbf{b} \times \mathbf{c}$ の計算

ベクトルの外積は、次のように計算されます。

$$\mathbf{b} \times \mathbf{c} = \left( b_2 c_3 – b_3 c_2, b_3 c_1 – b_1 c_3, b_1 c_2 – b_2 c_1 \right)$$

1.1.2. ステップ 2: 内積 $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$ の計算

外積の結果を用いて内積を計算します。

$$\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = a_1 (b_2 c_3 – b_3 c_2) + a_2 (b_3 c_1 – b_1 c_3) + a_3 (b_1 c_2 – b_2 c_1)$$

1.2. スカラー3重積の計算問題

まず、$\mathbf{b}$と $\mathbf{c}$の外積を計算すると、

$\mathbf{b} \times \mathbf{c}$

$= \begin{bmatrix} 2\times 0 – 4\times 5 \\ -1 \times 4 – 1 \times 2 \\ 1\times 5 -0 \times (-1) \\ \end{bmatrix}$

$= \begin{bmatrix} -20 \\ -6 \\ 5 \\ \end{bmatrix}$

次に内積を計算する。

$\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})= \begin{bmatrix} 2 \\ 3 \\ -1 \\ \end{bmatrix} \cdot \begin{bmatrix} -20 \\ -6 \\ 5 \\ \end{bmatrix}$

$= -63$

2. 行列式を用いる方法

この行列式は、ベクトル $\mathbf{a}$, $\mathbf{b}$, $\mathbf{c}$ の各成分からなる $3 \times 3$ 行列の行列式です。

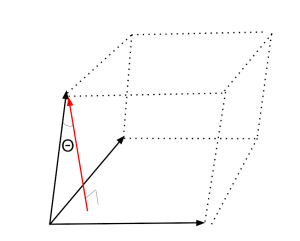
3. 平行六面体

3.1. 平行六面体になる証明

図のように$0<\theta\leq \dfrac{\pi}{2}$とする。底面の面積をAとすると、

$$A=|\mathbf{b} \times \mathbf{c}|$$

とあらわすことができる。そして、高さを$h$とすると、

$$h=|\mathbf{a}|\cos\theta$$

とあらわすことができる。

したがって、体積$V$は

$$V=Ah$$

$$=|\mathbf{b} \times \mathbf{c}||\mathbf{a}|\cos\theta$$

$$=\mathbf{a}\cdot (\mathbf{b} \times \mathbf{c})$$

となる。

$\dfrac{\pi}{2}<\theta\leq \pi$のとき、体積は負になるので、

$$V=|\mathbf{a}\cdot( \mathbf{b} \times \mathbf{c})|$$

となる。