スカラーをベクトルで微分したときの公式の証明について

- 1. スカラーをベクトルで微分する
- 2. スカラーをベクトルで微分したときの公式
- 3. 公式の証明
- 3.1. \(\frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{x}) = \mathbf{a}\)
- 3.2. \(\frac{\partial}{\partial \mathbf{x}} (\mathbf{x} \cdot \mathbf{x}) = 2\mathbf{x}\)
- 3.3. \(\frac{\partial}{\partial \mathbf{x}} \left( (\mathbf{x} – \mathbf{a})^T (\mathbf{x} – \mathbf{a}) \right) = 2(\mathbf{x} – \mathbf{a})\)
- 3.4. \(\frac{\partial}{\partial \mathbf{x}} (\mathbf{x}^T A \mathbf{x}) = (A + A^T) \mathbf{x}\)
- 4. 関連した記事
1. スカラーをベクトルで微分する
$$ \dfrac{\partial f}{\partial \mathbf{x}} = \left( \dfrac{\partial f}{\partial x_1} , \dfrac{\partial f}{\partial x_2} , \cdots \dfrac{\partial f}{\partial x_n} \right) $$
勾配ベクトル が得られます。これは、各変数に関する偏微分を集めたベクトルです。
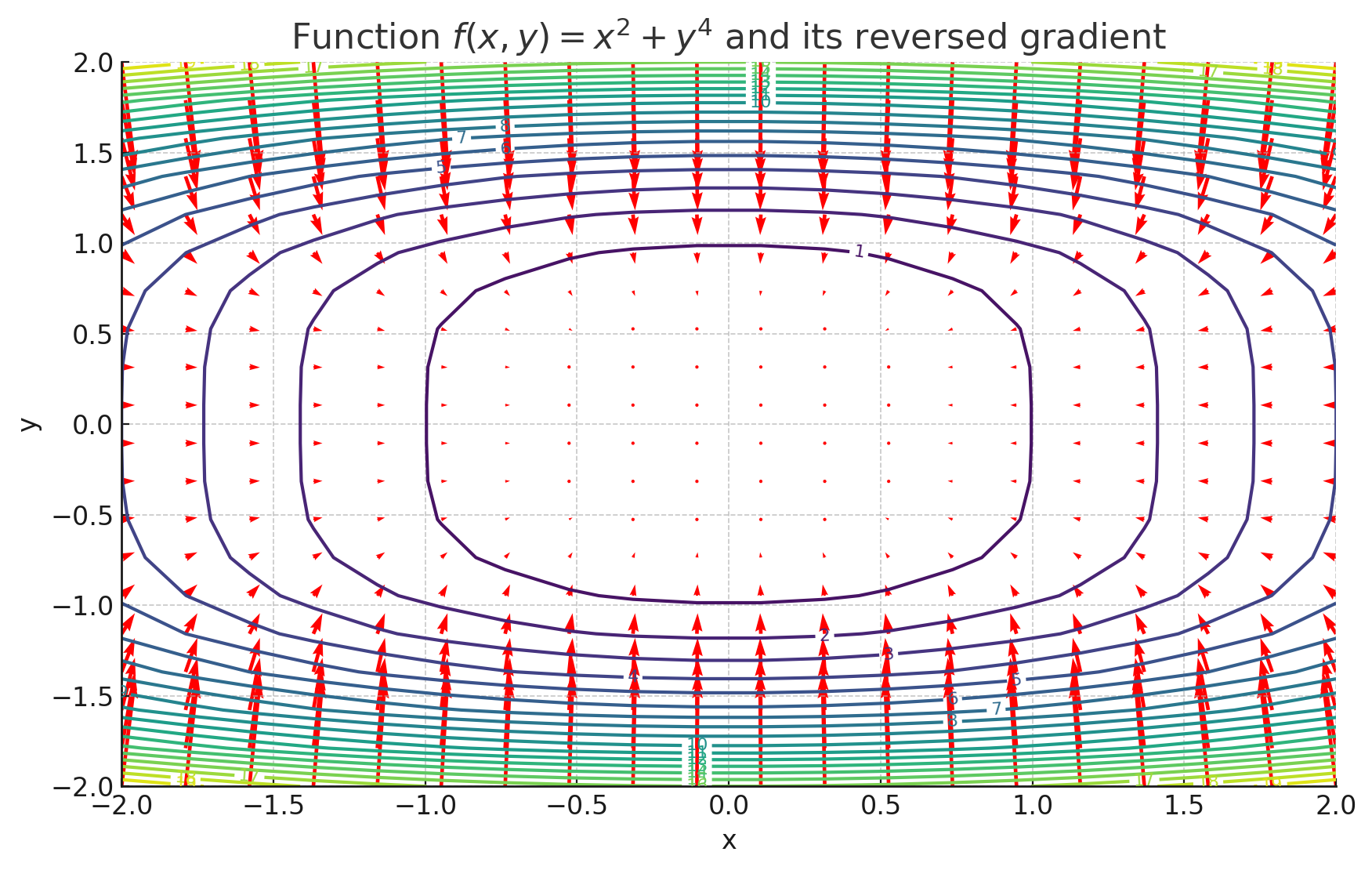
2. スカラーをベクトルで微分したときの公式
\[\begin{align*} \frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{x}) =\frac{\partial}{\partial \mathbf{x}}(\mathbf{x} \cdot \mathbf{a})&= \mathbf{a} \\ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x} \cdot \mathbf{x}) &= 2\mathbf{x}\\ \frac{\partial}{\partial \mathbf{x}} \left( (\mathbf{x} – \mathbf{a})^T (\mathbf{x} – \mathbf{a}) \right) &= 2(\mathbf{x} – \mathbf{a}) \\ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x}^T A \mathbf{x}) &= (A + A^T) \mathbf{x} \end{align*}\]
3. 公式の証明
3.1. \(\frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{x}) = \mathbf{a}\)
まず、スカラー積の微分について考えます。スカラー積は次のように展開されます。 \[ \mathbf{a} \cdot \mathbf{x} = \sum_{i=1}^n a_i x_i \] これを各成分で微分すると、以下のようになります。 \[ \frac{\partial}{\partial x_j} (\mathbf{a} \cdot \mathbf{x}) = \frac{\partial}{\partial x_j} \left( \sum_{i=1}^n a_i x_i \right) = a_j \] したがって、ベクトルとしてまとめると、 \[ \frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{x}) = \mathbf{a} \] です。
3.2. \(\frac{\partial}{\partial \mathbf{x}} (\mathbf{x} \cdot \mathbf{x}) = 2\mathbf{x}\)
次に、ベクトルの内積を考えます。内積は以下のように表せます。 \[ \mathbf{x} \cdot \mathbf{x} = \sum_{i=1}^n x_i^2 \] これを成分ごとに微分すると、 \[ \frac{\partial}{\partial x_j} (\mathbf{x} \cdot \mathbf{x}) = \frac{\partial}{\partial x_j} \left( \sum_{i=1}^n x_i^2 \right) = 2x_j \] よって、ベクトルとしてまとめると、 \[ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x} \cdot \mathbf{x}) = 2\mathbf{x} \] です。
3.3. \(\frac{\partial}{\partial \mathbf{x}} \left( (\mathbf{x} – \mathbf{a})^T (\mathbf{x} – \mathbf{a}) \right) = 2(\mathbf{x} – \mathbf{a})\)
まず、この式を展開します。 \[ (\mathbf{x} – \mathbf{a})^T (\mathbf{x} – \mathbf{a}) = (\mathbf{x} \cdot \mathbf{x}) – 2(\mathbf{a} \cdot \mathbf{x}) + (\mathbf{a} \cdot \mathbf{a}) \] これをそれぞれ微分すると、すでに示した結果を用いて次のようになります。 \[ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x} \cdot \mathbf{x}) = 2\mathbf{x}, \quad \frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{x}) = \mathbf{a}, \quad \frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{a}) = 0 \] これらをまとめると、 \[ \frac{\partial}{\partial \mathbf{x}} \left( (\mathbf{x} – \mathbf{a})^T (\mathbf{x} – \mathbf{a}) \right) = 2\mathbf{x} – 2\mathbf{a} = 2(\mathbf{x} – \mathbf{a}) \] です。
3.4. \(\frac{\partial}{\partial \mathbf{x}} (\mathbf{x}^T A \mathbf{x}) = (A + A^T) \mathbf{x}\)
この項は少し複雑ですが、まず行列 \( A \) が一般の \( n \times n \) 行列であるとします。以下のように展開できます。 \[ \mathbf{x}^T A \mathbf{x} = \sum_{i=1}^n \sum_{j=1}^n x_i A_{ij} x_j \] これを成分 \( x_k \) について微分すると、 \[ \frac{\partial}{\partial x_k} \left( \sum_{i=1}^n \sum_{j=1}^n x_i A_{ij} x_j \right) = \sum_{j=1}^n A_{kj} x_j + \sum_{i=1}^n A_{ik} x_i \] つまり、次のようにまとめられます。 \[ \frac{\partial}{\partial x_k} (\mathbf{x}^T A \mathbf{x}) = \sum_{j=1}^n (A_{kj} + A_{jk}) x_j \] よって、ベクトル全体での微分は、 \[ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x}^T A \mathbf{x}) = (A + A^T) \mathbf{x} \] です。



