【scikit-learn】ガウス混合モデル（GMM）の意味と使い方について

はるか

ガウス混合モデル（GMM）って知ってる？

ふゅか

うん、データを複数の正規分布に分けることで全体の構造を見つけるモデルだよね！クラスタリングによく使われるやつ！

1. ガウス混合モデル（GMM）とは？

ガウス混合モデル（GMM）は、クラスタリングやデータ分布の分析で使われる統計モデルの一つです。データがいくつかの正規分布（ガウス分布）に従っていると仮定し、それらを組み合わせた形でデータ全体の分布を表現します。

2. ガウス混合モデルの特徴

2.1. 確率分布を基にしたモデル

GMMはデータを複数のガウス分布（正規分布）に分解し、それぞれの分布の平均と分散を見つけます。

2.2. 楕円形のクラスタリング

k-meansのようなクラスタリング手法と異なり、GMMはクラスタの形を楕円形でモデル化できます。このため、非対称や異なる大きさのクラスタにも対応可能です。

3. Scikit-learnのガウス混合モデル（GMM）の使い方

3.1. 実装の基本手順

以下は、Scikit-learnでGMMを使用してクラスタリングを実行する流れです。

3.2. コード例

from sklearn.mixture import GaussianMixture
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# データセットの生成
iris = load_iris()
X, y = iris.data, iris.target
# ガウス混合モデルの初期化と学習
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(X)

# 各データ点のクラスタを予測
labels = gmm.predict(X)


# ガウス分布の中心点（平均）
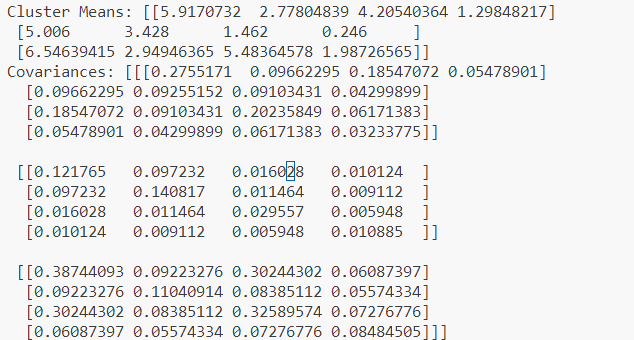
print("Cluster Means:", gmm.means_)

# クラスタの分散（共分散行列）
print("Covariances:", gmm.covariances_)

今回の場合は、平均と分散共分散行列は次のようになりました。

3.3. クラスタリングの評価

from sklearn.metrics import adjusted_rand_score, normalized_mutual_info_score, silhouette_score

# Adjusted Rand Index
ari = adjusted_rand_score(y, labels)
print(f"Adjusted Rand Index (ARI): {ari:.3f}")

# Normalized Mutual Information
nmi = normalized_mutual_info_score(y, labels)
print(f"Normalized Mutual Information (NMI): {nmi:.3f}")

# Silhouette Score
sil_score = silhouette_score(X, labels)
print(f"Silhouette Score: {sil_score:.3f}")

• Adjusted Rand Index (ARI)
  • 値の範囲は[-1, 1]（通常は0から1）。1に近いほど真のラベルと一致しています。
• Normalized Mutual Information (NMI)
  • 値の範囲は[0, 1]。1に近いほど真のラベルとの一致度が高いです。
• Silhouette Score
  • 値の範囲は[-1, 1]。1に近いほど、データポイントが適切なクラスタに属しています。
  • 負の値の場合はクラスタリングが不適切であることを示します。

結果は次のようになりました。ARIとNMIが1に近いので、真のラベルと一致率が高いことがわかります。