【scikit-learn】主成分分析（PCA）の意味と使い方について

はるか

PCAって、次元削減の一種だよね。データを小さくしても特徴を保つ手法。

ふゅか

そう！例えば、4次元のデータを2次元にしても、意味のある情報がちゃんと残るの！グラフとか作るのに便利よね！

1. 主成分分析（PCA）

主成分分析（PCA: Principal Component Analysis）は、高次元データを低次元に圧縮しながら、データの特徴を最大限に保持するための手法です。データの可視化や次元削減、ノイズ除去などに利用され、特に機械学習やデータ分析の前処理でよく使われます。

1.1. 直感的なイメージ

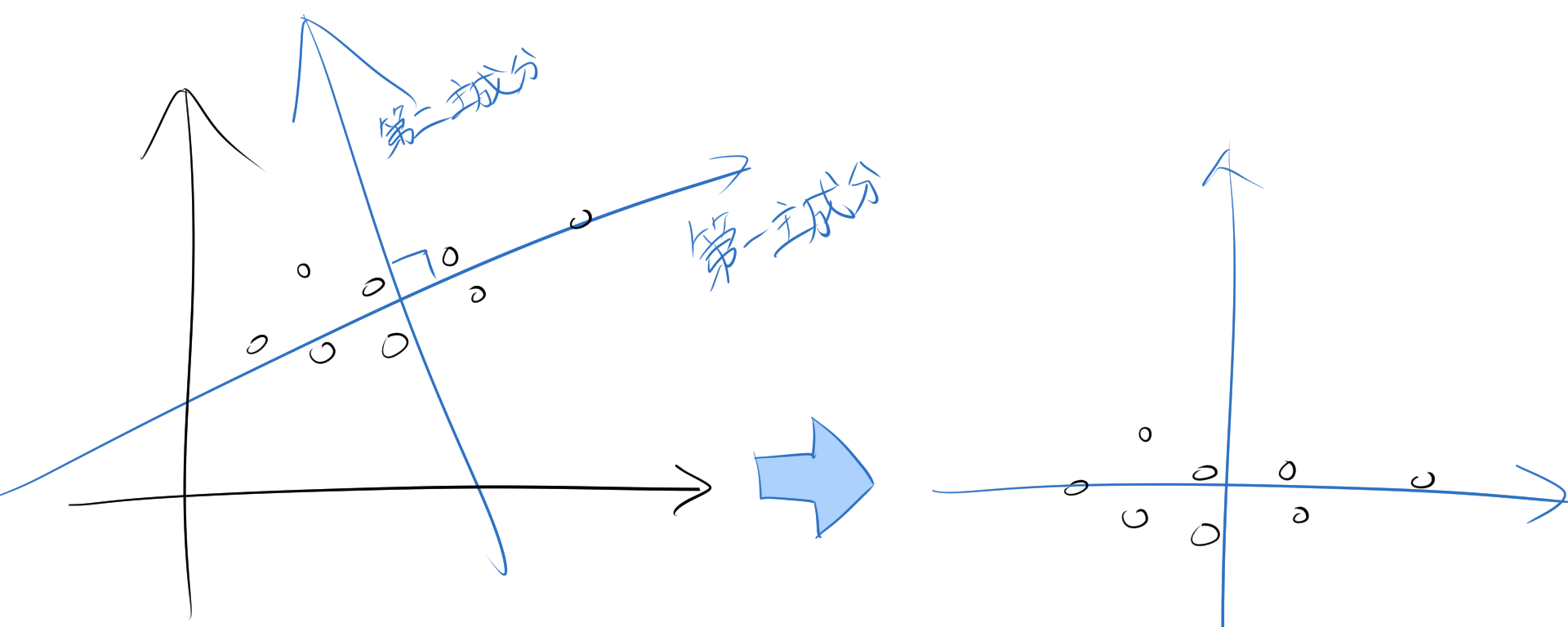
データの中には、特に情報が多く含まれる方向（主成分）があります。PCAは、その情報ができるだけ失わない方向を見つけて、その方向を「軸」としてデータを再配置します。

主成分分析は特に、この新しい軸の解釈が難しいといわれています。

ふゅか

でも、PCAの「情報が多く含まれる方向」って、どうやって見つけるの？

はるか

実際には、固有値を計算するけど、直感的には図みたいな感じ。

2. Scikit-learnでのPCAの実装方法

Scikit-learnを使うと、これらの複雑な手順を簡単に実行できます。以下に具体的な例を示します。

2.1. 必要なライブラリをインポート

まず、PCAの実装に必要なライブラリをインポートします。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
import japanize_matplotlib

japanize_matplotlibは次のmatplotlibの日本語の文字化け解消の記事で解説しています。

2.2. データの読み込みと前処理

次に、データを読み込み、標準化します。今回はtoyデータセットであるIrisデータセットを使用します。このデータセットには、花の種類に対応する特徴量とラベルが含まれています。

# データセットの読み込み（Irisデータセットを使用）
data = load_iris()
X = data.data  # 特徴量
y = data.target  # クラスラベル

# データの標準化（平均0、分散1）
scaler = StandardScaler()
X_standardized = scaler.fit_transform(X)

標準化を行う理由は、PCAがデータのスケールに敏感であるためです。

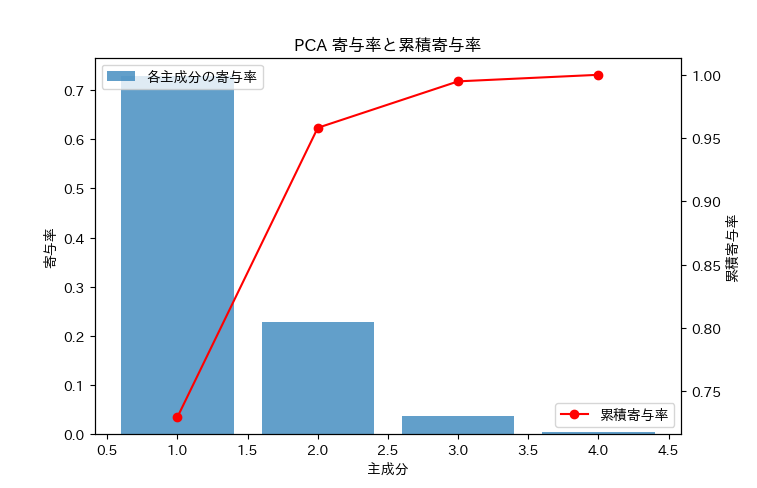
2.3. 寄与率

PCA（主成分分析）で寄与率を見ることで、各主成分がデータの情報をどの程度保持しているかを確認できます。

# PCAの実行
pca = PCA(n_components=4)
pca.fit(X_standardized)
X_pca = pca.transform(X_standardized)

# 寄与率の取得
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)

# グラフの描画
fig, ax1 = plt.subplots()

# 主成分ごとの寄与率
ax1.bar(range(1, len(explained_variance_ratio) + 1), explained_variance_ratio, alpha=0.7, label='各主成分の寄与率')
ax1.set_xlabel('主成分')
ax1.set_ylabel('寄与率')
ax1.set_title('PCA 寄与率と累積寄与率')

# 累積寄与率の描画
ax2 = ax1.twinx()
ax2.plot(range(1, len(cumulative_variance_ratio) + 1), cumulative_variance_ratio, marker='o', color='red', label='累積寄与率')
ax2.set_ylabel('累積寄与率')

# 凡例の追加
ax1.legend(loc='upper left')
ax2.legend(loc='lower right')

plt.show()

一般的に累積寄与率が80%程度で、主成分を抽出するというこが目安となっています。

グラフと累積寄与率から、2次元で十分にデータを表現できることがわかります。

ふゅか

累積寄与率が80%って、どんな意味があるの？

はるか

80%の情報がその主成分に含まれているってこと。それだけで十分にデータを表現可能。

2.4. PCAの適用

PCAを使用して、データを2次元に圧縮します。

# PCAを適用して次元削減
pca = PCA(n_components=2)  # 主成分を2次元に圧縮
X_pca = pca.fit_transform(X_standardized)

# 主成分の分散比率（重要度の割合）を表示
print("寄与率:", pca.explained_variance_ratio_)

ここでのn_components=2は、次元を2に圧縮することを意味します。

はるか

主成分2つに圧縮したら、特徴量は2次元になる。

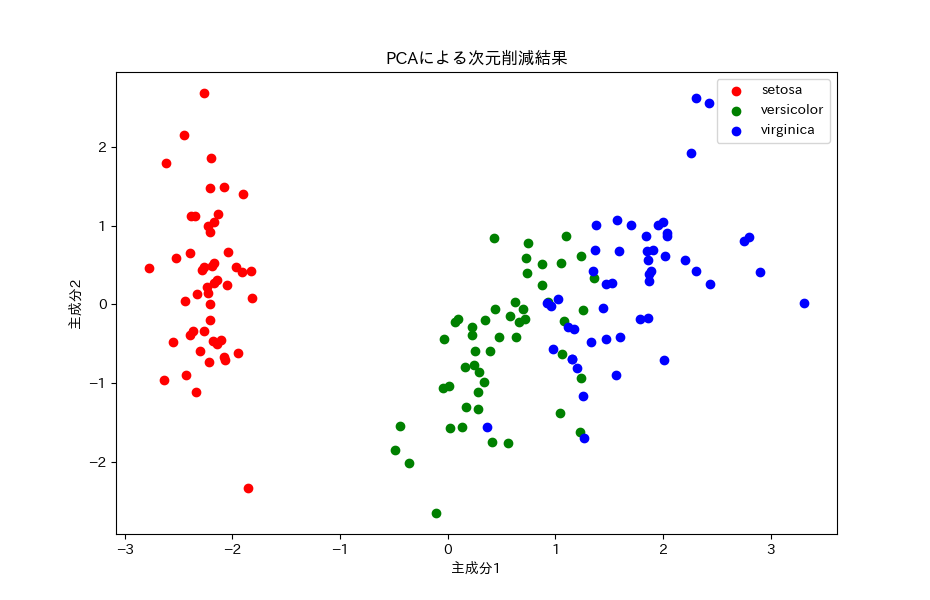
2.5. 結果の可視化

最後に、PCAで次元削減されたデータを散布図でプロットします。

# 結果をプロット
plt.figure(figsize=(8, 6))
for label, color in zip(np.unique(y), ['r', 'g', 'b']):
    plt.scatter(X_pca[y == label, 0], X_pca[y == label, 1], label=data.target_names[label], color=color)
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.legend()
plt.title('PCAによる次元削減結果')
plt.show()

もともと、4次元データでしたが、次のように2次元データでグラフをプロットできました。