更新:2024/07/25
Pythonで特殊関数を計算・プロットしよう!SciPyを使ったガンマ関数からルジャンドル関数まで
はるか
今日はPythonでSciPyを使った特殊関数の計算とプロットについて話す。
ふゅか
特殊関数って、数学や物理でよく使われる関数よね!
目次
1. SciPyで特殊関数
Pythonで特殊関数を出力するためにSciPyを使用します。特殊関数とは、数学や物理学においてよく使用される関数で、ガンマ関数、ベッセル関数、ベータ関数、誤差関数などが含まれます。それぞれの特殊関数のPythonコードを分けて、説明を追加します。
ふゅか
SciPyって便利なライブラリね!Pythonで特殊関数を計算するのに使えるなんて!
はるか
例えばガンマ関数の計算も簡単。
2. Pythonプログラム
2.1. scipyのinstall
まず、SciPyライブラリをインストールします。以下のコマンドを使用します。
pip install scipy2.2. ガンマ関数
ガンマ関数 \(\Gamma(z)\) は次のように定義されます。
\[ \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt \]
\[ \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt \]
ガンマ関数は、階乗に関連がある関数です。SciPyのscipy.specialモジュールを使用して計算します。gammaメソッドを呼び出すことで計算ができます。
import scipy.special as sp
# ガンマ関数の計算
gamma_value = sp.gamma(5)
print(f"Gamma(5) = {gamma_value}")Gamma(5) = 24.0ふゅか
例えば、Gamma(5)の計算はこんな感じね!
2.3. ベータ関数
ベータ関数 \(B(x, y)\) は次のように定義されます。
\[ B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1} \, dt \]
または
\[ B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)} \]
\[ B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1} \, dt \]
または
\[ B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)} \]
ベータ関数は、ガンマ関数を使用して定義される関数です。betaメソッドを呼び出すことで計算ができます。
import scipy.special as sp
# ベータ関数の計算
beta_value = sp.beta(2, 3)
print(f"Beta(2, 3) = {beta_value}")
Beta(2, 3) = 0.08333333333333333ふゅか
Beta(2, 3)の計算も簡単にできるのね!
2.4. エアリー関数
エアリー関数 \( \text{Ai}(x) \) と \( \text{Bi}(x) \) は次のように定義されます。
\[ \text{Ai}(x) = \frac{1}{\pi} \int_0^\infty \cos\left(\frac{t^3}{3} + xt\right) \, dt \]
\[ \text{Bi}(x) = \frac{1}{\pi} \int_0^\infty \left[ \exp\left(-\frac{t^3}{3} + xt\right) + \sin\left(\frac{t^3}{3} + xt\right) \right] dt \]
\[ \text{Ai}(x) = \frac{1}{\pi} \int_0^\infty \cos\left(\frac{t^3}{3} + xt\right) \, dt \]
\[ \text{Bi}(x) = \frac{1}{\pi} \int_0^\infty \left[ \exp\left(-\frac{t^3}{3} + xt\right) + \sin\left(\frac{t^3}{3} + xt\right) \right] dt \]
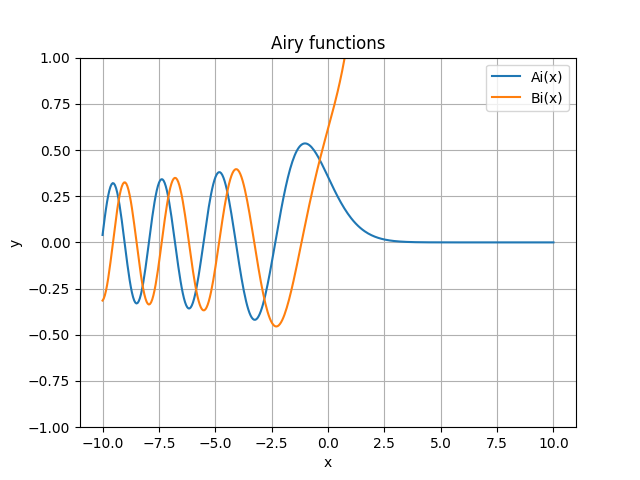
エアリー関数は、線形微分方程式の解として現れる関数です。Ai(x)とBi(x)を計算してグラフにプロットします。airyメソッドを呼ぶことで計算することができます。
import scipy.special as sp
import numpy as np
import matplotlib.pyplot as plt
# エアリー関数の計算とプロット
x = np.linspace(-10, 10, 400)
ai, aip, bi, bip = sp.airy(x)
plt.plot(x, ai, label='Ai(x)')
plt.plot(x, bi, label='Bi(x)')
plt.title("Airy functions")
plt.ylim(-1,1)
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.grid(True)
plt.show()
2.5. ベッセル関数(第二種、第三種)
第二種ベッセル関数 \(Y_\nu(x)\) と第三種ベッセル関数 \(K_\nu(x)\) は次のように定義されます。
第二種ベッセル関数
\[ Y_\nu(x) = \frac{J_\nu(x) \cos(\nu \pi) – J_{-\nu}(x)}{\sin(\nu \pi)} \]
第三種ベッセル関数(修正ベッセル関数)
\[ K_\nu(x) = \frac{\pi}{2} \frac{I_{-\nu}(x) – I_\nu(x)}{\sin(\nu \pi)} \]
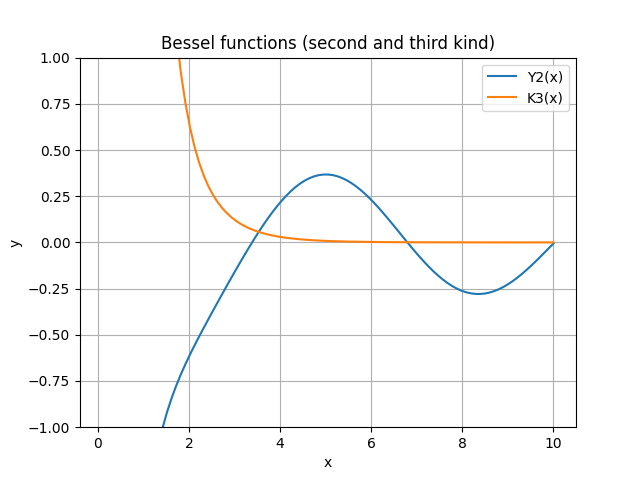
ベッセル関数は、波動方程式の解として現れる関数です。ここでは第二種と第三種のベッセル関数を計算して、グラフにプロットします。yvとkvメソッドを呼ぶことで計算することができます。
import scipy.special as sp
import numpy as np
import matplotlib.pyplot as plt
# ベッセル関数の計算とプロット
x = np.linspace(0, 10, 100)
y2 = sp.yv(2, x) # 第二種ベッセル関数
y3 = sp.kv(3, x) # 第三種ベッセル関数(修正ベッセル関数)
plt.plot(x, y2, label='Y2(x)')
plt.plot(x, y3, label='K3(x)')
plt.title("Bessel functions (second and third kind)")
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-1,1)
plt.legend()
plt.grid(True)
plt.show()
2.6. ゼータ関数
リーマンゼータ関数 \(\zeta(s)\) は次のように定義されます。
\[ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} \]
解析接続により次の積分表示もあります。
\[ \zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^t – 1} \, dt \]
\[ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} \]
解析接続により次の積分表示もあります。
\[ \zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^t – 1} \, dt \]
リーマンゼータ関数は、解析数論で重要な役割を果たします。zetaメソッドを呼ぶことで計算することができます。
import scipy.special as sp
# ゼータ関数の計算
zeta_value_2 = sp.zeta(2)
zeta_value_m_2 = sp.zeta(-2)
print(f"Zeta(2) = {zeta_value_2}")
print(f"Zeta(-2) = {zeta_value_m_2}")Zeta(2) = 1.6449340668482264
Zeta(-2) = 0.02.7. 楕円関数
楕円積分の第一種 \(K(k)\) と第二種 \(E(k)\) は次のように定義されます。
第一種完全楕円積分
\[ K(k) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{\sqrt{1 – k^2 \sin^2(\theta)}} \]
第二種完全楕円積分
\[ E(k) = \int_0^{\frac{\pi}{2}} \sqrt{1 – k^2 \sin^2(\theta)} \, d\theta \]
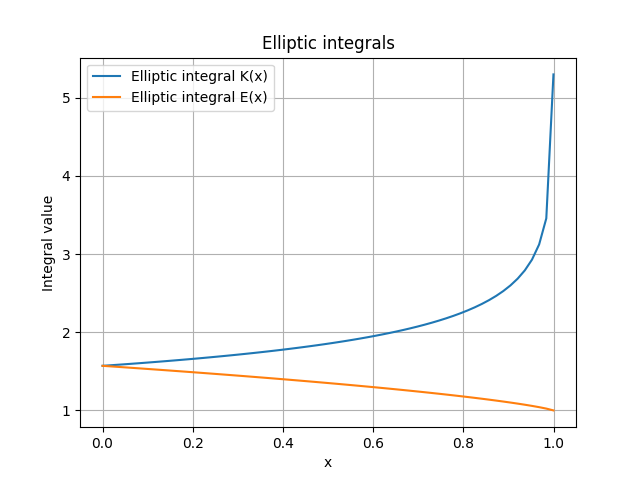
楕円積分は、楕円関数や楕円運動に関連する積分です。ellipe,ellipkメソッドを呼ぶことで計算することができます。
import scipy.special as sp
import numpy as np
import matplotlib.pyplot as plt
# 楕円積分の計算とプロット
x = np.linspace(0, np.pi/2, 100)
ellipk_value = sp.ellipk(x)
ellipe_value = sp.ellipe(x)
plt.plot(x, ellipk_value, label='Elliptic integral K(x)')
plt.plot(x, ellipe_value, label='Elliptic integral E(x)')
plt.title("Elliptic integrals")
plt.xlabel("x")
plt.ylabel("Integral value")
plt.legend()
plt.grid(True)
plt.show()
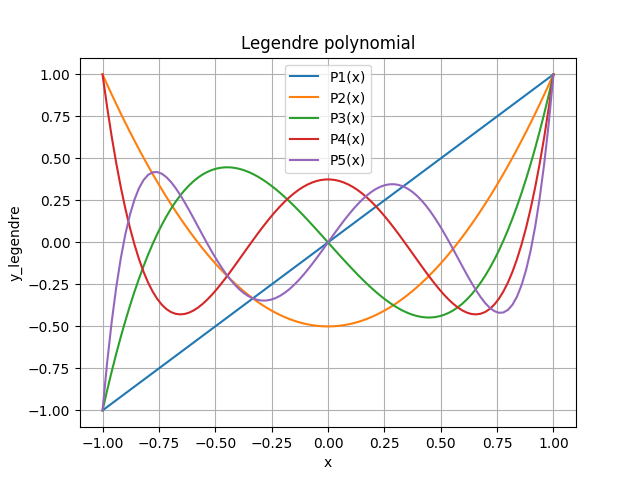
2.8. ルジャンドル関数
ルジャンドル多項式 \(P_n(x)\) は次のように定義されます。
\[ P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 – 1)^n\right] \]
\[ P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 – 1)^n\right] \]
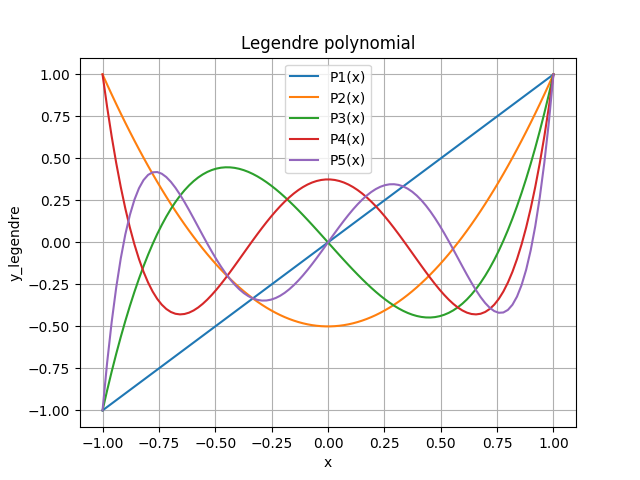
ルジャンドル多項式は、球面調和関数などの特殊関数に現れます。
ふゅか
最後にnを1~5まで変えたグラフを見てみよう!
import scipy.special as sp
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 100)
for i in range(1,6):
# ルジャンドル多項式の計算とプロット
legendre_p = sp.legendre(i)
y_legendre = legendre_p(x)
plt.plot(x, y_legendre, label=f'P{i}(x)')
plt.title("Legendre polynomial")
plt.xlabel("x")
plt.ylabel("y_legendre")
plt.legend()
plt.grid(True)
plt.show()
PR