
はるか
数列の和を考えるとき、差分を取るとシグマがシンプルになることがある。

ふゅか
そうね!例えば、和の差分を取ると
f(n+1)−f(0)だけが残るのよね♪
1. 差分
数列の和の差分を取ったとき以下のような関係式が成り立つ。
k=0∑nf(k+1)−f(k)=f(n+1)−f(0)
1.1. 差分の仕組み

はるか
打ち消しあうことで、残る部分が
f(n+1)−f(0)になる。

ふゅか
その通り♪ 画像を見て、差分がどう打ち消しあうか確認してね!
以下のように足し合わせた結果、打ち消しあって、残った部分が
f(n+1)−f(0)となります。
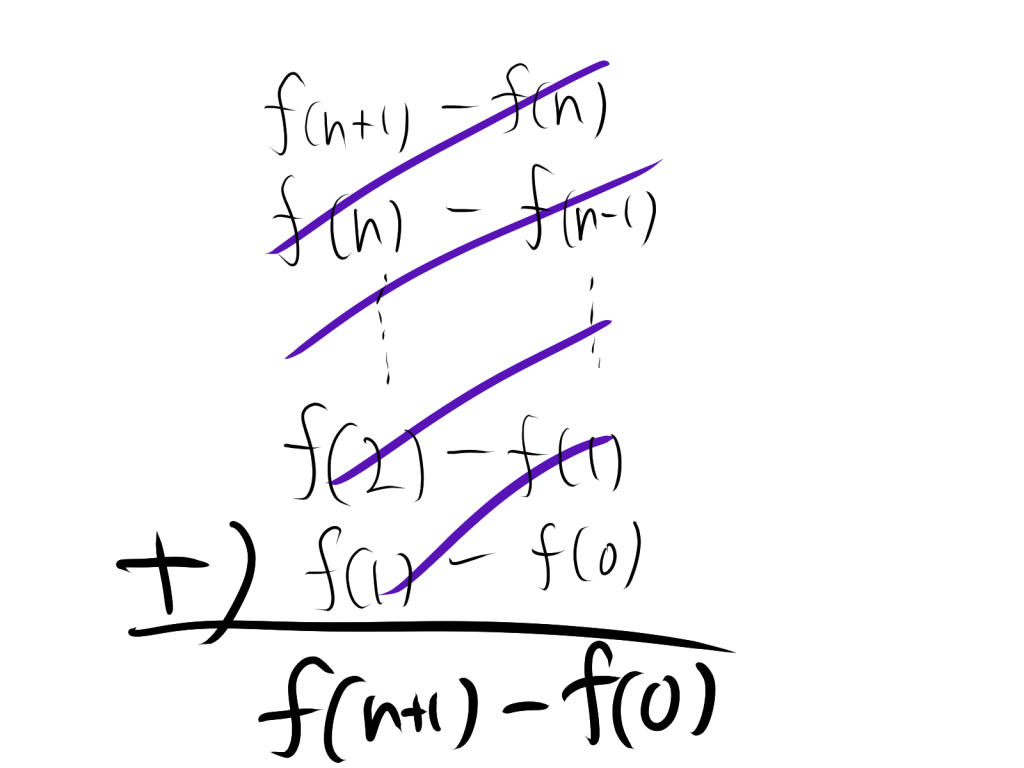
たとえば、k=1∑nf(k+1)−f(k)となったときに、同じ考え方で計算すると、以下のようになります。
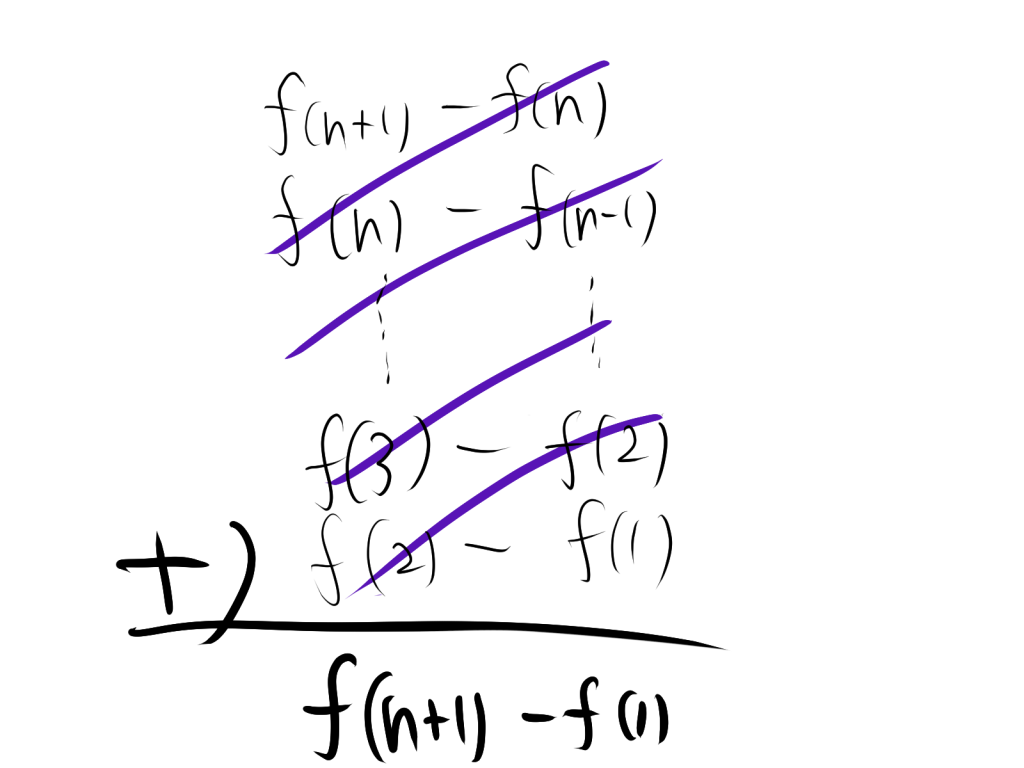
2. 例題
以下の数列の和を計算せよ。
(1)k=0∑n2k
(2)k=0∑n3k⋅2k
(3)k=1∑nk(k+2)1
(1)まずは、ウォーミングアップです。これは通常は等比数列の和で考えてもよいのですが差分で考えると以下のようになります。
k=0∑n2k
=k=0∑n2⋅2k−1
=k=0∑n(4−2)2k−1
=k=0∑n4⋅2k−1−2⋅2k−1
=k=0∑n2k+1−2k
=2n+1−1
となります。
(2)コツは、f(n)の形を予想するということです。f(k)=(ak+b)⋅2kであると予想します。
f(k+1)−f(k)={a(k+1)+b}2k+1−(ak+b)2k
=(ak+2a+b)2k
f(k+1)−f(k)=3k⋅2kとなるから、恒等式より、
ak=3k
2a+b=0
であることがわかるから、a=3,b=−6である。
f(k)=(3k−6)2kとおくと、
k=0∑nf(k+1)−f(k)
={3(n+1)−6}2n+1−(−6)
=3(n−1)2n+1+6
(3)k(k+2)1に部分分数分解を行うと
k(k+2)1=21(k1−k+21)
また、式変形を行うと、
=−21(k+21−k1)
=−21(k+21+k+11−k+11−k1)
となる。f(k)=k+11+k1とおくと、
k=1∑nk(k+2)1
=−21k=1∑nf(k+1)−f(k)
=−21(n+21+n+11−23)

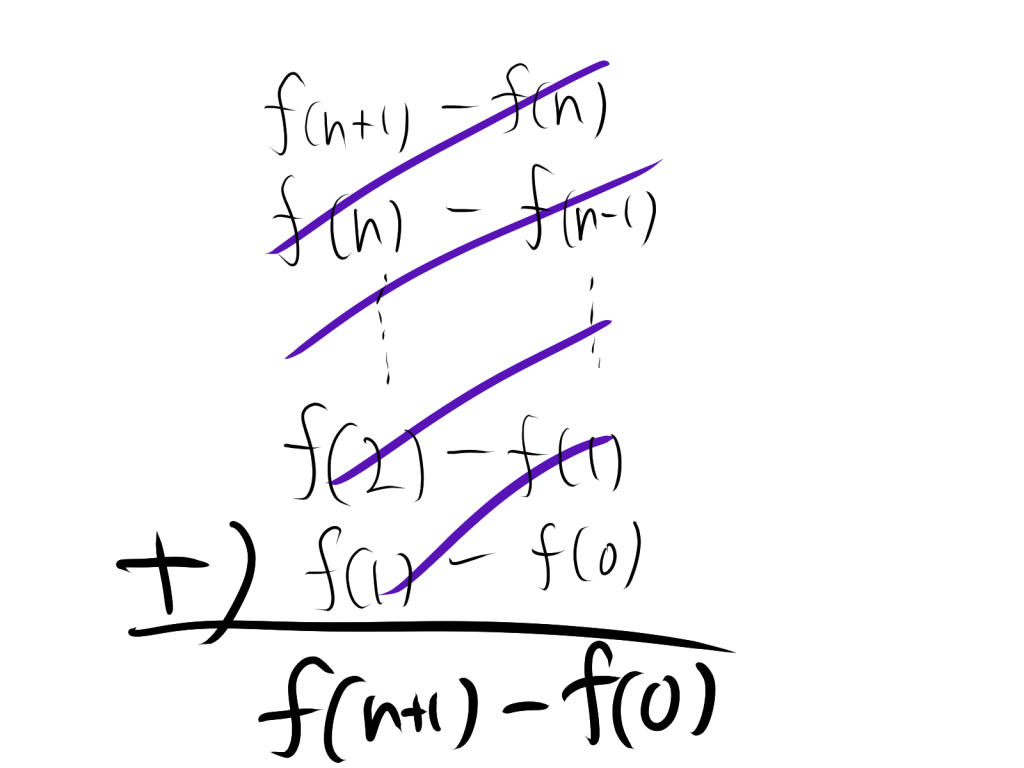
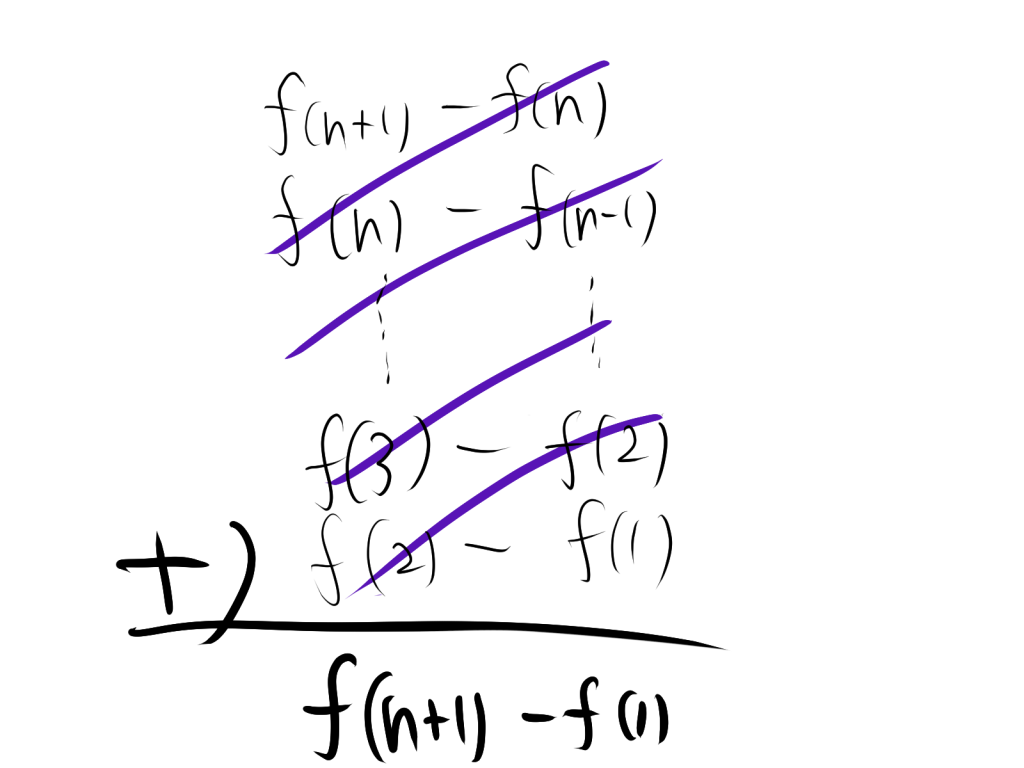

-e1727156598416.png.webp)


