【図解】正弦定理の意味と3つの証明について

1. 正弦定理
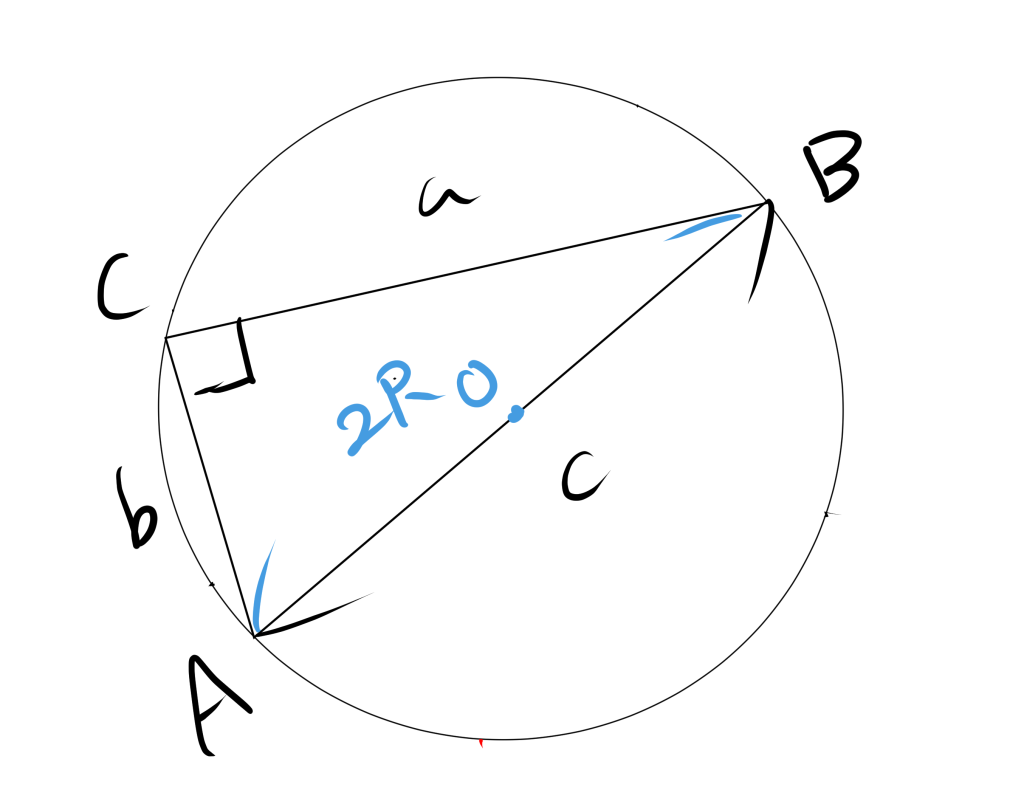
$$\dfrac{a}{\sin\mathrm{A}}=\dfrac{b}{\sin\mathrm{B}}=\dfrac{c}{\sin\mathrm{C}}=2R$$
ここで、三角形$ABC$について、辺$AB$の長さを$c$、辺$BC$の長さを$a$、辺$CA$の長さを$b$、三角形$ABC$の外接円の半径を$R$とする。
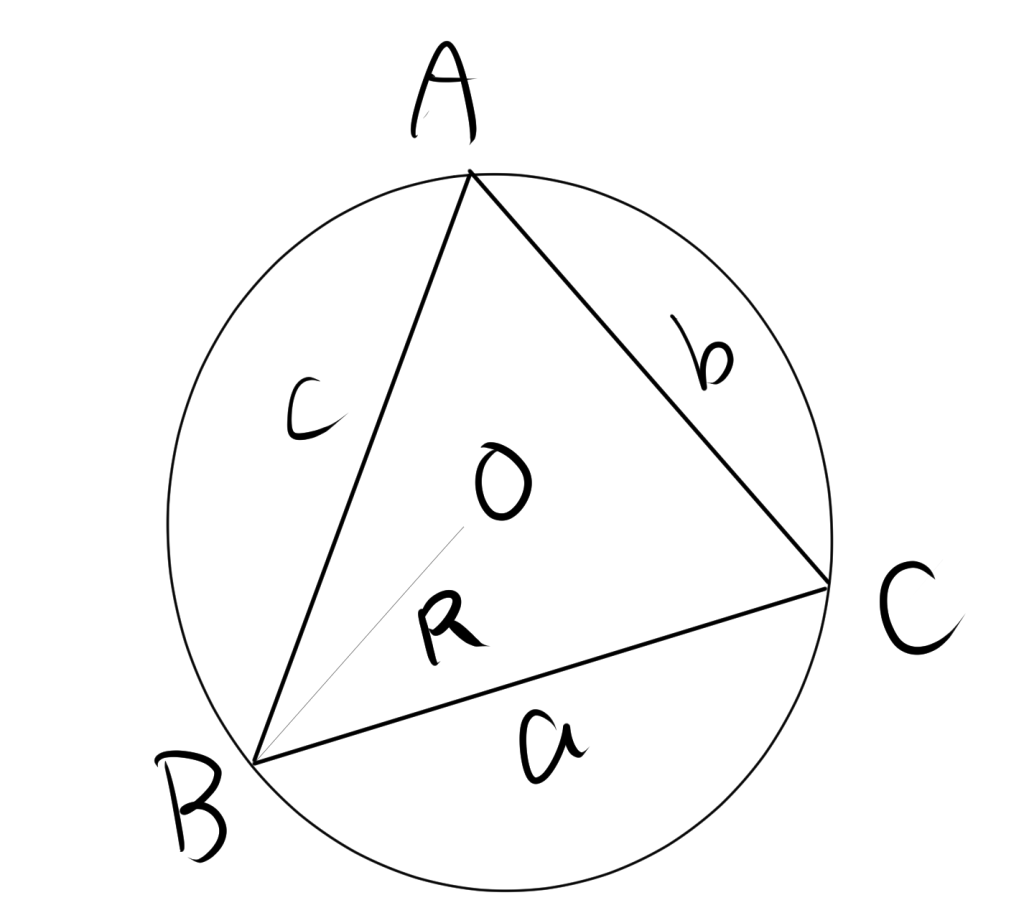
2. 証明
2.1. 円周角の定理を用いた証明
角$C$が鋭角、直角、鈍角の場合に分けて証明を行う。
$[1]$角$C$が鋭角であるとき
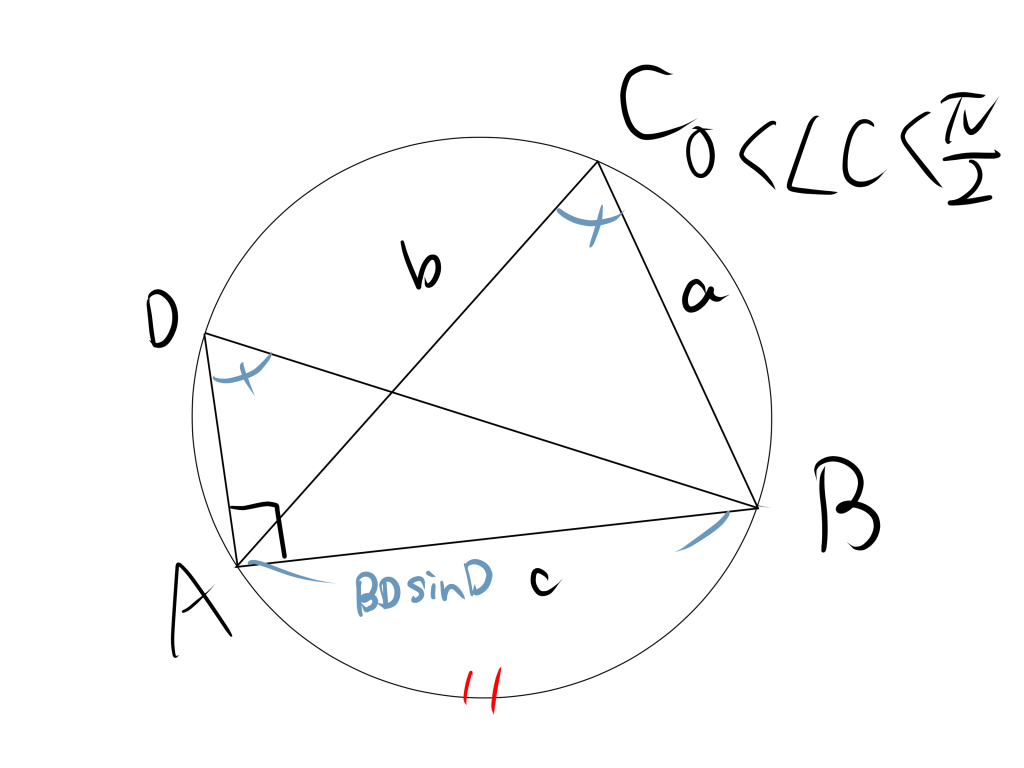
三角形$ABC$について、辺$AB$の長さを$c$、辺$BC$の長さを$a$、辺$CA$の長さを$b$、三角形$ABC$の外接円の半径を$R$とする。とする。角Aから外接円に対して垂線を引いた時の交点をDとする。その時、直角であるときの円周角の定理より、BDの長さは直径となるため、$BD=2R$となる。よって、三角比を用いると、
$$c=\mathrm{BD}\sin\mathrm{D}$$
$$c=\mathrm{2R}\sin\mathrm{D}$$
となる。一方で円周角の定理より、$\angle C = \angle D$であるから、
$$c=\mathrm{2R}\sin\mathrm{D}$$
$$c=\mathrm{2R}\sin\mathrm{C}$$
$$\therefore \dfrac{c}{\sin\mathrm{C}}=\mathrm{2R}$$
$[2]$角$C$が直角であるとき
角Cが直角$\angle \mathrm{C}=\dfrac{\pi}{2}$であるから、ABが外接円の直径となるため、$c=2R$となる。$\sin\dfrac{\pi}{2}=1$であるから、$\sin\mathrm{C}=1$となる。したがって、
$$c=\mathrm{2R}$$
$$\dfrac{c}{\sin\mathrm{C}}=\mathrm{2R}$$
$[2]$角$C$が鈍角であるとき
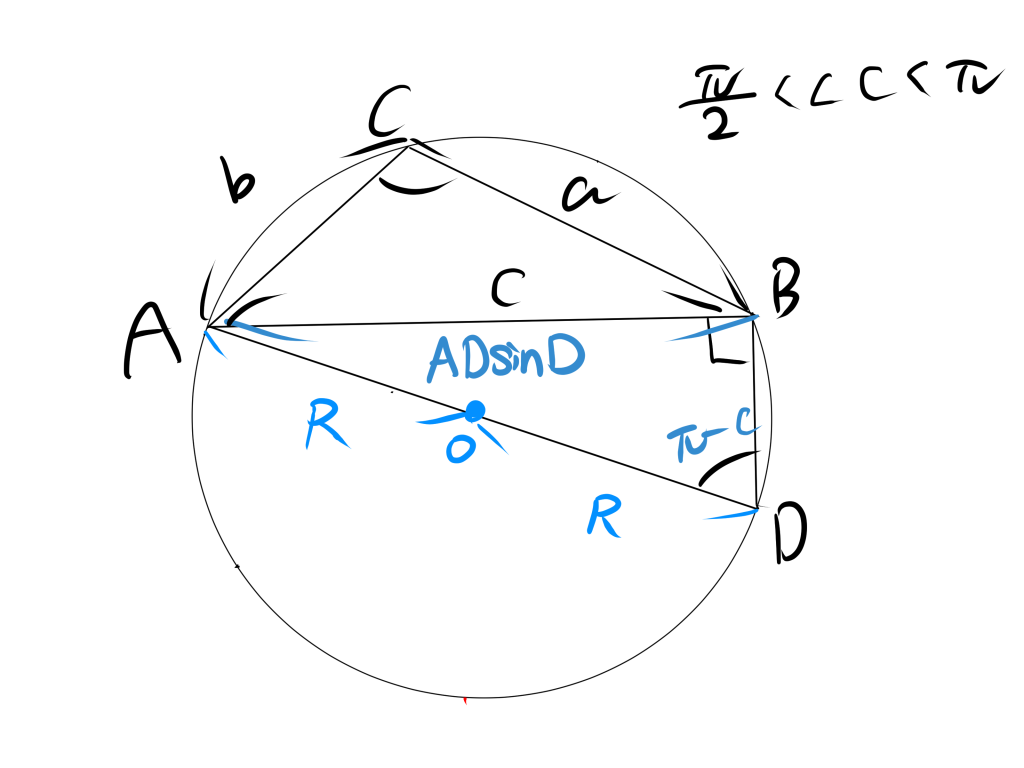
角$B$から外接円に対して垂線を引いた時の交点を$D$とする。その時、直角であるときの円周角の定理より、$AD$の長さは直径となるため、$AD=2R$となる。よって、三角比を用いると、
$$c=\mathrm{AD}\sin\mathrm{D}$$
$$c=\mathrm{2R}\sin\mathrm{D}$$
$\angle C=\pi-\angle D$であるから、$\sin\mathrm{C}=\sin\mathrm{D}$となるため、
$$c=\mathrm{2R}\sin\mathrm{c}$$
$$\dfrac{c}{\sin\mathrm{C}}=\mathrm{2R}$$
となる。
[1],[2],[3]より、角Cについて、$\dfrac{c}{\sin\mathrm{C}}=\mathrm{2R}$が成り立つことが示された。よって、角A,角Bについても同様にすることで、
$$\dfrac{a}{\sin\mathrm{A}}=\mathrm{2R}$$
$$\dfrac{b}{\sin\mathrm{B}}=\mathrm{2R}$$
が成り立つことがわかる。よって、以下の式が成り立つ。
$$\dfrac{a}{\sin\mathrm{A}}=\dfrac{b}{\sin\mathrm{B}}=\dfrac{c}{\sin\mathrm{C}}=2R$$
以下では、$\dfrac{a}{\sin\mathrm{A}}=\dfrac{b}{\sin\mathrm{B}}=\dfrac{c}{\sin\mathrm{C}}$という、外接円の半径を含まない式の証明を行います。
2.2. 余弦定理を用いた証明
余弦定理より、
$$\cos \mathrm{A}= \dfrac{b^2+c^2-a^2}{2bc}$$
であるから、$\sin^2\mathrm{A}=1-\cos^2\mathrm{A}$より、
$$\dfrac{a^2}{\sin^2\mathrm{A}}$$
$$=\dfrac{a^2}{1-\cos^2\mathrm{A}}$$
$$=\dfrac{a^2}{(1-\cos\mathrm{A})(1+\cos\mathrm{A})}$$
$$=\dfrac{a^2}{\left(1-\dfrac{b^2+c^2-a^2}{2bc}\right)\left(1+\dfrac{b^2+c^2-a^2}{2bc}\right)}$$
$$=\dfrac{4a^2b^2c^2}{\{2bc-(b^2+c^2-a^2)\}\{2bc+(b^2+c^2-a^2)\}}$$
$$=\dfrac{4a^2b^2c^2}{\{a^2-(b-c)^2\}\{(b+c)^2-a^2\}}$$
$$=\dfrac{4a^2b^2c^2}{(a-b+c)(a+b-c)(-a+b+c)(a+b+c)}$$
$\dfrac{b^2}{\sin^2\mathrm{B}}$、$\dfrac{c^2}{\sin^2\mathrm{C}}$についても同様の結果になる。そのため、$\sin\mathrm{A}>0,\sin\mathrm{B} >0 \sin C>0$より、
$$\dfrac{a}{\sin\mathrm{A}}=\dfrac{b}{\sin\mathrm{B}}=\dfrac{c}{\sin\mathrm{C}}$$
となる。
2.3. 面積を用いた証明
sinを用いた三角形の面積の求め方より、三角形の面積$S$は以下のようになる。
$$S=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B$$
$\dfrac{1}{2}ab\sin C=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B$であるから、等式に$abc\neq0$で割ると、
$$\dfrac{\sin\mathrm{C}}{2c}=\dfrac{\sin\mathrm{A}}{2a}=\dfrac{\sin\mathrm{B}}{2b}$$
$\sin\mathrm{A}>0,\sin\mathrm{B} >0 \sin C>0$より、式を2倍した後に、逆数をとると、
$$\dfrac{a}{\sin\mathrm{A}}=\dfrac{b}{\sin\mathrm{B}}=\dfrac{c}{\sin\mathrm{C}}$$