sinc関数の極限・積分・微分・グラフについて

1. sinc関数とは
sinc関数は、信号処理やフーリエ解析などで頻繁に登場する関数で、次のように定義されます。
\[ \text{sinc}(x) = \begin{cases} \dfrac{\sin( x)}{ x} & (x \neq 0) \\ 1 & (x = 0) \end{cases} \]
ここで、\( x = 0 \) の場合は、\(\displaystyle\lim_{x \to 0} \frac{\sin( x)}{ x}\) を計算すると 1 になるため、特に 1 と定義されます。
1.1. 偶関数
sinc関数は偶関数です。なぜなら、
\[ \text{sinc}(-x) = \frac{\sin(-x)}{-x} = \frac{-\sin(x)}{-x} = \frac{\sin(x)}{x} = \text{sinc}(x) \]
これにより、sinc関数のグラフは \( y \)軸に対して対称です。
2. sinc関数の極限
$$\lim_{x\to 0} \frac{\sin x}{x} = 1 $$
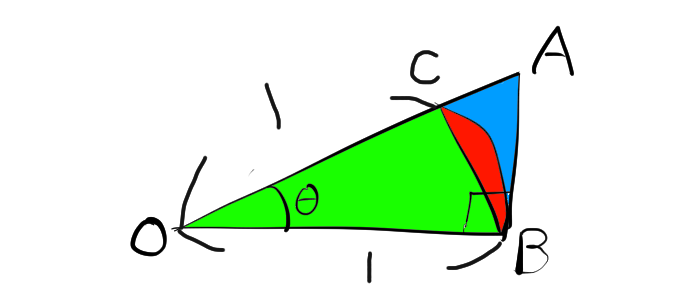
2.1. 面積を利用
$$二等辺三角形OCB<扇形OCB<三角形OAB$$
したがって、
$$\frac{1}{2}\sin \theta < \frac{1}{2}\theta < \frac{1}{2}\tan\theta$$
$\theta > 0$のとき、$\sin\theta$で割ると、次のようになる。
$$1 < \frac{\theta}{\sin\theta} < \frac{1}{\cos\theta}$$
$$\cos\theta < \frac{\sin\theta}{\theta} < 1$$
ここで、$\displaystyle\lim_{\theta\to +0}\cos\theta =1$となる。
したがって、$\theta\to +0$の極限ははさみうちの原理より、
$$\lim_{\theta\to +0}\frac{\sin\theta}{\theta}=1$$
次に、$\theta<0$の時のsinc関数の極限を考えると次のようになります。
$$\lim_{\theta\to -0}\frac{\sin\theta}{\theta}$$
$x= -\theta$と置くと、$x>0$であるから、
$$=\lim_{x\to +0}\frac{\sin (-x)}{-x}$$
sinc関数は偶関数であるため、
$$=\lim_{x\to +0}\frac{\sin (x)}{x}=1$$
したがって、sinc関数の極限は次のようになる。
$$\lim_{\theta \to 0}\frac{\sin\theta}{\theta}=1$$
2.2. ロピタルの定理を利用
ロピタルの定理を使用すると次のようになります。
\[ \lim_{x \to 0} \frac{\sin x}{x} = \lim_{x \to 0} \frac{\cos x}{1} = \cos 0 = 1 \]
2.3. マクローリン展開
マクローリン展開を利用すると極限は次のようになります。
\[ \sin x = x – \frac{x^3}{6} + \frac{x^5}{120} – \dots \]
したがって、
\[ \frac{\sin x}{x} = 1 – \frac{x^2}{6} + \frac{x^4}{120} – \dots \]
\( x \to 0 \) のとき、高次の項は無視できるため、極限値は1になります。
3. 微分
\[ \frac{d}{dx} \left( \frac{\sin x}{x} \right) = \frac{x \cos x – \sin x}{x^2} \]
sinc関数の微分は商の微分法を用いて求められます。
\[ \frac{d}{dx} \left( \frac{\sin x}{x} \right) = \frac{x (\sin x)’ – (x)’\sin x}{x^2} \]
\[ =\frac{x \cos x – \sin x}{x^2} \]
4. 積分
sinc関数の不定積分は初等関数では表せませんが、「正弦積分関数(Si関数)」を用いて表されます。
\[ \int \frac{\sin x}{x} \, dx = \text{Si}(x) + C \]
ここで、
\[ \text{Si}(x) = \int_0^x \frac{\sin t}{t} \, dt \]
また、重要な広義積分の結果として、
\[ \int_0^\infty \frac{\sin x}{x} \, dx = \frac{\pi}{2} \]
があります。この積分はディリクレ積分と呼ばれます。
5. グラフ
5.1. 極値
極値を求めるには、 \( \text{sinc}'(x) = 0 \) となる \( x \) を探します。
\[ x \cos(x) – \sin(x) = 0 \]
これを整理すると、
\[ x \cos(x) = \sin(x) \]
したがって、
\[ \tan(x) = x \]
5.2. プロット
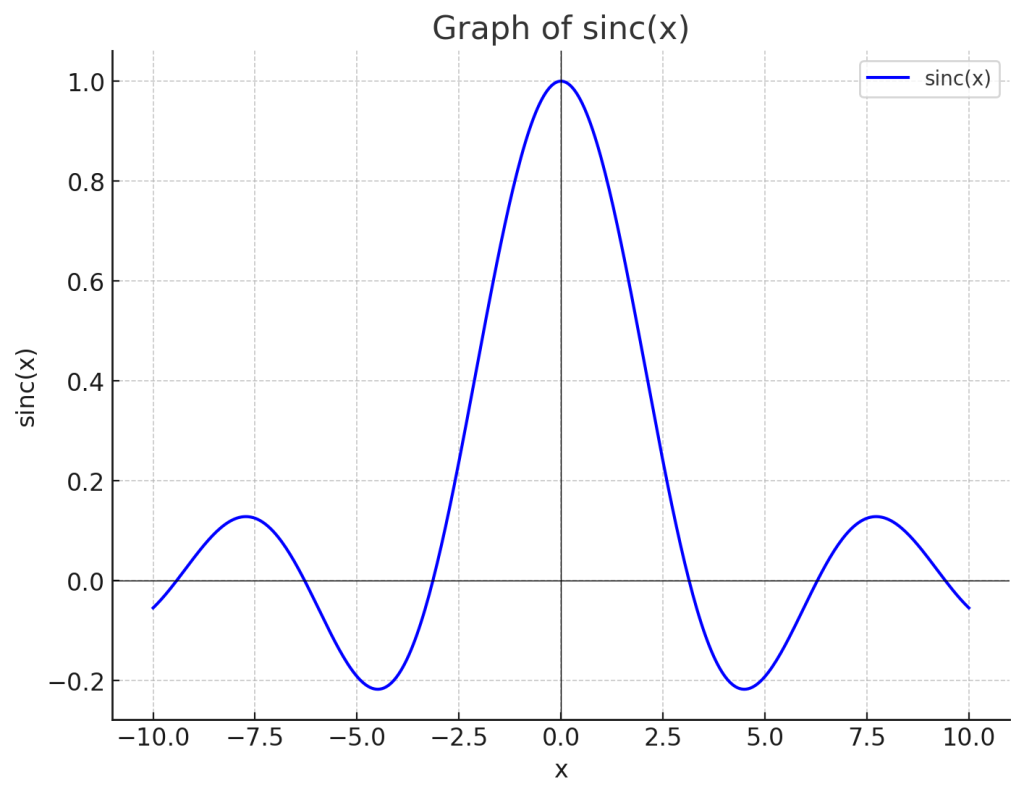
sinc関数のグラフは、減衰しながら振動する形状を持ちます。主要な特徴は以下の通りです。
- 最大値: \( x = 0 \) で \( \text{sinc}(0) = 1 \)。
- 零点: \( x = n\pi \)(\( n \) は 0 でない整数)の位置で零点を持ちます。
- 振幅の減衰: 振幅は \( x \) の増加に伴い、減衰します。
グラフを描くと、中央から左右に行くにつれて波形の高さが減少し、波長は一定のままになります。