四角数とは？性質と具体例について

$ふゅか$

ふゅか

四角数について知ってる？自然数を2乗した数なんだけど、例えば1, 4, 9, 16とかね。

$はるか$

はるか

うん、知ってるよ。$n$番目の四角数は$n^2$で表せる。

1. 四角数とは
2. 四角数の性質
2.1. シグマ
2.2. 四角数の漸化式

1. 四角数とは

n番目の四角数$T_n$は次のように表されます。

\[ T_n = n^2 \]

例えば、

$T_1= 1^2 = 1 $
$ T_2= 2^2 = 4 $
$T_3= 3^2 = 9 $
$T_4= 4^2 = 16 $
$ T_5= 5^2 = 25 $

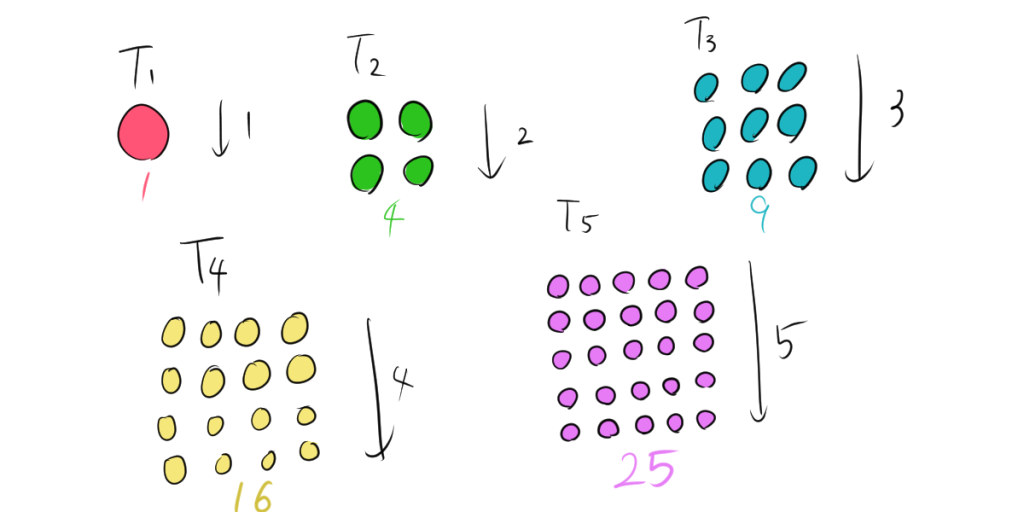
これらの数は、点を正方形のように配置すると、次のような四角の形に並べられます。

四角数（square numbers）とは、自然数を2乗した数のことです。50個の四角数を横に並べてみましょう。

\[ 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500 \]

2. 四角数の性質

$ふゅか$

ふゅか

じゃあ、四角数の性質についても見てみようか。

2.1. シグマ

$1$から$2n-1$までの和を計算すると

$$\sum^{n}_{k=1} 2k-1 = n^2$$

シグマの計算公式より

$$\begin{align*} \sum^{n}_{k=1} (2k-1) &= 2\sum^{n}_{k=1} k – \sum^{n}_{k=1} 1 \notag \\ &= 2\cdot\frac{n(n+1)}{2} – n \notag \\ &= n^2 + n – n \notag \\ &= n^2 \end{align*}$$

2.2. 四角数の漸化式

$n+1$番目と$n$番目の四角数は次のような漸化式で表すことができる。

$$T_{n+1} = T_{n}+2n+1$$

となる。

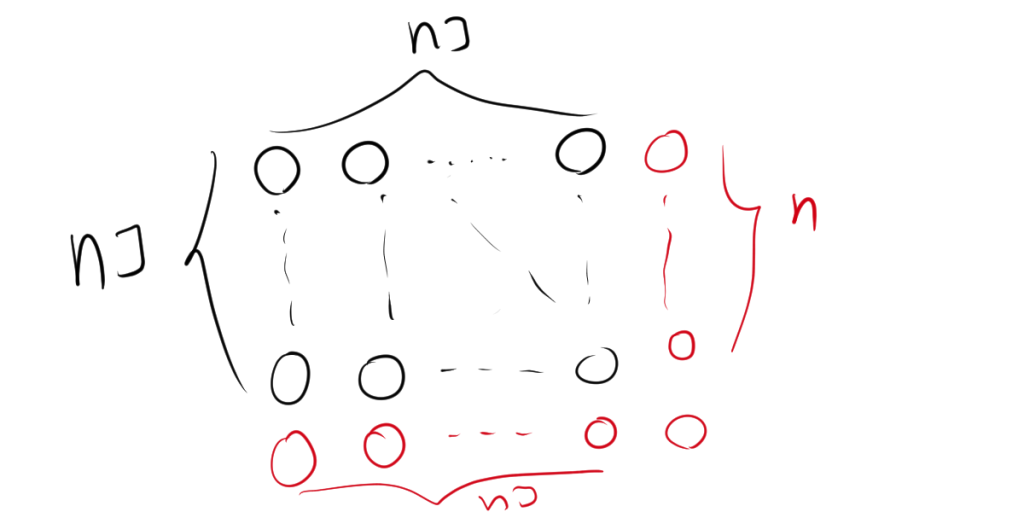
赤色の〇が$T_n$から$T_{n+1}$から増える個数である。

したがって、

$$T_{n+1} = T_{n}+n+n+1= T_{n}+2n+1$$

これは、階差数列にもなるので、$n\geq 2$のとき、

\[ \begin{align*} T_{n} &= T_1 + \sum_{k=1}^{n-1} (2k + 1) \\ &= 1 + 2\frac{n(n-1)}{2} + (n-1) \\ &= 1 + (n+1)(n-1) \\ &= 1 + n^2 – 1 \\ &= n^2 \end{align*} \]

また、$n=1$の時も成り立ちます。