部分空間の定義・具体例・性質・例題について

はるか

部分空間はベクトル空間の部分集合。

ふゅか

うん！その部分集合が条件を満たしている必要があるんだよ。具体的には加法とスカラー倍に対して閉じていること！

はるか

その2つの条件が大事。部分空間かどうかを確認する時は、その条件を確認する必要がある。

1. 部分空間とは

2. 部分空間の例

2.1. 例1：平面内の直線

加法に関して調べる。

直線 \( y = mx \) 上の任意の2つのベクトルを \(\mathbf{u} = (x_1, mx_1)\) と \(\mathbf{v} = (x_2, mx_2)\) とします。これらの和は \[ \mathbf{u} + \mathbf{v} = (x_1 + x_2, mx_1 + mx_2). \]

この和を \((x_3, y_3)\) とすると、\( x_3 = x_1 + x_2 \) および \( y_3 = mx_1 + mx_2 = m(x_1 + x_2) = mx_3 \) となります。したがって、\(\mathbf{u} + \mathbf{v}\) は直線 \( y = mx \) 上にあります。

次に、スカラー倍に関して調べる。

直線 \( y = mx \) 上の任意のベクトルを \(\mathbf{u} = (x_1, mx_1)\) とし、任意のスカラー \( c \) を取ります。このスカラー倍は \[ c\mathbf{u} = (cx_1, cmx_1). \]

これを \((x_2, y_2)\) とすると、\( x_2 = cx_1 \) および \( y_2 = cmx_1 = m(cx_1) = mx_2 \) となります。したがって、\( c\mathbf{u} \) も直線 \( y = mx \) 上にあります。

以上より、直線 \( y = mx \) は、加法とスカラー倍に関して閉じているので、\( \mathbb{R}^2 \) の部分空間であることが示されました。

はるか

直線 \( y = mx \) 上の任意の2つのベクトルを足しても、ちゃんと直線上にある。スカラー倍しても同じ。だから部分空間。

2.2. 例2：\( \mathbb{R}^3 \) の平面

加法に関して調べる。

平面 \( ax + by + cz = 0 \) 上の任意の2つのベクトルを \( \mathbf{u} = (x_1, y_1, z_1) \) と \( \mathbf{v} = (x_2, y_2, z_2) \) とします。これらのベクトルが平面上にあるということは、

\[ ax_1 + by_1 + cz_1 = 0 \]

および

\[ ax_2 + by_2 + cz_2 = 0 \]

が成り立ちます。

これらの和を考えます。

\[ \mathbf{u} + \mathbf{v} = (x_1 + x_2, y_1 + y_2, z_1 + z_2). \]

この和が平面上にあるかどうか調べるために、次の式を計算します。

\[ a(x_1 + x_2) + b(y_1 + y_2) + c(z_1 + z_2) \]

\[ =(ax_1 + by_1 + cz_1) + (ax_2 + by_2 + cz_2)\]

それぞれの項は、\( ax_1 + by_1 + cz_1 = 0 \) および \( ax_2 + by_2 + cz_2 = 0 \) なので、

\[ a(x_1 + x_2) + b(y_1 + y_2) + c(z_1 + z_2) ＝0\]

したがって、\( \mathbf{u} + \mathbf{v} \) も平面 \( ax + by + cz = 0 \) 上にあります。

スカラー倍に関して調べる。

平面 \( ax + by + cz = 0 \) 上の任意のベクトルを \( \mathbf{u} = (x_1, y_1, z_1) \) とし、任意のスカラー \( c \) を取ります。このベクトルは、

\[ ax_1 + by_1 + cz_1 = 0 \]

を満たします。

このベクトルのスカラー倍を考えます。

\[ c\mathbf{u} = (cx_1, cy_1, cz_1). \]

このベクトルが平面上にあるかどうか調べるために、次の式を計算します。 \[ a(cx_1) + b(cy_1) + c(cz_1). \]

これを展開すると、 \[ c(ax_1 + by_1 + cz_1). \]

もとのベクトル \( \mathbf{u} \) が平面上にあるので、 \[ ax_1 + by_1 + cz_1 = 0 \] が成り立ちます。よって、 \[ c \cdot 0 = 0. \]

したがって、\( c\mathbf{u} \) も平面 \( ax + by + cz = 0 \) 上にあります。

以上より、平面 \( ax + by + cz = 0 \) は、加法とスカラー倍に関して閉じているので、\( \mathbb{R}^3 \) の部分空間であることが示されました。

はるか

\( \mathbb{R}^3 \) の原点を通る平面も部分空間。\( ax + by + cz = 0 \) で表される平面。

ふゅか

そう！その平面上の2つのベクトルの和がまた平面上にあるし、スカラー倍も平面上に残るから、部分空間だといえるね。

3. 部分空間の性質

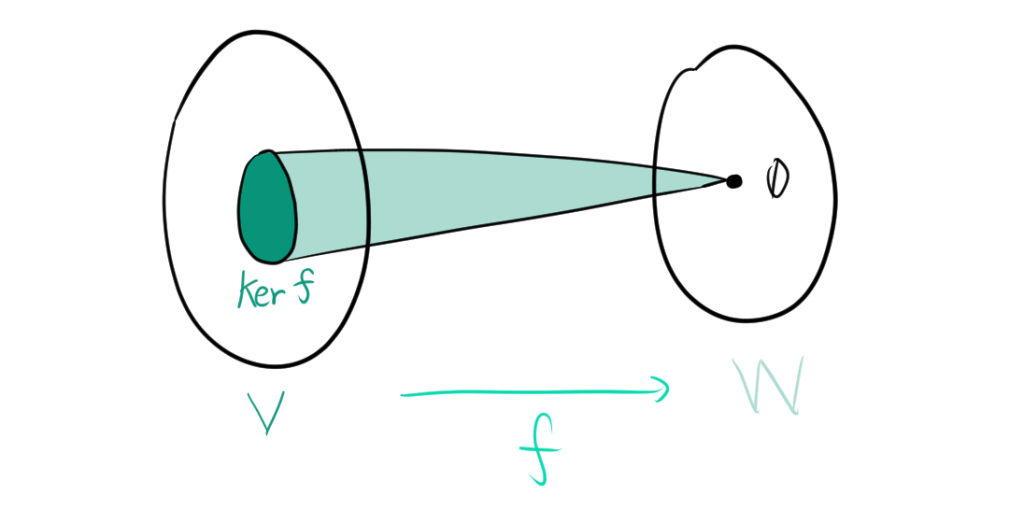
3.1. 線形写像の核と部分空間

ふゅか

線形写像の核も部分空間になるんだよ！それは、線形写像がゼロに写すベクトルの集合だから。

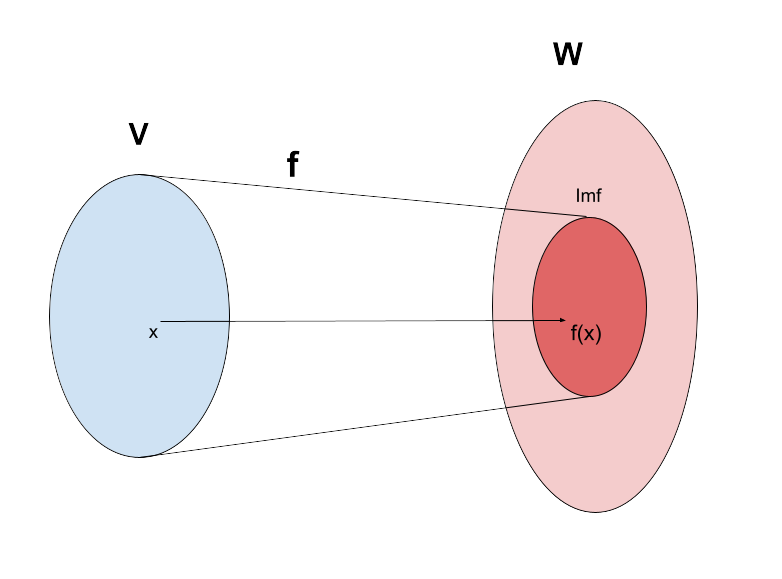
3.2. 線形写像の像と部分空間

はるか

あと、線形写像の像も部分空間。これは、\( f \) によって \( V \) のベクトルが写された集合が \( W \) の部分空間になるってこと。

4. 例題

4.1. 例題1

任意のベクトル \( (x_1, y_1, z_1) \) と \( (x_2, y_2, z_2) \) が \( W \) に含まれているとします。

\[ x_1 + y_1 + z_1 = 0 \quad \text{および} \quad x_2 + y_2 + z_2 = 0 \]

ベクトルの加法を考えます。

\[ (x_1, y_1, z_1) + (x_2, y_2, z_2) = (x_1 + x_2, y_1 + y_2, z_1 + z_2) \]

このベクトルが \( W \) に含まれるかどうか確認します。

\[ (x_1 + x_2) + (y_1 + y_2) + (z_1 + z_2) = (x_1 + y_1 + z_1) + (x_2 + y_2 + z_2) = 0 + 0 = 0 \]

よって、加法の閉性を満たします。

任意のベクトル \( (x, y, z) \in W \) とスカラー \( c \in \mathbb{R} \) を考えます。

\[ x + y + z = 0 \]

スカラー倍 \( c \) を考えます。

\[ c(x, y, z) = (cx, cy, cz) \]

このベクトルが \( W \) に含まれるかどうか確認します。

\[ cx + cy + cz = c(x + y + z) = c \cdot 0 = 0 \]

よって、スカラー倍の閉性を満たします。

したがって、集合 \( W \) は \( \mathbb{R}^3 \) の部分空間です。

4.2. 例題2

任意の \( (x_1, y_1), (x_2, y_2) \in V \) に対して、

\[ x_1y_1 = 0 \quad \text{および} \quad x_2y_2 = 0 \]

これらのベクトルの加法を考えます。

\[ (x_1, y_1) + (x_2, y_2) = (x_1 + x_2, y_1 + y_2) \]

このベクトルが \( V \) に含まれるか確認します。

\[ (x_1 + x_2)(y_1 + y_2) = x_1y_1 + x_1y_2 + x_2y_1 + x_2y_2 \]

\( x_1y_1 = 0 \) および \( x_2y_2 = 0 \) であっても、 \( x_1y_2 + x_2y_1 \) が必ず 0 になるとは限りません。

したがって、集合 \( V \) は \( \mathbb{R}^2 \) の部分空間ではありません。