シグマの計算公式の導出、計算方法について

はるか

シグマ計算ってさ、公式がいっぱいあるけど、最初に覚えるべきなのはどれ？

ふゅか

うーん、例えば、\(\displaystyle\sum_{k=1}^n k^2 \)、\(\displaystyle\sum_{k=1}^n k \)かな～。

1. シグマの計算

シグマ計算の代表的な公式を以下にまとめました。それぞれの公式を理解し、シグマ計算を効率よく進めるために役立ててください。

2. 各シグマ計算の公式の証明

2.1. 定数の和の公式

これは、定数 \( a \) を \( n \) 回足すことを意味します。

\[ a + a + \cdots + a \quad (\text{全部で } n \text{ 個}) \]

和は \( na \) となります。

2.2. 連続する自然数の和の公式

これは等差数列$a_n=a_{n-1}+1$の和であるので、等差数列の和の公式より、初項は1、末尾はnになるので、

$$\sum_{k=1}^{n} k=\frac{a_1+a_n}{2}n=\frac{(n+1)}{2}n$$

$\dfrac{(n+1)}{2}n$は三角数と呼ばれます。

2.3. 連続する自然数の二乗の和の公式

はるか

差分のシグマを使う。ちょっと難しいけど、計算の中で消える部分が出てくるから面白いかも。

差分のシグマの考え方を利用します。

$$\sum_{k=1}^n (k+1)^3-k^3$$

という差分が出てきて、えっ、3乗って思うかもしれませんが、$k^3$の部分が消えるので大丈夫です！計算すると、残りの項は$3k^2 + 3k + 1 $になって、 3k + 1 に関してはシグマの計算式がわかっているのでそれを利用します。

まず、次のような差分のシグマの式を計算すると

$$\begin{align*} \sum_{k=1}^n \left( (k+1)^3 – k^3 \right) &= \sum_{k=1}^n \left( 3k^2 + 3k + 1 \right) \\ &= \sum_{k=1}^n 3k^2 + \sum_{k=1}^n 3k + \sum_{k=1}^n 1 \\ &= 3\sum_{k=1}^n k^2 + \frac{3n^2 + 3n}{2} + n \\ &= 3\sum_{k=1}^n k^2 + \frac{3n^2 + 5n}{2} \end{align*}$$

一方で、$\sum_{k=1}^n f(k+1)-f(k) = f(n+1)-f(1)$であるので、

$$\begin{align*} \sum_{k=1}^n \left( (k+1)^3 – k^3 \right) &= (n+1)^3 – 1 \\ &= n^3 + 3n^2 + 3n \\ &= \frac{1}{2} (2n^3 + 6n^2 + 6n) \end{align*}$$

したがって、

$$\begin{align*} 3\sum_{k=1}^n k^2 + \frac{3n^2 + 5n}{2} &= \frac{1}{2} (2n^3 + 6n^2 + 6n) \\ 3\sum_{k=1}^n k^2 &= \frac{1}{2} (2n^3 + 3n^2 + n) \\ 3\sum_{k=1}^n k^2 &= \frac{1}{2} n (2n^2 + 3n + 1) \\ 3\sum_{k=1}^n k^2 &= \frac{1}{2} n (n+1) (2n+1) \\ \sum_{k=1}^n k^2 &= \frac{1}{6} n (n+1) (2n+1) \end{align*}$$

2.4. 連続する自然数の三乗の和の公式

はるか

確かに、二乗の和の証明とアプローチは同じだけど、計算が多い。

まず、次のような差分のシグマの式を考えます。

\[ \sum_{k=1}^n \left( (k+1)^4 – k^4 \right) \]

計算すると、

\[ \sum_{k=1}^n \left( (k+1)^4 – k^4 \right) = \sum_{k=1}^n (4k^3 + 6k^2 + 4k + 1) \]

これをさらに分解して、

\[ \sum_{k=1}^n 4k^3 + \sum_{k=1}^n 6k^2 + \sum_{k=1}^n 4k + \sum_{k=1}^n 1 \]

それぞれのシグマを計算します。

1. \(\sum_{k=1}^n 1 = n\)
2. \(\sum_{k=1}^n k = \frac{n(n+1)}{2}\)
3. \(\sum_{k=1}^n k^2 = \frac{1}{6} n (n+1) (2n+1)\)
4. \(\sum_{k=1}^n k^3 = ?\)（この部分を求めたい）

次に、差分のシグマの基本的な性質を利用します。

\[ \sum_{k=1}^n (f(k+1) – f(k)) = f(n+1) – f(1) \]

したがって、

\[ \sum_{k=1}^n \left( (k+1)^4 – k^4 \right) = (n+1)^4 – 1 \]

\[ = n^4 + 4n^3 + 6n^2 + 4n \]

これまでの計算結果を比較して、

\[ 4 \sum_{k=1}^n k^3 + 6 \sum_{k=1}^n k^2 + 4 \sum_{k=1}^n k + \sum_{k=1}^n 1 = n^4 + 4n^3 + 6n^2 + 4n \]

\[ 4 \sum_{k=1}^n k^3 + 6 \cdot \frac{1}{6} n (n+1) (2n+1) + 4 \cdot \frac{n(n+1)}{2} + n = n^4 + 4n^3 + 6n^2 + 4n \]

\[ 4 \sum_{k=1}^n k^3 + n(n+1)(2n+1) + 2n(n+1) + n = n^4 + 4n^3 + 6n^2 + 4n \]

\[ 4 \sum_{k=1}^n k^3 = n^4 + 4n^3 + 6n^2 + 4n – n(n+1)(2n+1) – 2n(n+1) – n \]

\[ 4 \sum_{k=1}^n k^3 = n^4 + 4n^3 + 6n^2 + 3n – n(n+1)(2n+1) – 2n(n+1)  \]

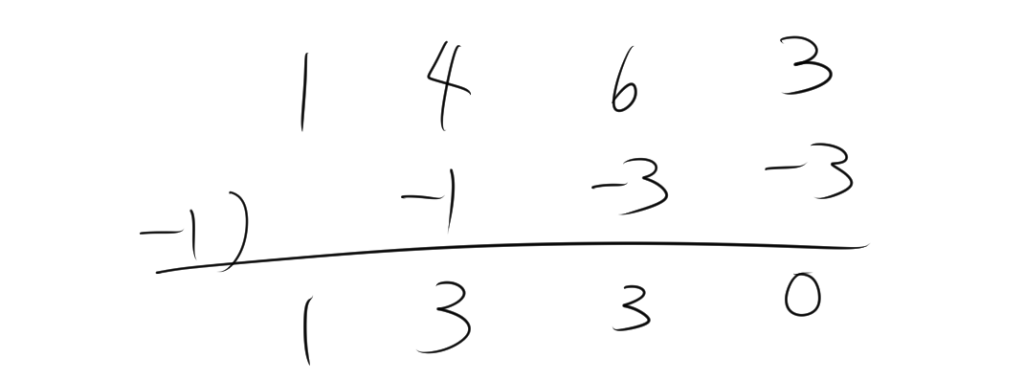
ここで、 $n(n^3+4n^2+6n+3)$を組立除法を利用して、因数分解すると、

したがって、

$$\begin{align*} 4 \sum_{k=1}^n k^3 &= n(n+1)(n^2+3n+3) – n(n+1)(2n+1) – 2n(n+1) \\ 4 \sum_{k=1}^n k^3 &= n(n+1)\{(n^2+3n+3) – 2n – 1 – 2\} \\ 4 \sum_{k=1}^n k^3 &= n(n+1)(n^2+n) \\ 4 \sum_{k=1}^n k^3 &= n^2(n+1)^2 \\ \sum_{k=1}^n k^3 &= \frac{n^2(n+1)^2}{4} \\ \sum_{k=1}^n k^3 &= \left(\frac{n(n+1)}{2}\right)^2 \end{align*}$$

2.5. 等比数列の和

証明は等比数列の和の公式を参考にしてください。

3. 例題

ふゅか

シグマの計算をしてみよう！

3.1. 例題 1

このシグマは、次のように分解できます。

\[ \sum_{i=1}^{5} (2i + 3) = \sum_{i=1}^{5} 2i + \sum_{i=1}^{5} 3 \]

まず、\(\displaystyle\sum_{i=1}^{5} 2i\)を計算します。

\[ \sum_{i=1}^{5} 2i = 2 \sum_{i=1}^{5} i = 2 \times \frac{1}{2} \times 5 \times (5 + 1) = 2 \times 15 = 30 \]

次に、\(\displaystyle\sum_{i=1}^{5} 3\)を計算します。

\[ \sum_{i=1}^{5} 3 = 5 \times 3 = 15 \]

したがって、

\[ \sum_{i=1}^{5} (2i + 3) = 30 + 15 = 45 \]

3.2. 例題 2

\(n = 10\)なので、

\[ \sum_{k=1}^{10} k^2 = \frac{1}{6} \times 10 \times (10 + 1) \times (2 \times 10 + 1) = \frac{1}{6} \times 10 \times 11 \times 21 \]

計算すると、

\[ \frac{1}{6} \times 10 \times 11 \times 21 = 385 \]

したがって、

\[ \sum_{k=1}^{10} k^2 = 385 \]

3.3. 例題 3

\[ \sum_{n=0}^{4} 3^n = 1 \cdot \frac{1 – 3^{4+1}}{1 – 3} = \frac{1 – 3^5}{-2} = \frac{1 – 243}{-2} = \frac{-242}{-2} = 121 \]

したがって、

\[ \sum_{n=0}^{4} 3^n = 121 \]

3.4. 例題 4

このシグマも分けて考えます。

\[ \sum_{m=1}^{6} (m^2 – m) = \sum_{m=1}^{6} m^2 – \sum_{m=1}^{6} m \]

まず、\(\displaystyle\sum_{m=1}^{6} m^2\)を計算します。

\[ \sum_{m=1}^{6} m^2 = \frac{1}{6} \times 6 \times (6 + 1) \times (2 \times 6 + 1) = \frac{1}{6} \times 6 \times 7 \times 13 = 91 \]

次に、\(\displaystyle\sum_{m=1}^{6} m\)を計算します。

\[ \sum_{m=1}^{6} m = \frac{1}{2} \times 6 \times (6 + 1) = 21 \]

したがって、

\[ \sum_{m=1}^{6} (m^2 – m) = 91 – 21 =70 \]

3.5. 例題 5

\[ \sum_{j=1}^{8} (j + 2)^2 = \sum_{j=1}^{8} (j^2 + 4j + 4) = \sum_{j=1}^{8} j^2 + \sum_{j=1}^{8} 4j + \sum_{j=1}^{8} 4 \]

まず、\(\displaystyle\sum_{j=1}^{8} j^2\)を計算します。 \[ \sum_{j=1}^{8} j^2 = \frac{1}{6} \times 8 \times (8 + 1) \times (2 \times 8 + 1) = \frac{1}{6} \times 8 \times 9 \times 17 = 204 \]

次に、\(\displaystyle\sum_{j=1}^{8} 4j\)を計算します。 \[ \sum_{j=1}^{8} 4j = 4 \sum_{j=1}^{8} j = 4 \times \frac{1}{2} \times 8 \times (8 + 1) = 4 \times 36 = 144 \]

最後に、\(\displaystyle\sum_{j=1}^{8} 4\)を計算します。 \[ \sum_{j=1}^{8} 4 = 8 \times 4 = 32 \]

したがって、 \[ \sum_{j=1}^{8} (j + 2)^2 = 204 + 144 + 32 = 380 \]