上限 (sup) と下限 (inf) の意味・定義・具体例・例題について

1. 上限 (sup, supremum)について
1.1. 上限の意味・定義
1.2. 上限の具体例
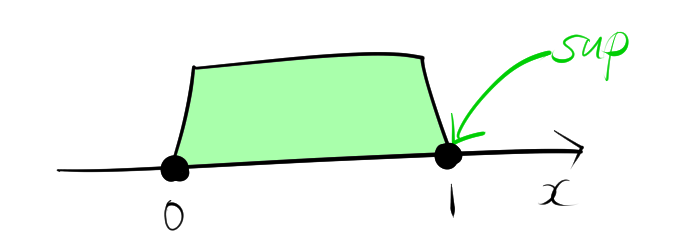
集合 \( S = \{ x \in \mathbb{R} \mid 0 \leq x < 1 \} \) の上限は 1 です。これは、1 が集合 \( S \) の要素のすべてを覆う最小の上界であるためです。ただし、1 は \( S \) の要素ではありません。
2. 下限 (inf, infimum)について
2.1. 下限の定義
2.2. 下限の具体例
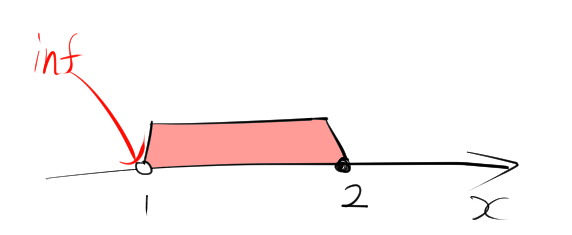
集合 \( T = \{ x \in \mathbb{R} \mid 1 < x \leq 2 \} \) の下限は 1 です。これは、1 が集合 \( T \) の要素のすべてを覆う最大の下界であるためです。ただし、1 は \( T \) の要素ではありません。
3. 例題
3.1. 例題 1: 有限集合の場合
- 最大値 (max): \( S \) の最大の要素は \( 5 \) です。したがって、最大値は \( \max S = 5 \) です。
- 最小値 (min): \( S \) の最小の要素は \( 1 \) です。したがって、最小値は \( \min S = 1 \) です。
- 上限 (sup): この場合、上限は最大値と同じであり、\( \sup S = 5 \) です。
- 下限 (inf): この場合、下限は最小値と同じであり、\( \inf S = 1 \) です。
3.2. 例題 2: 0 < x < 1
- 最大値 (max): \( T \) には最大値は存在しません。1 に限りなく近づく要素はあっても、1 そのものは \( T \) に含まれていません。
- 最小値 (min): \( T \) には最小値も存在しません。0 に限りなく近づく要素はあっても、0 そのものは \( T \) に含まれていません。
- 上限 (sup): この場合、上限は \( 1 \) です。つまり、\( \sup T = 1 \) です。これは、1 より大きい \( T \) の上界は存在せず、1 は最小の上界だからです。
- 下限 (inf): この場合、下限は \( 0 \) です。つまり、\( \inf T = 0 \) です。これは、0 より小さい \( T \) の下界は存在せず、0 は最大の下界だからです。
3.3. 例題 3: 数列の上限と下限
まず、最大値について考えます。
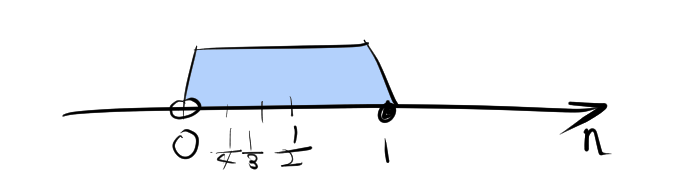
数列 \( S \) の最初の項は \( a_1 = \frac{1}{1} = 1 \) です。数列の各項 \( a_n = \frac{1}{n} \) は \( n \) が増加するにつれて減少する単調減少な数列です。したがって、数列の最大値は最初の項であり、\( \max S = 1 \) です。
次に、最小値について考えます。
数列 \( a_n = \frac{1}{n} \) は \( n \) が増加するにつれて 0 に限りなく近づき単調減少します。よって、\( S \) には最小値は存在しません。
次に、上限 (sup)について考えます。
上限は集合の最小の上界です。数列 \( S \) の各項は 1 より小さいですが、1 が最小の上界であるため、上限は \( \sup S = 1 \) です。
最後に、下限 (inf)について考えます。
下限は集合の最大の下界です。数列の各項 \( a_n \) は 0 に限りなく近づきますが、どの項も 0 より大きいです。よって、数列の下限は 0 です。つまり、\( \inf S = 0 \) です。
以上の結果をまとめると、次のようになります。
- 最大値 \( \max S = 1 \)
- 最小値:存在しない
- 上限 \( \sup S = 1 \)
- 下限 \( \inf S = 0 \)