【写像】全射・単射・全単射の意味、具体例について

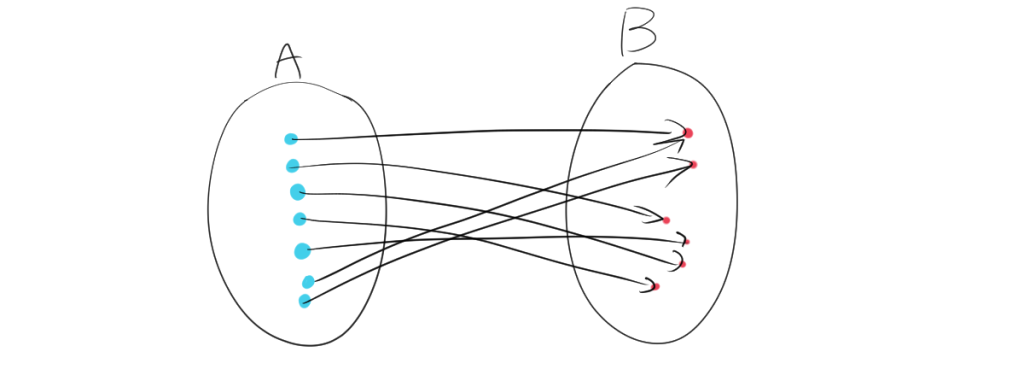
1. 全射(Surjection)
全射とは、写像 \( f: A \to B \) において、集合 \( B \) のすべての要素が \( A \) の何らかの要素に対応するものです。つまり、集合 \( B \) のどの要素も、少なくとも1つの \( A \) の要素に対応しています。
1.1. 例
集合 \( A = \{1, 2, 3\} \)、集合 \( B = \{a, b\} \) に対して、写像 \( f \) を以下のように定義します。
- \( f(1) = a \)
- \( f(2) = a \)
- \( f(3) = b \)
この場合、集合 \( B \) のすべての要素が集合 \( A \) から写像されているため、\( f \) は全射です。
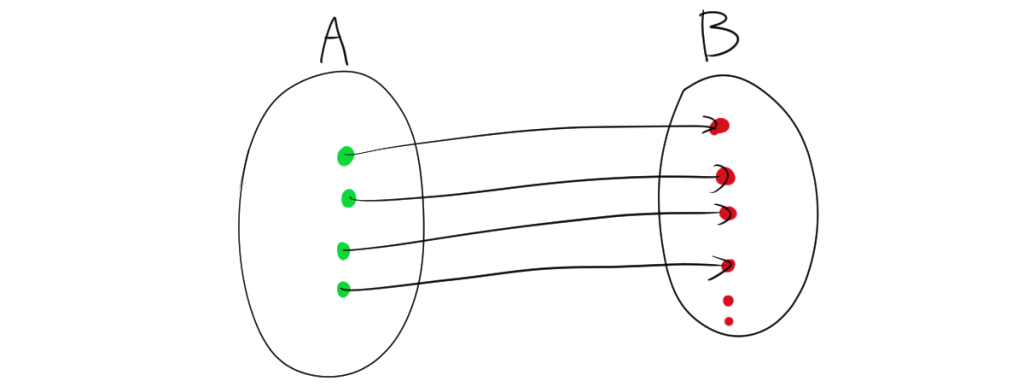
2. 単射(Injection)
単射とは、写像 \( f: A \to B \) において、異なる \( A \) の要素が異なる \( B \) の要素に写されるものです。つまり、異なる入力は異なる出力に対応します。
2.1. 例
集合 \( A = \{1, 2, 3\} \)、集合 \( B = \{a, b, c,d\} \) に対して、写像 \( f \) を以下のように定義します。
- \( f(1) = a \)
- \( f(2) = b \)
- \( f(3) = c \)
この場合、異なる要素が異なる値に写されているので、\( f \) は単射です。
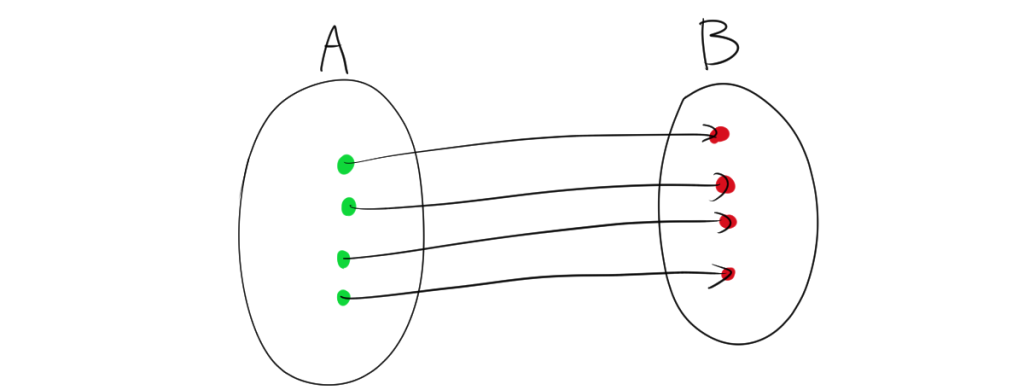
3. 全単射(Bijection)
全単射とは、全射と単射の両方の性質を持つ写像です。つまり、全単射は、集合 \( A \) のすべての要素が集合 \( B \) の異なる要素に一意に対応し、かつ集合 \( B \) のすべての要素に対応する写像です。
3.1. 例
集合 \( A = \{1, 2, 3\} \)、集合 \( B = \{a, b, c\} \) に対して、写像 \( f \) を以下のように定義します:
- \( f(1) = a \)
- \( f(2) = b \)
- \( f(3) = c \)
この場合、\( A \) のすべての要素が \( B \) の一意な要素に対応し、かつ \( B \) のすべての要素が \( A \) から写像されているため、\( f \) は全単射です。
4. 具体例
4.1. 例1: 全射の例
関数 \( f: \mathbb{Z} \to \mathbb{Z} \), \( f(x) = x \pmod 2 \)
- 定義域: \(\mathbb{Z}\)(全ての整数)
- 終域: \(\mathbb{Z}_2 = \{0, 1\}\)(整数を2で割ったあまり)
この場合、によって、任意の整数 \( x \) は 0 または 1 に対応します。終域の全ての要素(0, 1)に対応するため、全射です。しかし、異なる \( x \) が同じ \( y \) に対応することがあるため、単射ではありません。
4.2. 例2: 全単射の例
関数 \( f: \mathbb{R} \to \mathbb{R} \), \( y = x \).
- 定義域: \(\mathbb{R}\)
- 終域: \(\mathbb{R}\)
この場合、定義域と終域が同じで、全ての整数 \( x \) が異なる \( y \) に対応し、かつすべての \( y \) に対応する \( x \) が存在します。したがって、全単射です。
5. まとめ
- 全射: すべての出力がカバーされている(\( f(A) = B \))。
- 単射: 入力が一意に決まる(異なる入力は異なる出力)。
- 全単射: 全射であり、かつ単射(1対1対応)。