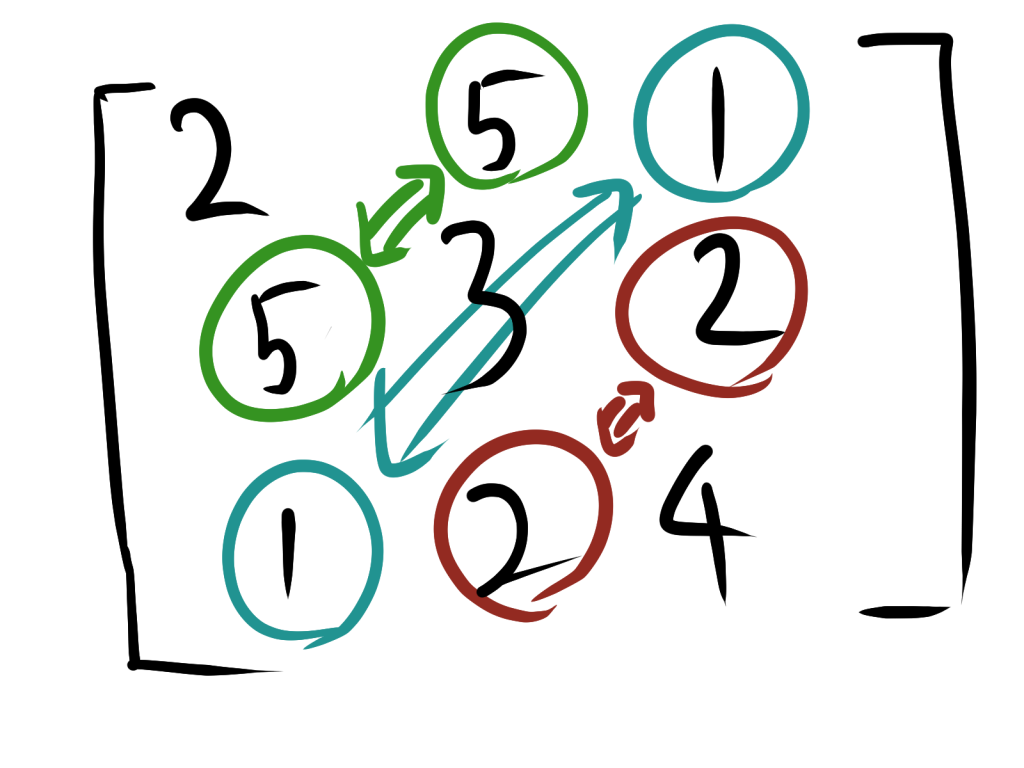実対称行列の定義・具体例・性質・例題について

1. 実対称行列

つまり、行列の要素について、$a_{ij}=a_{ji}$が成り立っています。

1.1. 対称行列の具体例

$\begin{bmatrix} 1 & 2 \\ 2 & 3 \\ \end{bmatrix}$

$\begin{bmatrix} 2 & 5 & 1 \\ 5 & 3 & 2 \\ 1 & 2 & 4 \\ \end{bmatrix}$

2. 対称行列の性質

2.1. $AA^T$の行列の積は対称行列になる

行列の積の転置をとると、

$(AA^T)^T$

$=(A^T)^TA^T$

$=AA^T$

したがって、$(AA^T)^T=AA^T$となるため、対称行列である。

2.2. $A+A^T$は対称行列になる

Aは正方行列とする。$A+A^T$を転置すると、

$(A+A^T)^T$

$=A^T+(A^T)^T$

$=A+A^T$

となる。

したがって、$(A+A^T)^T=A+A^T$となるため、$A+A^T$は対称行列となる。

 

2.3. 固有値は実数になる

対称行列$A$の固有値を$\lambda$とすると、$\lambda=\overline{\lambda}$を示すことができればよい。

固有値の定義より、

$Ax=\lambda x$

となる。複素共役を取ると、

$A\overline{x}=\overline\lambda \overline x$

[1]まず、$A\overline{x}=\overline\lambda \overline x$を変形します。

転置を行うと、

$(A\overline{x})^T=\overline\lambda \overline x^T$

$\overline{x}^TA^T=\overline\lambda \overline x^T$

$A$は対称行列であるから、$A^T=A$より、

$\overline{x}^TA^T=\overline{x}^TA$

$=\overline\lambda \overline x^T$

右から$x$をかけると、

$\overline{x}^TAx=\overline\lambda \overline x^Tx$

$=\overline\lambda\|x\|^2$

[2]次に、$Ax=\lambda x$を変形します。

左から$\overline{x}^T$をかけると、

$\overline{x}^TAx=\lambda\overline{x}^T x$

$=\lambda\|x\|^2$

[1]と[2]より、式変形した式を引くと、

$\lambda\|x\|^2-\overline\lambda\|x\|^2=0$

$\therefore(\lambda-\overline\lambda)\|x\|^2=0$

固有ベクトルは0ベクトルではないため、

$\lambda=\overline\lambda$

となる。

2.4. 異なる固有ベクトルは直行する

前提として、異なる固有値が存在するとします。

対称行列Aの異なる固有値を$\lambda_1,\lambda_2$とします。固有値の定義より、

$Ax_1=\lambda_1 x_1$

$Ax_2=\lambda_2 x_2$

となる。それぞれの式を変形する。

$Ax_1=\lambda_1 x_1$を式変形する。

$(Ax_1)^T=\lambda_1 x_1^T$

$x_1^TA^T=\lambda_1 x_1^T$

対称行列は$A=A^T$となるから、

$x_1^TA=\lambda_1 x_1^T$

右から$x_2$をかけると

$x_1^TAx_2=\lambda_1 x_1^Tx_2$

となる。

次に$Ax_2=\lambda_2 x_2$を式変形する。

右から$x_1^T$をかけると、

$x_1^TAx_2=\lambda_2 x_1^Tx_2$

となる。

よって、式変形した式をともに引くと、

$\lambda_1 x_1^Tx_2-\lambda_2 x_1^Tx_2=0$

$(\lambda_1-\lambda_2) x_1^Tx_2=0$

となる。$\lambda_1-\lambda_2$は異なる固有値であるから、$x_1^Tx_2=0$となる。

$x_1$と$x_2$は0ベクトルではないから、内積が0ということになるため、固有ベクトル$x_1$と$x_2$は直行する。

2.5. 対称行列と交代行列の性質

正方行列は対称行列と交代行列の和で表すことができます。

$A$を正方行列とする。

$A=\dfrac{1}{2}A+\dfrac{1}{2}A$

$=\dfrac{1}{2}A+\dfrac{1}{2}A+\dfrac{1}{2}A^T-\dfrac{1}{2}A^T$

$=\dfrac{1}{2}(A+A^T)+\dfrac{1}{2}(A-A^T)$

$A+A^T$は対称行列、$A-A^T$は交代行列であるから、正方行列は対称行列と交代行列の和で表すことができるということが分かった。

3. 対称行列の例題

3.1. 例題1（$AA^T$）

まず、行列 \( A \) の転置行列 \( A^T \) を求めます。

\[ A^T = \begin{pmatrix} a & d \\ b & e \\ c & f \end{pmatrix} \]

次に、行列積 \( AA^T \) を計算します。

\[ AA^T = \begin{pmatrix} a & b & c \\ d & e & f \end{pmatrix} \begin{pmatrix} a & d \\ b & e \\ c & f \end{pmatrix} \]

\[ = \begin{pmatrix} a^2 + b^2 + c^2 & ad + be + cf \\ ad + be + cf & d^2 + e^2 + f^2 \end{pmatrix} \]

です。この行列は、上三角成分と下三角成分が等しいため、対称行列です。

したがって、行列積 \( AA^T \) は対称行列になります。

3.2. 例題2 （$A+A^T$）

$A+A^T$

$=\begin{bmatrix} 1 & 2 \\ 0 & 3 \\ \end{bmatrix}+\begin{bmatrix} 1 & 0 \\ 2 & 3 \\ \end{bmatrix}$

$=\begin{bmatrix} 2 & 2 \\ 2 & 6 \\ \end{bmatrix}$

となる。

$\begin{bmatrix} 2 & 2 \\ 2 & 6 \\ \end{bmatrix}$は対称行列になっているため、$A+A^T$が対称行列になっていることを確認することができた。

3.3. 例題３（固有値が実数であることを確認）

$\mathrm{det}(A-\lambda E)=0$を満たす$\lambda$を求めると、

$\begin{vmatrix} 1-\lambda & 2 \\ 2 & 1-\lambda \\ \end{vmatrix}$

$=(1-\lambda)(1-\lambda)-4$

$=\lambda^2-2\lambda-3$

$\therefore (\lambda-3)(\lambda+1)=0$

したがって、固有値は$\lambda=-1,3$となる。

3.4. 例題4（固有ベクトルが直交する）

先ほど、固有値は$\lambda=-1,3$であると計算した。固有ベクトルを求める。

[1]$\lambda=-1$のとき

固有ベクトルを$\begin{bmatrix}x\\y \end{bmatrix}$とする。

$\begin{bmatrix} 2 & 2\\ 2 &2 \\ \end{bmatrix}\begin{bmatrix}x\\y \end{bmatrix}=\boldsymbol{0}$

連立方程式の係数行列の階数を求めると、$\mathrm{rank}\begin{bmatrix} 2 & 2\\ 2 &2 \\ \end{bmatrix}=1$となるため、解の自由度は1である。したがって、$s\neq0$を満たす実数を用いて、$x=s$と置くと、$y=-s$となる。よって、固有ベクトルは、

$\begin{bmatrix}x\\y \end{bmatrix}=s\begin{bmatrix}1\\-1 \end{bmatrix}$

[2]$\lambda=-1$のとき

固有ベクトルを$\begin{bmatrix}x\\y \end{bmatrix}$とする。

$\begin{bmatrix} -2 & 2\\ 2 &-2 \\ \end{bmatrix}\begin{bmatrix}x\\y \end{bmatrix}=\boldsymbol{0}$

連立方程式の係数行列の階数を求めると、$\mathrm{rank}\begin{bmatrix} -2 & 2\\ 2 &-2 \\ \end{bmatrix}=1$となるため、解の自由度は1である。したがって、$s\neq0$を満たす実数を用いて、$x=s$と置くと、$y=s$となる。よって、固有ベクトルは、

$\begin{bmatrix}x\\y \end{bmatrix}=s\begin{bmatrix}1\\1 \end{bmatrix}$

となる。

[1][2]より、固有ベクトルは$\begin{bmatrix}1\\1 \end{bmatrix}$、$\begin{bmatrix}1\\-1 \end{bmatrix}$となり、内積が0となるため、直行していることがわかる。

3.5. 例題5（対称行列と交代行列の和）

行列 \( A \) を対称行列と交代行列の和として表現します。

1. 対称行列 \( B \) は、行列 \( A \) の転置行列との和の半分として得られます。
\[ B = \frac{1}{2}(A + A^T) = \frac{1}{2} \left(\begin{pmatrix} 2 & 3 \\ 5 & 4 \end{pmatrix} + \begin{pmatrix} 2 & 5 \\ 3 & 4 \end{pmatrix}\right) = \frac{1}{2} \begin{pmatrix} 4 & 8 \\ 8 & 8 \end{pmatrix} = \begin{pmatrix} 2 & 4 \\ 4 & 4 \end{pmatrix} \]

2. 交代行列 \( C\) は、行列 \( A \) とその転置行列との差の半分として得られます。
\[ C = \frac{1}{2}(A – A^T) = \frac{1}{2} \left(\begin{pmatrix} 2 & 3 \\ 5 & 4 \end{pmatrix} – \begin{pmatrix} 2 & 5 \\ 3 & 4 \end{pmatrix}\right) = \frac{1}{2} \begin{pmatrix} 0 & -2 \\ 2 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \]

\[B+C = \begin{pmatrix} 2 & 4 \\ 4 & 4 \end{pmatrix} + \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} 2 & 3 \\ 5 & 4 \end{pmatrix}\]これは元の行列 \( A \) と一致することが確認できます。