【Python・SymPy】固有値と固有ベクトルを求める方法のeigenvals()の使い方について

はるか

固有値と固有ベクトルの計算って、大変。

ふゅか

SymPyを使えば、びっくりするくらい簡単だよ！

はるか

やり方を教えて。

1. SymPyと固有値と固有ベクトル

固有値と固有ベクトルは線形代数において重要な概念です。Pythonの数式処理ライブラリである SymPy を使えば、これらを簡単に計算することができます。この記事では、SymPyを使って固有値と固有ベクトルを求める方法をわかりやすく解説します。

1.1. 固有値と固有ベクトルとは？

2. Sympyを利用した固有値と固有ベクトルの計算

以下の例を通して、具体的な手順を見ていきましょう。

2.1. 必要なモジュールのインポート

まずはSymPyをインポートし、行列を定義します。

from sympy import Matrix, symbols

# 行列を定義
A = Matrix([
    [4, 2],
    [1, 3]
])

上記のコードでは、2×2行列 \( A \) を定義しています。

2.2. 固有値の計算

固有値は、eigenvals() で計算できます。

# 固有値を求める
eigenvalues = A.eigenvals()
print("固有値:", eigenvalues)

実行結果は次のようになります。

固有値: {5: 1, 2: 1}

ここで、キーが固有値、値がその重複度です。

はるか

固有値はどうやって求めるの？

ふゅか

SymPyの eigenvals() を使えば一発！結果が辞書形式で返ってくるの。キーが固有値、値が重複度！

2.3. 固有ベクトルの計算

固有ベクトルは、eigenvects() メソッドで計算できます。

from IPython.display import display, Math
from sympy import latex
# 固有ベクトルを求める
eigenvectors = A.eigenvects()
for val, mult, vecs in eigenvectors:
    # 固有値をLaTeX形式で表示
    display(Math(r"\text{固有値: }" + latex(val)))
    # 固有ベクトルをLaTeX形式で表示
    for vec in vecs:
        display(Math(r"\text{固有ベクトル: }" + latex(vec)))

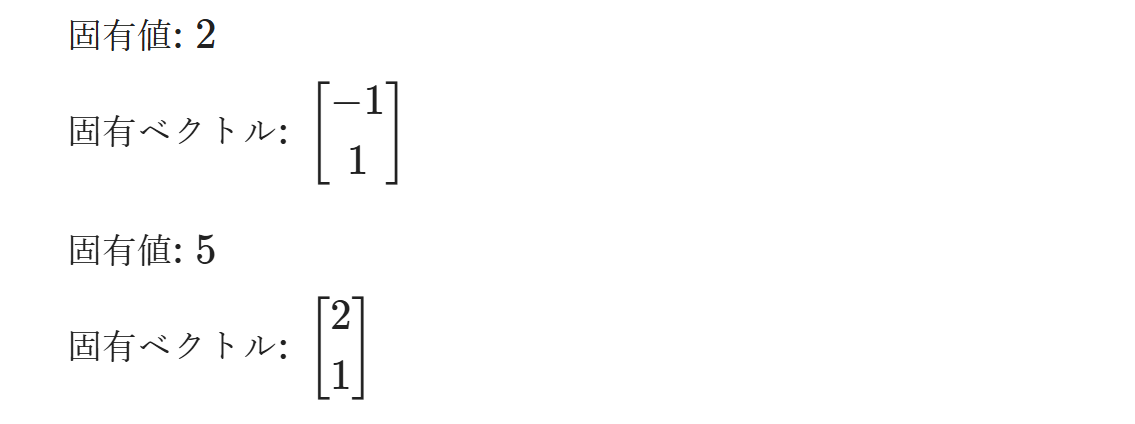
結果は次のようになります。

この出力は、行列 \( A \) に固有値 5 が対応する固有ベクトル \( [2, 1]^T \) を持ち、固有値 2 が対応する固有ベクトル \( [-1, 1]^T \) を持つことを示しています。また数式の表示には、jupyter labで数式を表示する方法で紹介したように、displayを使います。

はるか

固有ベクトルは？

ふゅか

eigenvects() を使うだけ！固有値ごとに対応するベクトルが簡単に取り出せるよ！

3. シンボルを利用

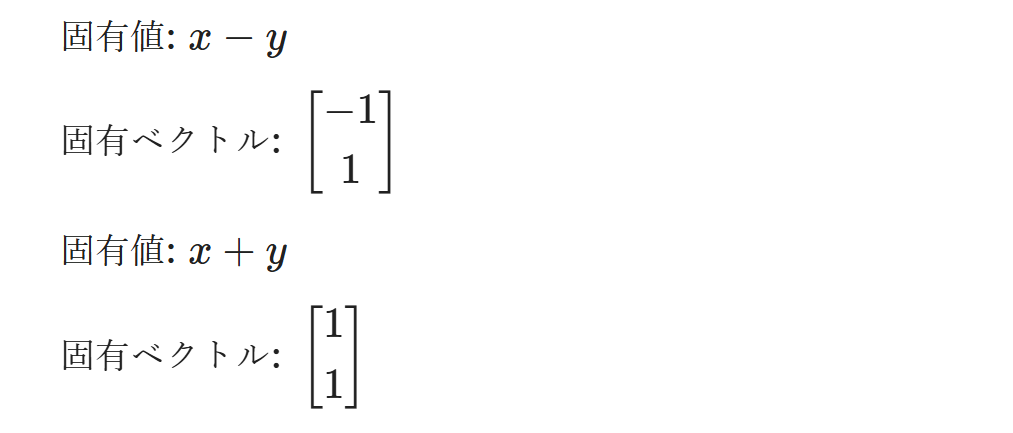
SymPyの利点は、シンボル（記号）を扱えることです。記号を用いて計算を一般化することも可能です。例えば、

$$\begin{bmatrix} x & y \\ y & x\end{bmatrix}$$

の行列の固有値・固有ベクトルを計算してみます。

from sympy import symbols
from IPython.display import display, Math
from sympy import latex
# 記号を用いた行列の定義
x, y = symbols('x y')
B = Matrix([
    [x, y],
    [y, x]
])

# 固有値・固有ベクトルを求める
eigenvectors = B.eigenvects()

for val, mult, vecs in eigenvectors:
    # 固有値をLaTeX形式で表示
    display(Math(r"\text{固有値: }" + latex(val)))
    # 固有ベクトルをLaTeX形式で表示
    for vec in vecs:
        display(Math(r"\text{固有ベクトル: }" + latex(vec)))