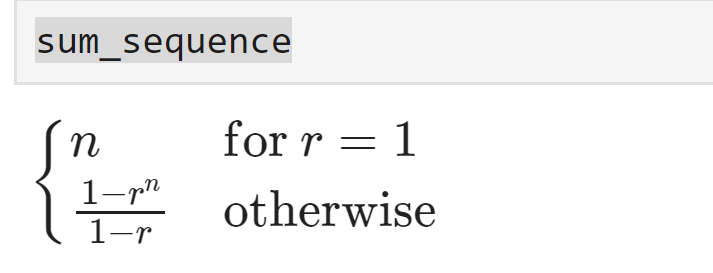SymPyで学ぶ！Pythonで漸化式の和を計算する方法

1. 数列の和の計算

SymPyを使用して数列の和を計算することができます。数列の和を計算するには、summationメソッドを使用します。以下に、SymPyを使用して数列の和を計算する基本的な方法を示します。

2. 基本的な使用例

まず、SymPyを使用して等差数列の和を計算する例を示します。

2.1. 等差数列の和

例えば、数列 \( 1, 2, 3, \ldots, n \) の和を計算します。

\[ 1 +2 + 3 +4  \cdots + n = \sum_{k=1}^{n} k = \dfrac{n(n-1)}{2} \]

import sympy as sp

# 変数の定義
n = sp.symbols('n')
i = sp.symbols('i', integer=True)

# 等差数列の定義
sequence = i

# 数列の和の計算
sum_sequence = sp.summation(sequence, (i, 1, n))

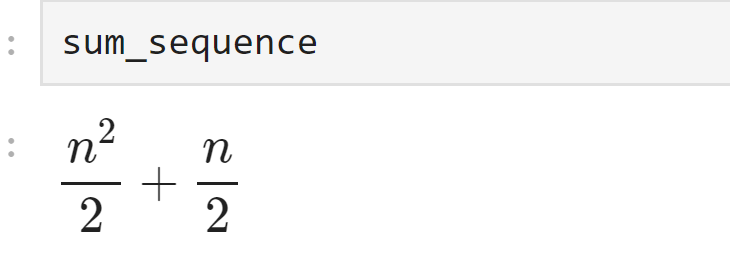
print("数列の和:", sum_sequence)

出力は次のようになります。

2.2. 等比数列の和

次に、等比数列の和を計算する例を示します。例えば、数列 \( 1, r, r^2, \ldots, r^{n-1} \) の和を計算します。

\[ 1 +r + r^2 +r^3 \cdots +r^{n-1} = \sum_{k=0}^{n-1} r^k= \dfrac{r^{n-1}-1}{r-1} \]

# 変数の定義
r = sp.symbols('r')

# 等比数列の定義
sequence = r**i

# 数列の和の計算
sum_sequence = sp.summation(sequence, (i, 0, n-1))

print("数列の和:", sum_sequence)

このコードは、等比数列 \( 1 + r + r^2 + \ldots + r^{n-1} \) の和を計算し、結果を表示します。出力は次のようになります。

2.3. シンボリックな数列の和

SymPyを使用してシンボリックな数列の和を計算することもできます。

例えば、数列 \( a_1, a_2, a_3, \ldots, a_n \) の和を計算します。

\[ a_1+a_2+a_3 + a_4 + \cdots +a_n= \sum_{k=1}^{n} a_k \]

# シンボリック変数の定義
a = sp.Function('a')

# シンボリックな数列の定義
sequence = a(i)

# 数列の和の計算
sum_sequence = sp.summation(sequence, (i, 1, n))

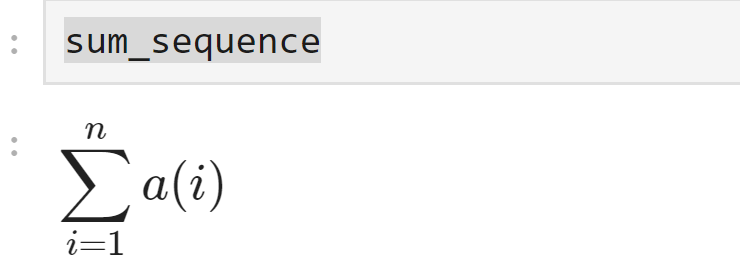
print("シンボリックな数列の和:", sum_sequence)

このコードは、シンボリックな数列 \( a_1 + a_2 + a_3 + \ldots + a_n \) の和を計算し、結果を表示します。出力は次のようになります。

2.4. 無限数列の和

SymPyを使用して無限数列の和（無限級数）を計算することもできます。以下にその例を示します。

例えば、数列 \( \frac{1}{2^i} \) の無限和を計算します。

\[ \frac{1}{2^0} + \frac{1}{2^1} + \frac{1}{2^2}  \cdots = \sum_{k=0}^{\infty} \left (\dfrac{1}{2} \right)^k= 2 \]

i=sp.symbols("i")
# 無限数列の定義
sequence = 1/2**i

# 数列の無限和の計算
sum_sequence = sp.summation(sequence, (i, 0, sp.oo))

print("無限数列の和:", sum_sequence)

このコードは、無限数列 \( \frac{1}{2^0} + \frac{1}{2^1} + \frac{1}{2^2} + \ldots \) の和を計算し、結果を表示します。出力は次のようになります。

2.5. バーゼル問題

バーゼル問題\[ \sum_{n=1}^{\infty} \frac{1}{n^2} = 1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \cdots = \frac{\pi^2}{6} \]を計算します。

i=sp.symbols("i")

# 数列の定義
sequence = 1/i**2

# 数列の無限和の計算
sum_sequence = sp.summation(sequence, (i, 1, sp.oo))

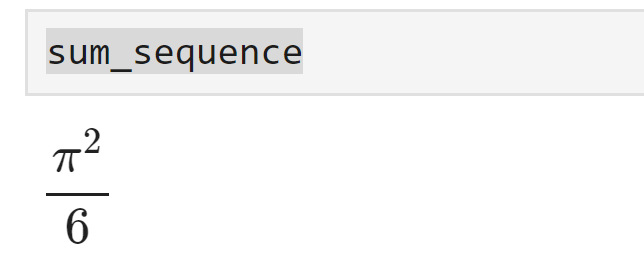
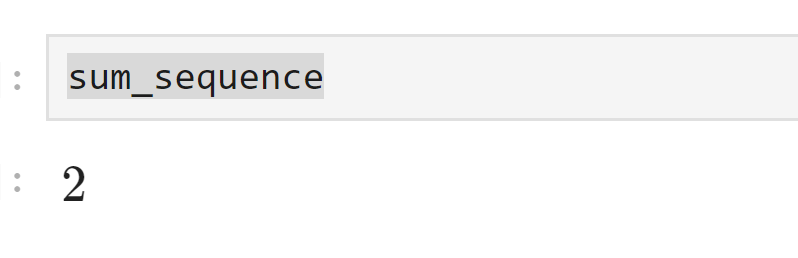
print("バーゼル問題:", sum_sequence)

出力は次のようになります。

2.6. e^xのマクローリン展開

$e^x$のマクローリン展開を\[ e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \]計算します。

n,x=sp.symbols("n x")

# 無限数列の定義
sequence = x**n/sp.factorial(n)

# 数列の無限和の計算
sum_sequence = sp.summation(sequence, (n, 0, sp.oo))

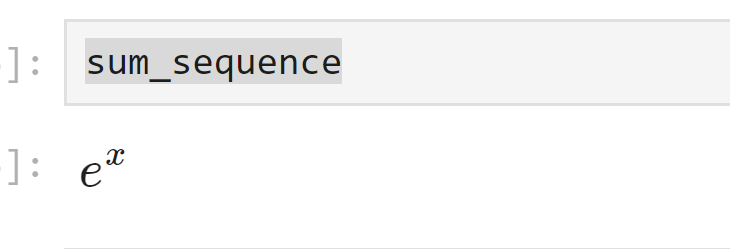
print("マクローリン展開:", sum_sequence)

出力は次のようになります。

2.7. ライプニッツ級数

ライプニッツ級数\[ 1 – \frac{1}{3} + \frac{1}{5} – \frac{1}{7} + \frac{1}{9} – \cdots = \sum_{k=0}^{\infty} \frac{(-1)^k}{2k+1} = \frac{\pi}{4} \]を計算します。

n = sp.symbols('n')
# 級数の定義
sequence = (-1)**n/(2*n+1)

# 数列の無限和の計算
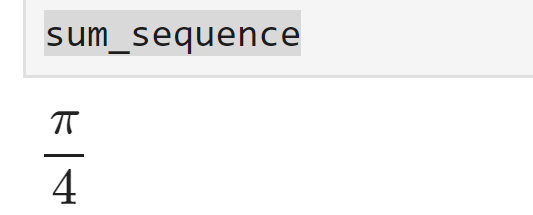
sum_sequence = sp.summation(sequence, (n, 0, sp.oo))

出力は次のようになります。

2.8. メルカトル級数

メルカトル級数\[ 1 – \frac{1}{2} + \frac{1}{3} – \frac{1}{4} +\frac{1}{5}-\frac{1}{6} +\cdots = \sum_{k=1}^{\infty} \frac{(-1)^{k-1}}{k} = \log 2 \]を計算します。

n = sp.symbols('n')
# 級数の定義
sequence = (-1)**(n-1)/n

# 数列の無限和の計算
sum_sequence = sp.summation(sequence, (n, 1, sp.oo))
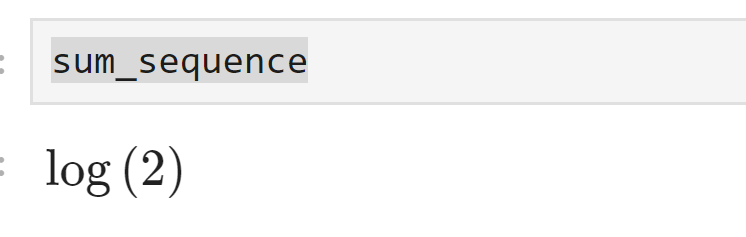
出力は次のようになります。