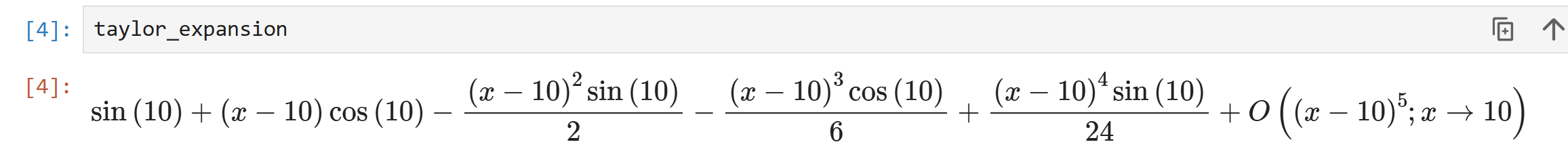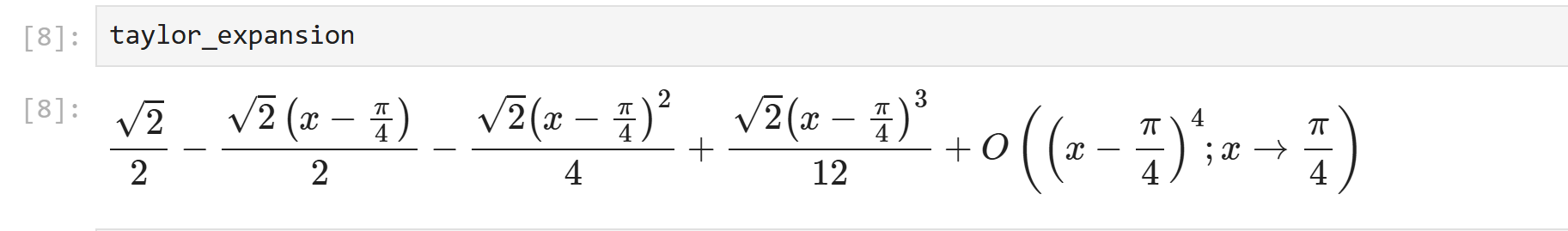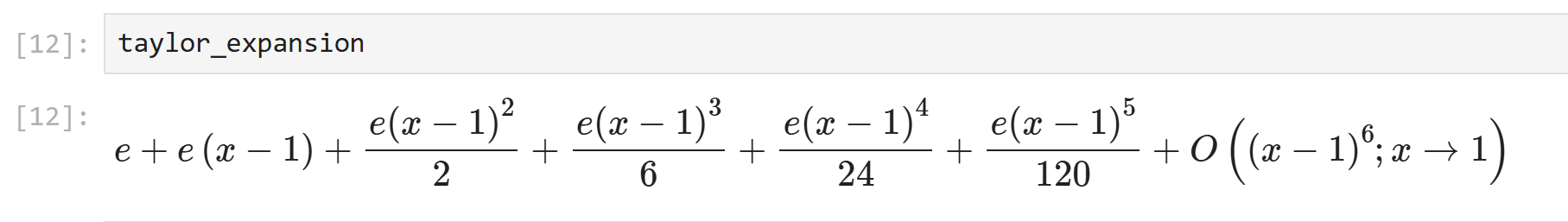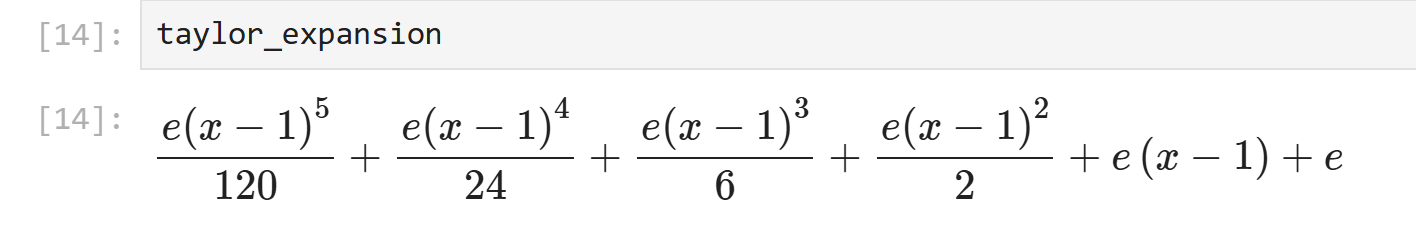【SymPy・Python】テイラー展開の計算方法のseries()について

はるか
テイラー展開。関数を多項式で近似。
ふゅか
そうそう!例えば、曲線を直線で近似するような感じよね。SymPyならPythonで簡単に試せるんだから、便利だよ!
目次
1. テイラー展開とSymPy
SymPyはPythonで利用できる数値計算ライブラリで、数式の操作や解析を簡単に行うことができます。その中でも「テイラー展開」は、関数を多項式で近似する方法として、数学や物理学、機械学習など幅広い分野で役立ちます。この記事では、SymPyを使ったテイラー展開の方法を解説します。
1.1. テイラー展開とは?
テイラー展開(Taylor Expansion)は、ある関数 \( f(x) \) を特定の点 \( a \) の近くで次のような形の多項式で表現する手法です。
\[ f(x) = f(a) + f'(a)(x-a) + \frac{f”(a)}{2!}(x-a)^2 + \frac{f^{(n)}(a)}{n!}(x-a)^n + \cdots \]
この式は、実際には有限の項で打ち切り、近似として利用します。
2. SymPyを使ったテイラー展開
SymPyでは、series関数を使ってテイラー展開を簡単に実現できます。
2.1. 基本構文
series(expression, variable, point, order)
- expression: 展開したい数式
- variable: 数式に含まれる変数
- point: 展開の基準点(例: \( a \))。0にするとマクローリン展開になります。
- order: 何次の項まで展開するか(例: 5なら4次まで展開)
2.2. 例1: \( \sin(x) \) のテイラー展開
まずは、\( \sin(x) \) を \( x =10\) を中心に4次の項まで展開します。
from sympy import symbols, series, sin
# 変数 x を定義
x = symbols('x')
# sin(x) のテイラー展開
taylor_expansion = series(sin(x), x, 10, 5)
print(taylor_expansion)
実行結果
ここで、\(O(\cdot)\) は 5 次以上の項を省略していることを意味します。
2.3. 例2:\( \cos(x) \) のテイラー展開
\( \cos(x) \) を \( x = \pi/4 \) で展開する場合は次のように書きます。
from sympy import symbols, series, cos, pi
x = symbols('x')
# cos(x) のテイラー展開(基準点 π/4)
taylor_expansion = series(cos(x), x, pi/4, 4)
print(taylor_expansion)
実行結果(近似値):
2.4. 例3: \( e^x \) のテイラー展開
次に、指数関数 \( e^x \) を \( x = 1 \) を中心に展開します。
from sympy import symbols, series, exp
x = symbols('x')
# exp(x) のテイラー展開
taylor_expansion = series(exp(x), x, 1, 6)
print(taylor_expansion)
実行結果:
3. 注意点
series関数は無限級数ではなく、指定した次数までの近似しか計算しません。- 残りの項を省略するために、\(O(\cdot)\) が結果に表示されます。この部分を取り除きたい場合は、
removeOメソッドを使います。
taylor_expansion = taylor_expansion.removeO()はるか
無限ではないことに注意。指定次数まで。
ふゅか
そうそう!だから結果に「O(⋅)」がついて、残りの項を省略してるって示すのよ。
はるか
removeOを使えば、「O(⋅)」を削除できる。
PR