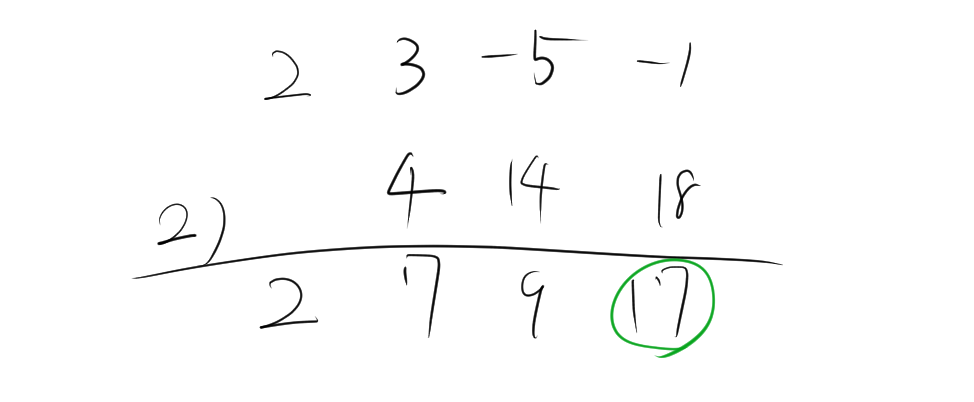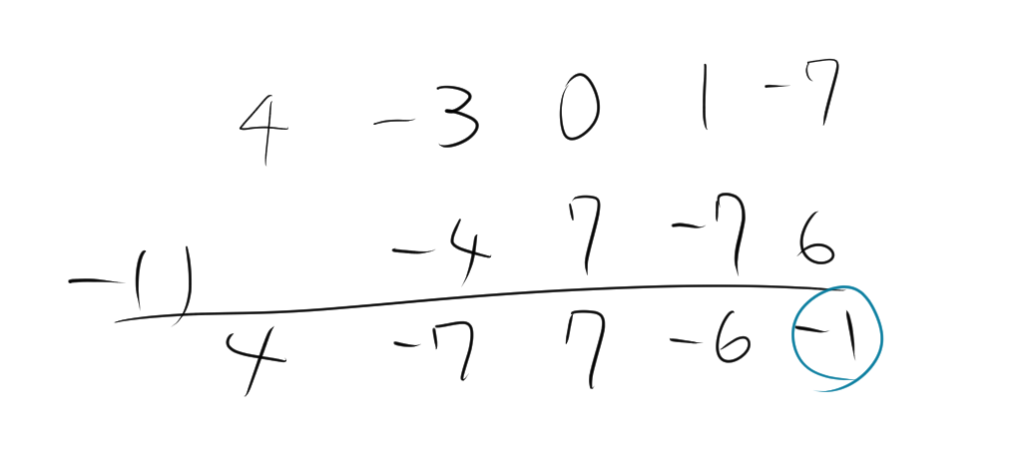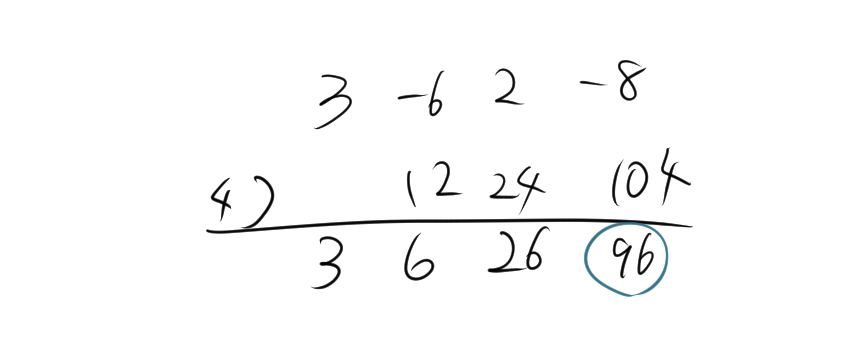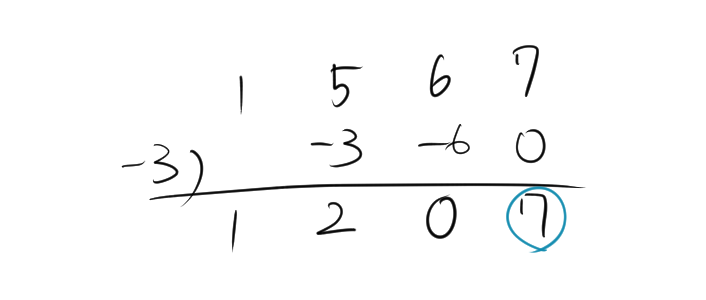組立除法の例と因数分解、４つの例題について

はるか

組立除法、係数だけ操作して割り算をする方法。

ふゅか

そうだね！多項式を1次式で割るときに便利なのよね♪

1. 組立除法とは

1.1. 組立除法の例

組立除法を使って、多項式 \( 3x^3 + 5x^2 + 7x + 100 \) を \( x – 2 \) で割りましょう。

多項式の係数は \([3, 5, 7, 100]\) です。次の手順で進めます。

• まず、最初の係数 3 をそのまま下ろします。
• 次に、3 × 2 = 6 を次の係数 5 に足します。5 + 6 = 11。
• 11 × 2 = 22 を次の係数 7 に足します。7 + 22 = 29。
• 29 × 2 = 58 を次の係数 100 に足します。100 + 58 = 158。

結果、多項式を \( x – 2 \) で割ったときの商は \( 3x^2 + 11x + 29 \)、余りは 158 です。

\[ \frac{3x^3 + 5x^2 + 7x + 100}{x – 2} = 3x^2 + 11x + 29 + \frac{158}{x – 2} \]

ふゅか

最初の係数をそのまま下ろして、次の係数に掛けて足していけば、すぐに答えが出ちゃうの！

1.2. 組立除法が成り立つ理由

ふゅか

３次式の場合で、成り立つ理由を考えてみよう！

多項式$ax^3+bx^2+cx+d$が与えられているとき、$x-r$で割ったとき、多項式は次のようになります。

$$ax^3+bx^2+cx+d = (sx^2+tx+u)(x-r)+v$$

式を展開して、移項すると次のようになります。

$$(a-s)x^3+(b-t+rs)x^2+(c-u+rt)x+(d-v+ru) =0 $$

係数を比較すると、

$$s=a,\quad t=b+rs  ,\quad u=c+rt ,\quad v=d+ru$$

ここで、$x-r$で割ったときの組立除法は次のようになります。

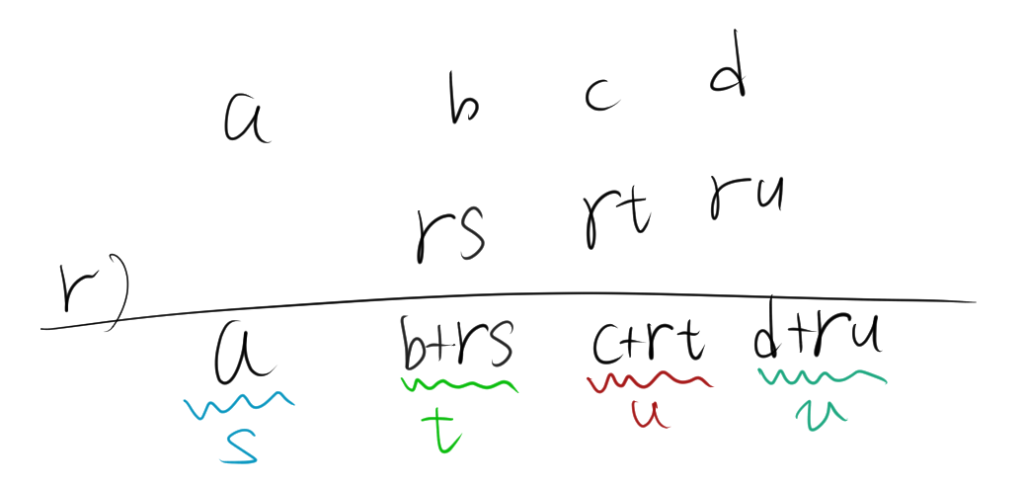したがって、求めた$s,t,u,v$と組立除法で求めた$s,t,u,v$が一致するため、組立除法は成り立つ。

2. 組立除法による因数分解

組立除法を利用して因数分解を行うことができます。

はるか

多項式を割ったときにゼロになるときを考えればよいから、組立除法が使える。

2.1. $a^3+b^3$の組み立て除法

$a$を基準に組み立て除法を行うと、

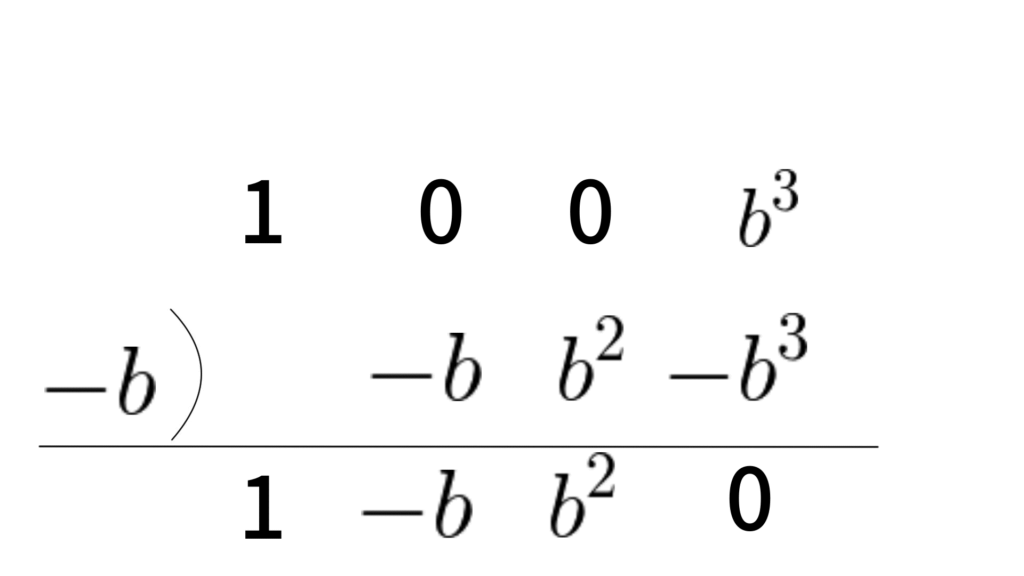
$$\begin{align*} a^3+b^3 &=\{a-(-b)\}(a^2-a^1b+a^0b^2) \\ &=(a+b)(a^2-ab+b^2) \end{align*}$$

2.2. $(a+b+c)^2$の組立て除法

$a$を基準に組み立て除法を行うと、

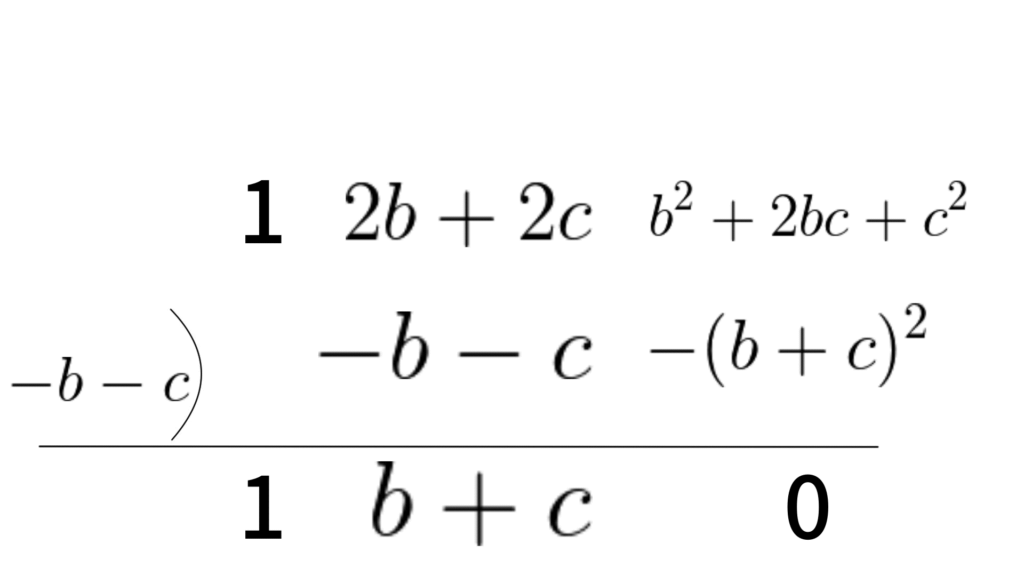
$$\begin{align*}  a^2+b^2+c^2+2ab+2bc+2ca &=\{a-(-b-c)\}\{a^1+a^0(b+c)\} \\ &=(a+b+c)(a+b+c) \\ &=(a+b+c)^2 \end{align*}$$

2.3. $a^3+b^3+c^3-3abc$の組立て除法

$a$を基準に組み立て除法を行うと、

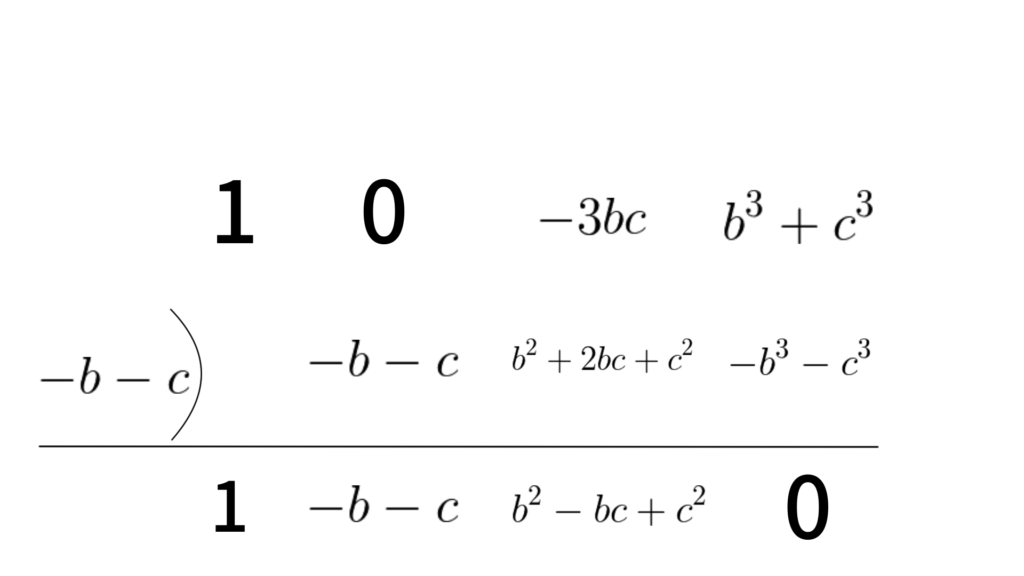
$$\begin{align*} a^3+b^3+c^3-3abc &=\{a-(-b-c)\}\{a^2+a^1(-b-c)+a^0(b^2-bc+c^2)\} \\ &=(a+b+c)(a^2-ab-ca+b^2-bc+c^2) \\ &=(a+b+c)(a^2+b^2+c^2-ab-bc-ca) \end{align*}$$

3. 例題

3.1. 例題1

1. \(x – 2\) の係数 \(2\) を組立除法に使用。
2. 被除数の係数を順に並べる: \([2, 3, -5, 1]\)。
3. 組立除法の手順に従って計算。

商 \(2x^2 + 7x + 9\)、余り \(17\)になるので、

$$\frac{2x^3 + 3x^2 – 5x + 1}{x-2}=2x^2+7x+9+\frac{17}{x-2}$$

3.2. 例題2

1. \(x + 1\) の係数 \(-1\) を組立除法に使用。
2. 被除数の係数を順に並べる: \([4, -3, 0, 1, -7]\)。
3. 組立除法の手順に従って計算。

商 \(4x^3 – 7x^2 + 7x – 6\)、余り \(-1\)になるので、

$$\frac{4x^4 – 3x^3  + x – 7}{x + 1}=4x^3 – 7x^2 + 7x – 6-\frac{1}{x + 1}$$

3.3. 例題3

1. \(x – 4\) の係数 \(4\) を組立除法に使用。
2. 被除数の係数を順に並べる: \([3, -6, 2, -8]\)。
3. 組立除法の手順に従って計算。

商 \(3x^2 + 6x + 26\)、余り \(96\)になるので、

$$\frac{3x^3 – 6x^2 + 2x – 8}{x -4}=3x^2 + 6x + 26+\frac{96}{x -4}$$

3.4. 例題4

1. \(x + 3\) の係数 \(-3\) を組立除法に使用。
2. 被除数の係数を順に並べる: \([1, 5, 6, 7]\)。
3. 組立除法の手順に従って計算。

商 \(x^2 + 2x + 0\)、余り \(7\)となるから、

$$\frac{x^3 + 5x^2 + 6x + 7}{x+3} =x^2 + 2x +\frac{7}{x+3}$$