【漸化式】n次の多項式と組立除法の考え方!組立除法が成り立つ理由について

1. 多項式と剰余について考える
n次の多項式 \( f(x) \) が次のように与えられているとします。
\[ f(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 \]
この多項式を \( x – r \) で割ったとき、剰余を \( R \) とします。つまり、次のように表されます。
\[ f(x) = (b_{n-1} x^{n-1} + b_{n-2} x^{n-2} + \cdots + b_1 x + b_0)(x – r) + R \]
ここで重要なポイントは、剰余 \( R \) は \( x \) に依存しないということです。この結果を組立除法を使って確認していきます。
組立除法の例題や計算については次の記事で解説しています。
2. 組立除法の仕組み
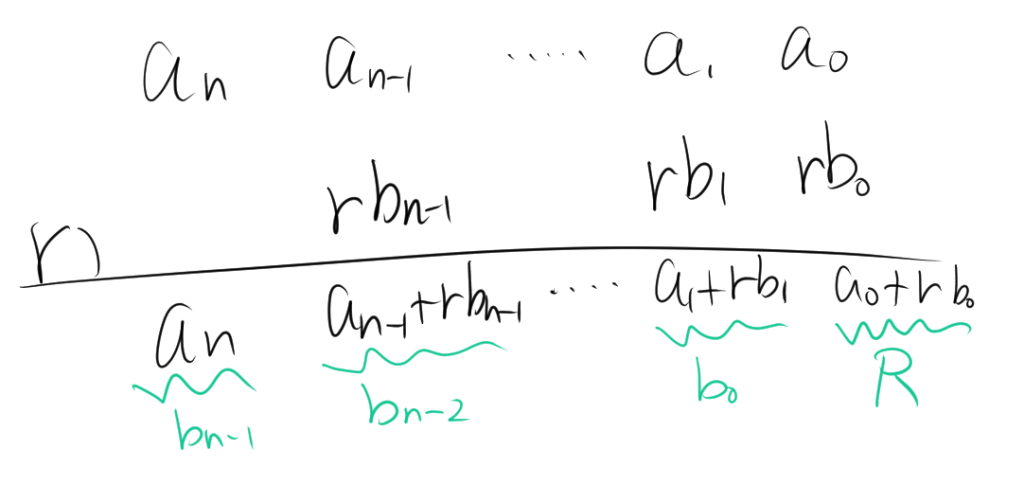
まず、与えられた多項式の係数を順番に並べます。
\[ [a_n, a_{n-1}, \cdots, a_1, a_0] \]
これを使って、組立除法を進めていきます。
まず、最初の係数 \( b_{n-1} \) は \( a_n \) に等しいです。
\[ b_{n-1} = a_n \]
次に、2番目の係数 \( b_{n-2} \) は次のように求められます。
\[ b_{n-2} = a_{n-1} + r b_{n-1} = a_{n-1} + r a_n \]
この手順をさらに進めて、3番目の係数 \( b_{n-3} \) を求めます。
\[\begin{align*} b_{n-3}& = a_{n-2} + r b_{n-2} \\&= a_{n-2} + r(a_{n-1} + r a_n) \\&= r^2 a_n + r a_{n-1} + a_{n-2}\end{align*} \]
この計算を続けていくと、最終的には \( b_0 \) が次の形で表されます。
\[ b_0 = r^{n-1} a_n + r^{n-2} a_{n-1} + \cdots + r a_2 + a_1 \]
2.1. 剰余の計算
次に剰余 \( R \) を考えます。組立除法を使って、剰余は次のように計算されます。
\[\begin{align*} R &= r b_0 + a_0 \\&=r^n a_n + r^{n-1} a_{n-1} + \cdots + r^2 a_2 + r a_1 + a_0 \\&=f(r)\end{align*} \]
この結果、剰余 \( R \) は多項式 \( f(x) \) の \( x = r \) における値 \( f(r) \) になります。剰余の定理より、$f(r)$は多項式$f(x)$を$x-r$で割ったあまりになるから、組立除法で求めた余りは正しいことがわかる。
2.2. 組立除法と係数
最後に、組立除法によって求めた商 \( b_{n-1}, b_{n-2}, \cdots, b_0 \) と元の多項式の係数の対応を確認します。
\[ f(x) = (x – r)(b_{n-1} x^{n-1} + b_{n-2} x^{n-2} + \cdots + b_1 x + b_0) + R \]
この式の \( x^{n-i} \) の係数は次のようになります。
\[ -r b_{n-i} + b_{n-(i-1)} \]
一方で、組立除法より、$b_{n-(i-1)} = a_{n-i} + r b_{n-i}$であるから、
\[ -r b_{n-i} + b_{n-(i-1)} = a_{n-i} \]
これは、元の多項式 \( f(x) \) の$x^{n-i}$の項の係数と一致しています。このようにして、組立除法は元の多項式の係数を正しく反映していることが確認できます。