【一次不等式】連立不等式の解き方と3つの例題について

ふゅか

連立一次不等式って、同時に二つ以上の不等式を解くんだよね！

はるか

複数の不等式を解くから、時々解が存在しない場合もある。

1. 一次不等式

一次不等式は、一次方程式と似ていますが、「=」の代わりに「<」「>」「$\geqq$」「$\leqq$」などの不等号を用います。次のような形です。

\[ ax + b < c \]

ここで、\(x\)は変数で、\(a\)、\(b\)、\(c\)は定数です。この不等式は、特定の範囲の\(x\)に対して成立します。数直線を利用して、解の範囲を図示することで解きやすくなります。

はるか

一次不等式って、単純な不等式だね。xの範囲を決めるだけ。

ふゅか

そうそう！「=」じゃなくて、「<」とか「>」とかで範囲が決まるから、簡単だけど、ちょっとしたコツがいるよね！

2. 連立一次不等式

連立一次不等式は、複数の一次不等式を同時に解くものです。例えば、次のような不等式を考えます。

\[ \begin{cases} 2x – 3 > 1 \\ x + 4 \leq 6 \end{cases} \]

この場合、2つの不等式が同時に成り立つ範囲の\(x\)を求めることが目標です。

1つ目の不等式 \(2x – 3 > 1\) は、まず \(x\)の範囲を求めるために次のように解きます。

$$\begin{align*} 2x &> 4 \\ x &> 2 \end{align*}$$

次に、2つ目の不等式 \(x + 4 \leqq 6\) を解くと、

\[ x \leqq 2 \]

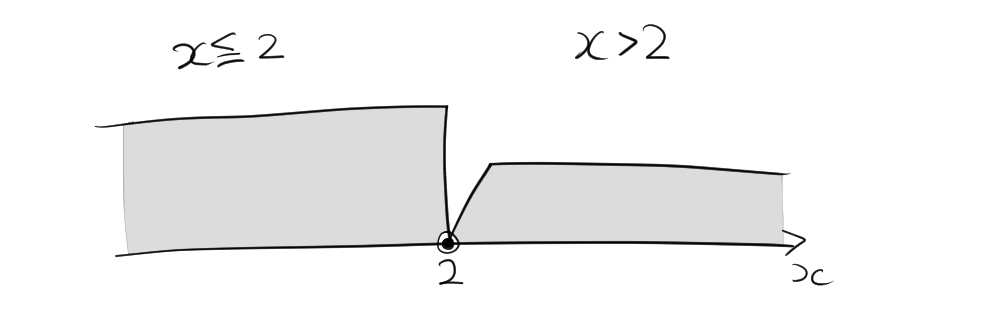
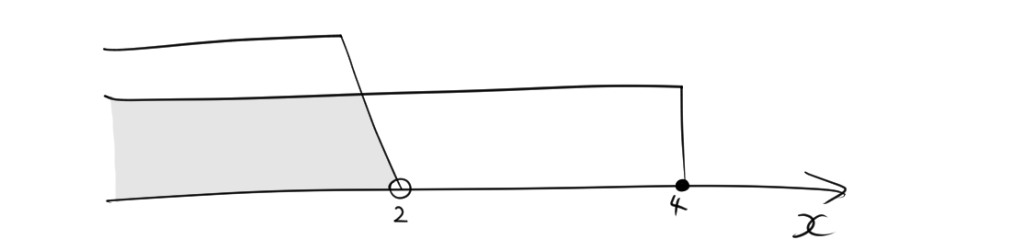
これら2つの不等式を同時に満たす\(x\)は、\(x > 2\) かつ \(x \leqq 2\) です。この場合、解が矛盾しているため、解は存在しません。

3. 不等式の例題

3.1. 例題１

1つ目の不等式は、

\[ x \geqq -1 \]

2つ目の不等式は、

\[ x < 4 \]

これらを満たす解の範囲は、\(-1 \leqq x < 4\) です。この解は数直線上で表すと、次のようになります。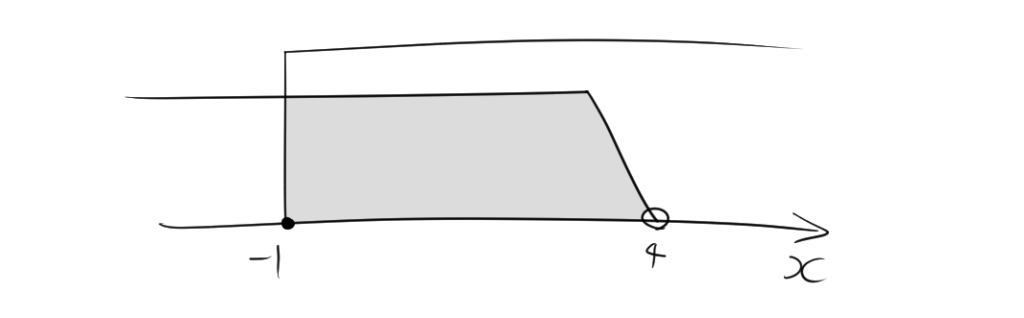

3.2. 例題 2

1つ目の不等式を解きます。

$$\begin{align*} 4x – 3 &> 5 \\ 4x &> 8 \\ x &> 2 \end{align*}$$

次に、2つ目の不等式を解きます。

$$\begin{align*} x + 2 &\leqq 6 \\ x &\leqq 4 \end{align*}$$

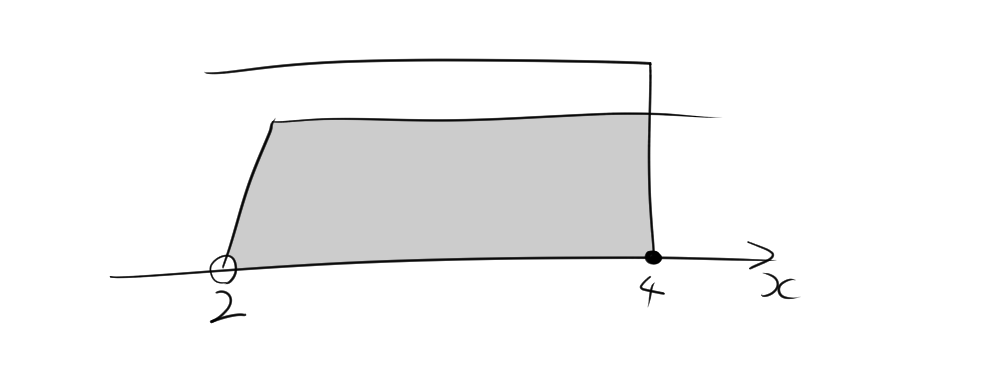
これらを満たす \(x\) は、\(2 < x \leqq 4\) です。解の範囲は次の通りです。 \[ 2 < x \leqq 4 \]

3.3. 例題 3

1つ目の不等式を解きます。

$$\begin{align*} -2x + 5 &\geqq 1 \\ -2x &\geqq -4 \\ x &\leqq 2 \end{align*}$$

次に、2つ目の不等式を解きます。

$$\begin{align*} x – 1 &< 3 \\ x &< 4 \end{align*}$$

これらを満たす \(x\) は、\(x \leqq 2\) かつ \(x < 4\) です。したがって、解の範囲は次の通りです。 \[ x \leqq 2 \]