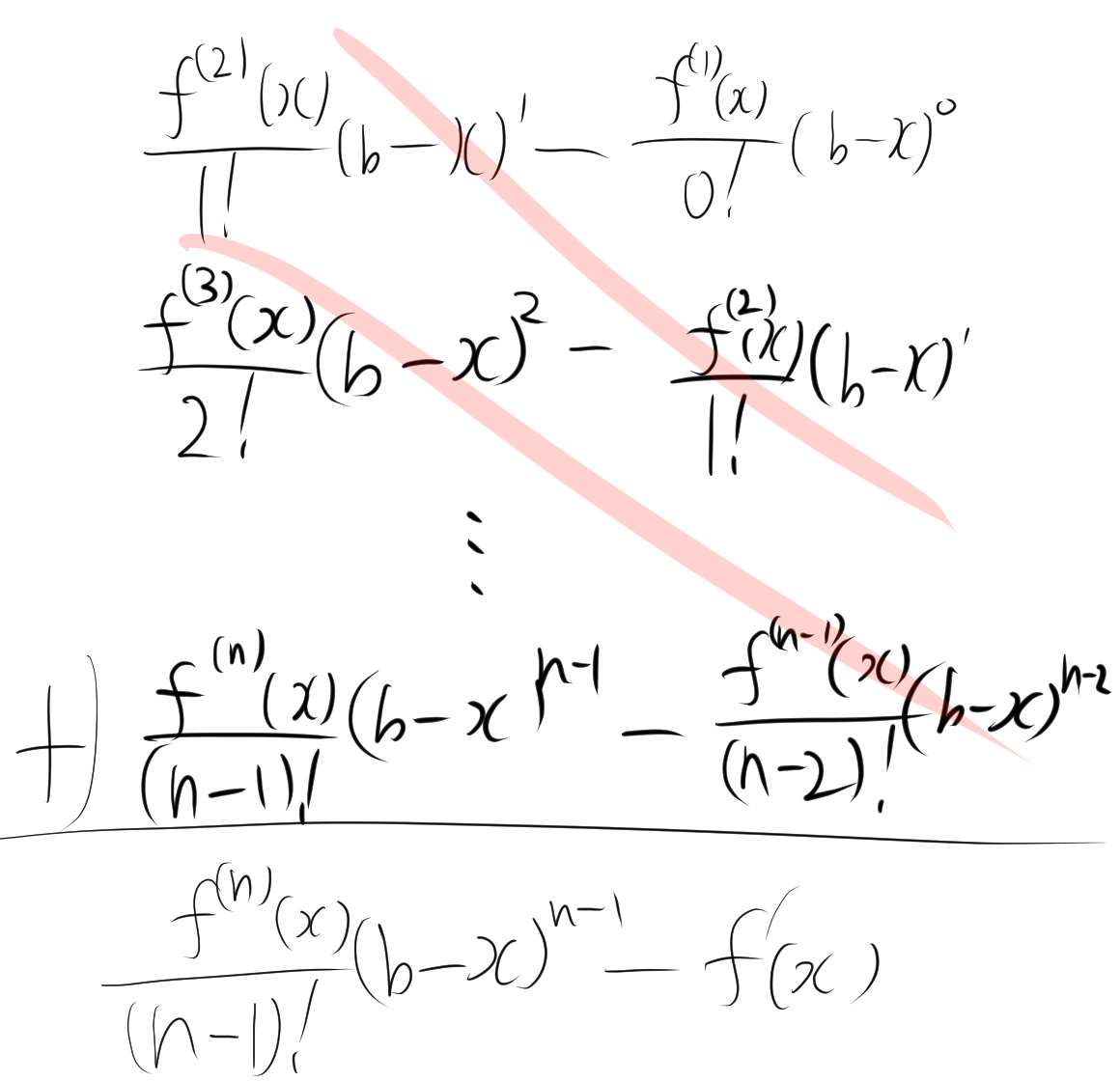テイラーの定理とテイラー展開

1. テイラーの定理
\[ f(x) = \displaystyle\sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k + R_n(x) \]
ここで、\( R_n(x) \) は剰余項(誤差項)で、\( n \) 次のテイラー多項式による近似と実際の関数値との差を表します。
1.1. 剰余項の形式
剰余項 \( R_n(x) \) にはいくつかの形があり、今回はラグランジュの剰余項を使用します。
\[ R_n(x) = \frac{f^{(n)}(c)}{n!} (x-a)^{n} \]
ここで$ a<c<x$を満たすcが存在する。
2. テイラーの定理の証明
テイラーの定理の証明について、ロルの定理を用いたアプローチで解説します。
$f(b)$を次のように定義する。
$$f(b)=\displaystyle\sum^{n}_{k=0} \dfrac{f^{(k)}}{k!} (b-a)^k+\dfrac{K}{(n+1)!}(b-a)^{n+1}$$
関数 \( g(x) \) を以下のように定義します。
\[
g(x) = f(b) – f(x) – \sum_{k=1}^{n-1} \frac{f^{(k)}(x)}{k!} (b-x)^k – K \frac{(b-x)^n}{n!}
\]
ただし、$f(x)$は$f(b)$の$b$を$x$に置き換えた関数である。
ポイント
ここで、\(K\) を求めることを目標とします。
- \( g(a) = 0 \): \(A\) の選び方により、\( g(a) = 0 \) が保証されます。
- \( g(b) = 0 \): 直接代入すると、\( g(b) = f(b) – f(b) – 0 – 0 = 0 \) となります。
\( g(a) = 0 \) かつ \( g(b) = 0 \) であり、\( g(x) \) は \( [a, b] \) で連続、\( (a, b) \) で微分可能であるため、ロルの定理より、ある \( c \)(\( a < c < b \))が存在して \( g'(c) = 0 \) となります。
次に\( g'(x) \) の計算を行う。
\[
g'(x) = -f'(x) + \sum_{k=1}^{n-1} \left[\frac{f^{(k+1)}(x)}{k!} (b-x)^k – \frac{f^{(k)}(x)}{(k-1)!} (b-x)^{k-1}\right] – K\frac{n(b-x)^{n-1}}{n!}
\]
各項を整理すると、ほとんどの項が打ち消し合い、最終的に
\[
g'(x) = \frac{f^{(n)}(x)}{(n-1)!}(b-x)^{n-1} – K\frac{(b-x)^{n-1}}{(n-1)!}
\]
になります。
ロルの定理により、\( g'(c) = 0 \) なので、
\[
K = f^{(n)}(c)
\]
が得られます。
以上の手順で、剰余項の \( K \) は \( f^{(n)}(c) \) に等しくなります。
2.1. 項の打ち消し合い
シグマの項の打ち消し合いの部分に注目すると次のようになります。
もっと詳しく知りたい方は次の記事で!
3. テイラーの定理からテイラー展開
\[ \displaystyle\lim_{n \to \infty} R_n(x) = 0 \]
このとき、関数 \( f(x) \) は次のように無限和で表されます。
\[ f(x) = \displaystyle\sum_{k=0}^{\infty} \frac{f^{(k)}(a)}{k!} (x-a)^k \]
4. テイラーの定理の応用例
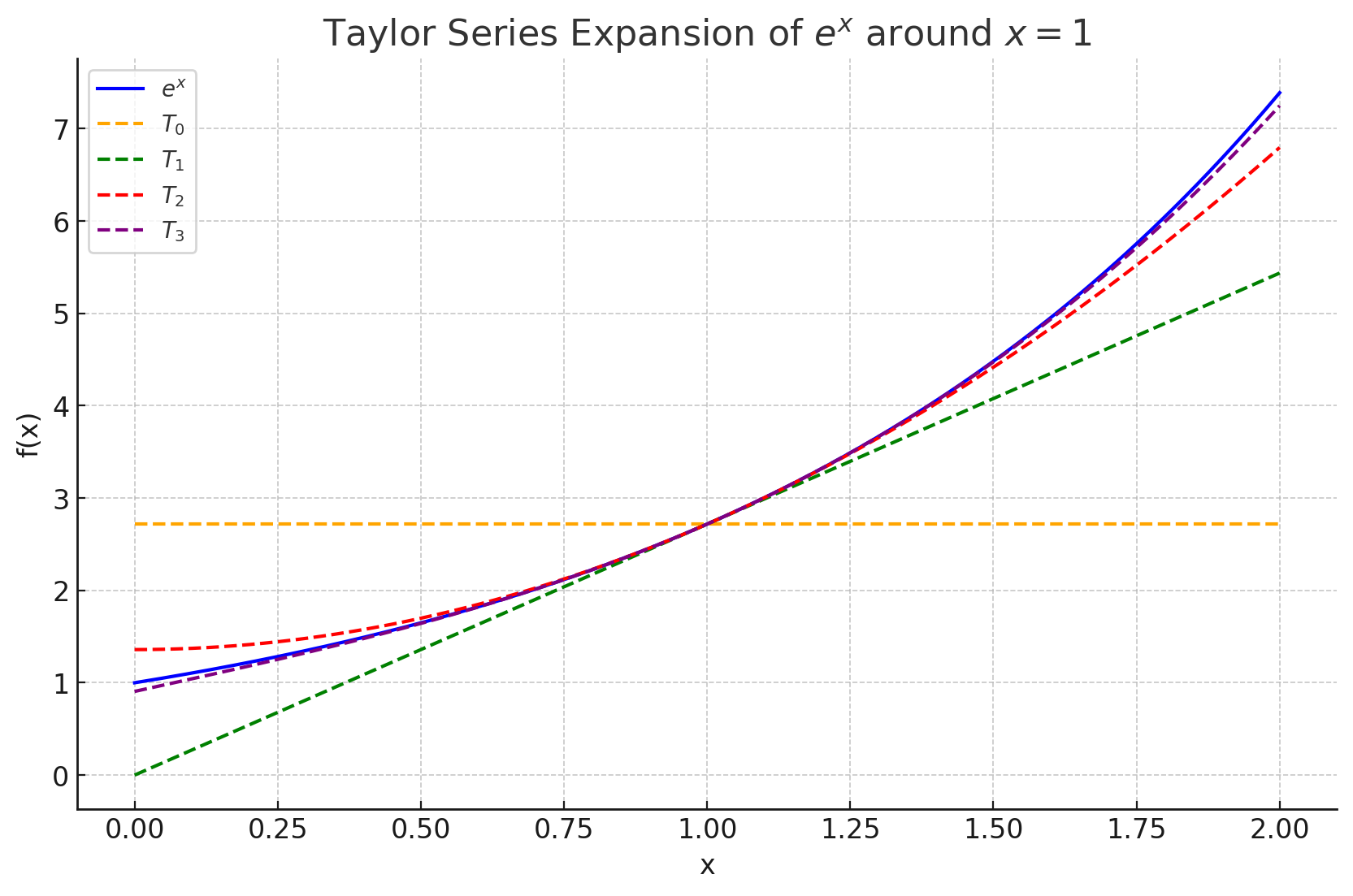
こちらのグラフは、 \( e^x \) の \( x = 1 \) でのテイラー展開を示しています。
- 青い実線は元の関数 \( e^x \) を表しています。
- オレンジの破線は0次のテイラー展開 \( T_0 \) で、これは定数 \( e \) に相当します。
- 緑の破線は1次のテイラー展開 \( T_1 \) で、これは一次近似を表しています。
- 赤い破線は2次のテイラー展開 \( T_2 \) で、これは二次近似であり、より正確な近似を提供します。
- 紫の破線は3次のテイラー展開 \( T_3 \) で、さらに高精度な近似を表します。
このグラフから分かるように、テイラー展開の次数が高くなるほど、関数 \( e^x \) に対する近似の精度が上がり、特に \( x = 1 \) の近くでは元の関数とよく一致しています。