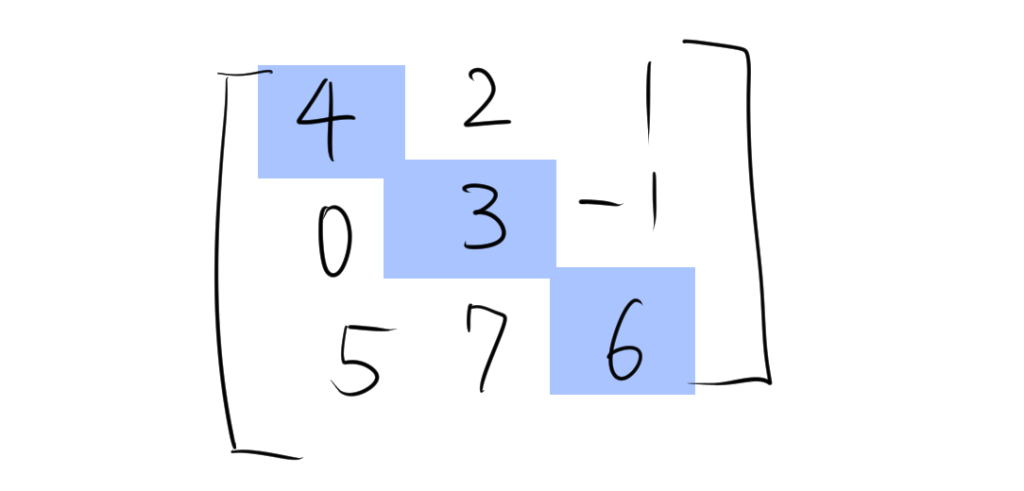更新:2024/09/17

行列のトレース（tr）の定義・4つの性質・例題について

$はるか$

はるか

トレースって、行列の対角要素の合計。

1. トレースとは
2. トレースの性質
2.1. 線形性
2.2. 可換
2.3. 相似変換
2.4. 固有値の総和
3. 例題
3.1. 例題1：トレースの計算
3.2. 例題2：可換の性質
3.3. 例題3：行列の和のトレース
3.4. 例題 4: スカラー倍の行列のトレース

1. トレースとは

$ \text{tr} $（トレース）とは、正方行列の対角要素の総和を指します。行列 $ A $ が $ n \times n $ の正方行列であるとき、そのトレース $ \text{tr}(A) $ は次のように定義されます。

\[ \text{tr}(A) = a_{11} + a_{22} + \cdots + a_{nn} \]

ここで、$ a_{ii} $ は行列 $ A $ の対角成分、つまり行番号と列番号が等しい成分です。

2. トレースの性質

$ふゅか$

ふゅか

トレースには面白い性質があるのよ！例えば、トレースの和と積で線形性があるわ！

2.1. 線形性

行列 $ A $ と $ B $ およびスカラー $ c $ に対して、

\[ \text{tr}(A + B) = \text{tr}(A) + \text{tr}(B) \]

\[ \text{tr}(cA) = c \cdot \text{tr}(A) \]

行列 $ A $ と $ B $ が $ n \times n $ の場合、それぞれのトレースは行列の対角要素の和で表されます。

\[ \text{tr}(A) = \sum_{i=1}^{n} a_{ii}, \quad \text{tr}(B) = \sum_{i=1}^{n} b_{ii} \]

まず、和に関して性質を示す。

行列 $ A + B $ のトレースは、$ A + B $ の対角要素の和です。

\[ \text{tr}(A + B) = \sum_{i=1}^{n} (a_{ii} + b_{ii}) \]

対角要素の和を分配法則を使って分けると、

\[ \text{tr}(A + B) = \sum_{i=1}^{n} a_{ii} + \sum_{i=1}^{n} b_{ii} \]

これは $ A $ と $ B $ のトレースの和と等しいので、

\[ \text{tr}(A + B) = \text{tr}(A) + \text{tr}(B) \]

次に、スカラー倍に関して性質を示す。

行列 $ A $ をスカラー $ c $ で掛けた行列 $ cA $ のトレースは、対角要素を $ c $ 倍したものの和になります。

\[ \text{tr}(cA) = \sum_{i=1}^{n} (c \cdot a_{ii}) \]

この和は、スカラー $ c $ を前に出して書くことができるので、

\[ \text{tr}(cA) = c \cdot \sum_{i=1}^{n} a_{ii} \]

これは $ c $ と $ A $ のトレースの積に等しいです。

\[ \text{tr}(cA) = c \cdot \text{tr}(A) \]

2.2. 可換

行列 $ A $ と $ B $ に対して、

\[ \text{tr}(AB) = \text{tr}(BA) \]

まず、行列 $ A $ と $ B $ をそれぞれ $ n \times n $ 行列とします。行列の積 $ AB $ および $ BA $ はそれぞれ $ n \times n $ 行列になります。

行列 $ AB $ の$(i,j)$成分 $ (AB)_{ij} $ は次のように定義されます。

\[ (AB)_{ij} = \sum_{k=1}^{n} A_{ik} B_{kj}\]

同様に、行列 $ BA $ の成分 $ (BA){ij} $ は次のように定義されます。

\[ (BA)_{ij} = \sum_{k=1}^{n} B_{ik} A_{kj}\]

行列のトレース（$\text{tr}$）は、対角成分の和です。したがって、

\[ \text{tr}(AB) = \sum_{i=1}^{n} (AB)_{ii} = \sum_{i=1}^{n} \sum_{k=1}^{n} A_{ik} B_{ki} \]

同様に、

\[ \text{tr}(BA) = \sum_{i=1}^{n} (BA)_{ii} = \sum_{i=1}^{n} \sum_{k=1}^{n} B_{ik} A_{ki} \]

ここで、$\text{tr}(AB)$ と $\text{tr}(BA)$ を比べてみます。上記の式を入れ替えてみると、

\[ \text{tr}(AB) = \sum_{i=1}^{n} \sum_{k=1}^{n} A_{ik} B_{ki} \]

\[ \text{tr}(BA) = \sum_{k=1}^{n} \sum_{i=1}^{n} B_{ki} A_{ik}\]

これらの二重和の順序を入れ替えても和の値は変わりません。したがって、

\[ \text{tr}(BA) = \sum_{i=1}^{n} \sum_{k=1}^{n} A_{ik} B_{ki} \]

よって、 \[ \text{tr}(AB) = \text{tr}(BA). \]

このように、行列 $ A $ と $ B $ に対して $\text{tr}(AB) = \text{tr}(BA)$ であることが示されました。

2.3. 相似変換

行列のトレースは、相似変換によって変わりません。

\[ \text{tr}(P^{-1}AP) = \text{tr}(A) \]

\[ \text{tr}(AB) = \text{tr}(BA) \]

より、Aの部分を$P^{-1}A$、Bの部分を$P$とすると、

\[ \text{tr}(P^{-1}AP) = \text{tr}(PP^{-1}A) \]

$$=\text{tr}(EA) $$

$$=\text{tr}(A) $$

したがって、トレースは、相似変換によって変わらない。

\[ \text{tr}(P^{-1}AP) = \text{tr}(A) \]

2.4. 固有値の総和

トレースは行列の固有値の総和とも一致します。行列 $ A $ の固有値を $ \lambda_1, \lambda_2, \ldots, \lambda_n $ とすると、 \[ \text{tr}(A) = \lambda_1 + \lambda_2 + \cdots + \lambda_n \]

3. 例題

3.1. 例題1：トレースの計算

次の行列 $ A $ のトレースを求めなさい。

\[ A = \begin{bmatrix} 4 & 2 & 1 \\ 0 & 3 & -1 \\ 5 & 7 & 6 \end{bmatrix} \]

行列 $ A $ のトレース $ \text{tr}(A) $ は、対角要素の和です。

対角要素を取り出します。

1行1列目の要素：$ 4 $
2行2列目の要素：$ 3 $
3行3列目の要素：$ 6 $

対角要素の和を計算します： \[ \text{tr}(A) = 4 + 3 + 6 = 13 \]

したがって、行列 $ A $ のトレースは $ 13 $ です。

3.2. 例題2：可換の性質

次の行列 $ A $ と $ B $ を考えます。

\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \]

行列 $ AB $ を計算し、そのトレース $\text{tr}(AB)$ を求めてください。
行列 $ BA $ を計算し、そのトレース $\text{tr}(BA)$ を求めてください。
$\text{tr}(AB)$ と $\text{tr}(BA)$ が等しいことを確認してください。

行列 $ AB $ を計算します。

\[ AB = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 \times 0 + 2 \times 1 & 1 \times 1 + 2 \times 0 \\ 3 \times 0 + 4 \times 1 & 3 \times 1 + 4 \times 0 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 4 & 3 \end{bmatrix} \]

トレース $\text{tr}(AB)$ は対角要素の和です。

\[ \text{tr}(AB) = 2 + 3 = 5 \]

行列 $ BA $ を計算します。

\[ BA = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 0 \times 1 + 1 \times 3 & 0 \times 2 + 1 \times 4 \\ 1 \times 1 + 0 \times 3 & 1 \times 2 + 0 \times 4 \end{bmatrix} = \begin{bmatrix} 3 & 4 \\ 1 & 2 \end{bmatrix} \]

トレース $\text{tr}(BA)$ は対角要素の和です。

\[ \text{tr}(BA) = 3 + 2 = 5 \]

$\text{tr}(AB)$ と $\text{tr}(BA)$ が等しいか確認します。

\[ \text{tr}(AB) = 5, \quad \text{tr}(BA) = 5 \]

したがって、$\text{tr}(AB) = \text{tr}(BA)$ が成立することを確認できました。

3.3. 例題3：行列の和のトレース

次の行列 $ A $ と $ B $ に対して、トレースの性質 $\text{tr}(A + B) = \text{tr}(A) + \text{tr}(B)$ を確認してください。行列 $ A $ と $ B $ は次のとおりです。

\[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} \]

$ A $ と $ B $ のトレースをそれぞれ計算します。

$\text{tr}(A) = 1 + 4 = 5$

$\text{tr}(B) = 5 + 8 = 13$

$ A + B $ を計算します。 \[ A + B = \begin{pmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \end{pmatrix} = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix} \]

$ A + B $ のトレースを計算します。

$\text{tr}(A + B) = 6 + 12 = 18$

$ \text{tr}(A) + \text{tr}(B) $ を計算します。

$ 5 + 13 = 18 $

したがって、

\[ \text{tr}(A + B) = 18 = \text{tr}(A) + \text{tr}(B) \]

3.4. 例題 4: スカラー倍の行列のトレース

次の行列 $ A $ とスカラー $ c $ に対して、トレースの性質 $\text{tr}(cA) = c \cdot \text{tr}(A)$ を確認してください。行列 $ A $ とスカラー $ c $ は次のとおりです。

\[ A = \begin{pmatrix} 2 & -1 \\ 0 & 3 \end{pmatrix}, \quad c = 4 \]

$ A $ のトレースを計算します。

$\text{tr}(A) = 2 + 3 = 5$

$ cA $ を計算します。 \[ cA = 4 \cdot \begin{pmatrix} 2 & -1 \\ 0 & 3 \end{pmatrix} = \begin{pmatrix} 8 & -4 \\ 0 & 12 \end{pmatrix} \]

$ cA $ のトレースを計算します。

$\text{tr}(cA) = 8 + 12 = 20$

$ c \cdot \text{tr}(A) $ を計算します。

$ 4 \cdot 5 = 20 $

したがって、

\[ \text{tr}(cA) = 20 = c \cdot \text{tr}(A) \]

ホームに戻る