トレフォイロイド曲線の面積、弧長、アニメーションについて
1. トレフォイロイド曲線とは
\[ x = a \left(4 \cos \theta – \cos4 \theta\right) \]
\[ y = a \left(4 \sin \theta – \sin4 \theta\right) \]
1.1. アニメーション
トレフォイロイドは、内側の円が外側の円のちょうど3倍の半径を持つときに形成される特別なエピサイクロイドです。
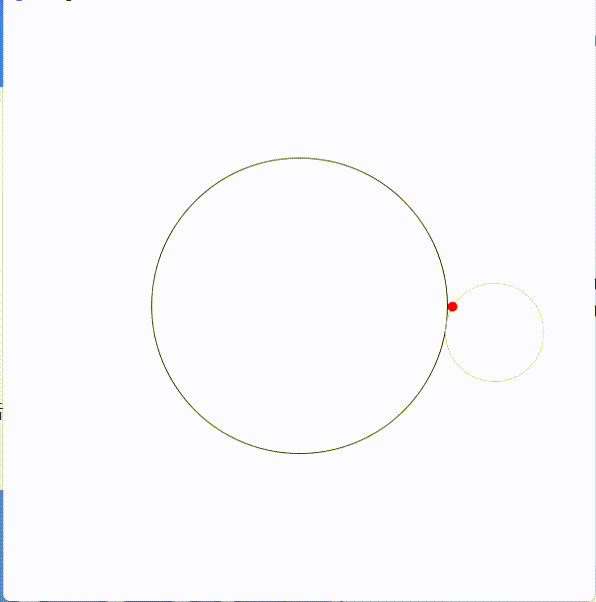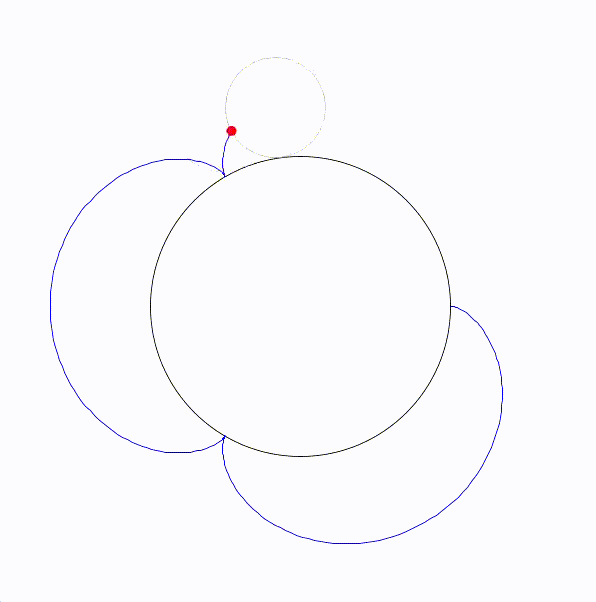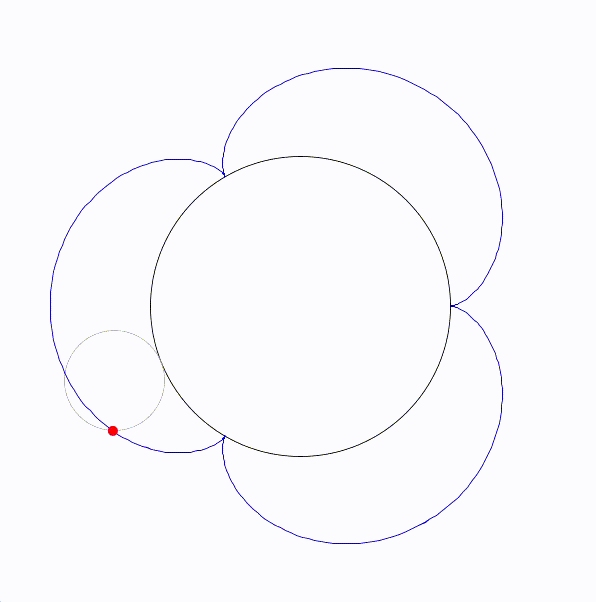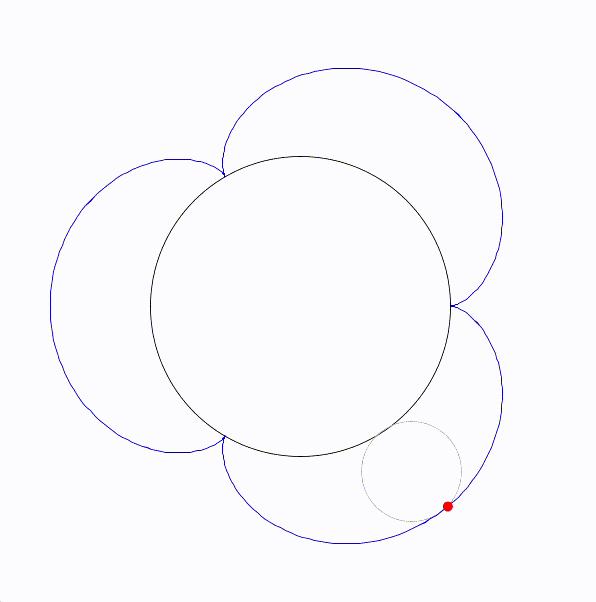定円と動く円の半径の比が1:1のとき、カージオイドと呼ばれ、半径が1:2のとき、ネフロイドと呼ばれる。
2. トレフォイロイド曲線の性質
2.1. 曲線の長さ
$$L=32a$$
まず、 \( x \) と \( y \) の \(\theta\) に関する微分を計算します。
\[ \frac{dx}{d\theta} = a \left( -4 \sin \theta + 4 \sin 4\theta \right) \]
\[ \frac{dy}{d\theta} = a \left( 4 \cos \theta – 4 \cos 4\theta \right) \]
媒介変数表示の弧長の公式より、
\[ L = \int_{0}^{2\pi} \sqrt{\left( a \left( -4 \sin \theta + 4 \sin 4\theta \right) \right)^2 + \left( a \left( 4 \cos \theta – 4 \cos 4\theta \right) \right)^2 } \, d\theta \]
\[ = a \int_{0}^{2\pi} \sqrt{16 \sin^2 \theta – 32 \sin \theta \sin 4\theta + 16 \sin^2 4\theta + 16 \cos^2 \theta – 32 \cos \theta \cos 4\theta + 16 \cos^2 4\theta} \, d\theta \]
三角関数の関係式 \( \sin^2 \theta + \cos^2 \theta = 1 \) と \( \sin^2 4\theta + \cos^2 4\theta = 1 \) を使います。
\[ L = a \int_{0}^{2\pi} \sqrt{16 (\sin^2 \theta + \cos^2 \theta) + 16 (\sin^2 4\theta + \cos^2 4\theta) – 32 (\sin \theta \sin 4\theta + \cos \theta \cos 4\theta)} \, d\theta \]
ここで、加法定理 \( \sin \theta \sin 4\theta + \cos \theta \cos 4\theta = \cos (4\theta – \theta) = \cos 3\theta \) なので、
\[ L = a \int_{0}^{2\pi} \sqrt{16 \times 2 – 32 \cos 3\theta} \, d\theta \]
\[ L = 4a \int_{0}^{2\pi} \sqrt{2 (1 – \cos 3\theta)} \, d\theta \]
半角の公式を使います。
\[ 1 – \cos 3\theta = 2 \sin^2 \frac{3\theta}{2} \]
これを代入すると、
\[ L = 4a \int_{0}^{2\pi} \sqrt{4 \sin^2 \frac{3\theta}{2}} \, d\theta \]
\[ = 8a \int_{0}^{2\pi} \left| \sin \frac{3\theta}{2} \right| \, d\theta \]
\[ = 3 \cdot 8a \int_{0}^{\frac{2\pi}{3}} \sin \frac{3\theta}{2} \, d\theta \]
\[ = 24a\left[\frac{2}{3}(-\cos\frac{3}{2}\theta)\right]^{\frac{2}{3}\pi}_{0} \]
\[ = 24a \cdot\frac{4}{3} = 32a \]
したがって、弧長は \( 32a \) です。
2.2. 曲線の囲まれた面積
$$A=20\pi a^2$$
囲まれた領域の面積を求めるために、ガウス・グリーンの定理を使用します。
媒介変数表示された曲線によって囲まれる面積 \( A \) を求めるための公式は次の通りです。
\[ A = \frac{1}{2} \int_{0}^{2\pi} [x(\theta) y'(\theta) – y(\theta) x'(\theta)] \, d\theta \]
\( x(\theta) \) と \( y(\theta) \) を \( \theta \) で微分します。
\[ x'(\theta) = a [-4\sin\theta + 4\sin4\theta] \]
\[ y'(\theta) = a [4\cos\theta – 4\cos4\theta] \]
\( x(\theta) y'(\theta) – y(\theta) x'(\theta) \) を計算する。
$$x(\theta) y'(\theta) – y(\theta) x'(\theta)$$
$$=a^2 \{ (4\cos\theta – \cos4\theta)(4\cos\theta – 4\cos4\theta) – (4\sin\theta – \sin4\theta)(-4\sin\theta + 4\sin4\theta) \}$$
$$=a^2\{ 16(\cos^2\theta+\sin^2\theta)-20(\cos\theta\cos 4\theta + \sin\theta \sin 4\theta)+4(\cos^2 4\theta + \sin^2 4\theta) \}$$
加法定理より、\( \sin \theta \sin 4\theta + \cos \theta \cos 4\theta = \cos (4\theta – \theta) = \cos 3\theta \) なので、
$$=a^2(20-\cos 3 \theta)$$
0 から \( 2\pi \) まで積分する。
\[ A = \frac{1}{2} \int_{0}^{2\pi} 20a^2 [1 – \cos3\theta] \, d\theta = 10a^2 \int_{0}^{2\pi} [1 – \cos3\theta] \, d\theta \]
\[ =10a^2 \left( \int_{0}^{2\pi} 1 \, d\theta – \int_{0}^{2\pi} \cos3\theta \, d\theta \right) \]
$$= 20\pi a^2$$
