三角形の面積の公式一覧
目次
1. 底辺と高さを用いて面積を求める
三角形の面積をS、底辺をW、高さをHとすると、
$$S=\dfrac{WH}{2}$$
となります。いわゆる、$底辺×高さ÷2$です。
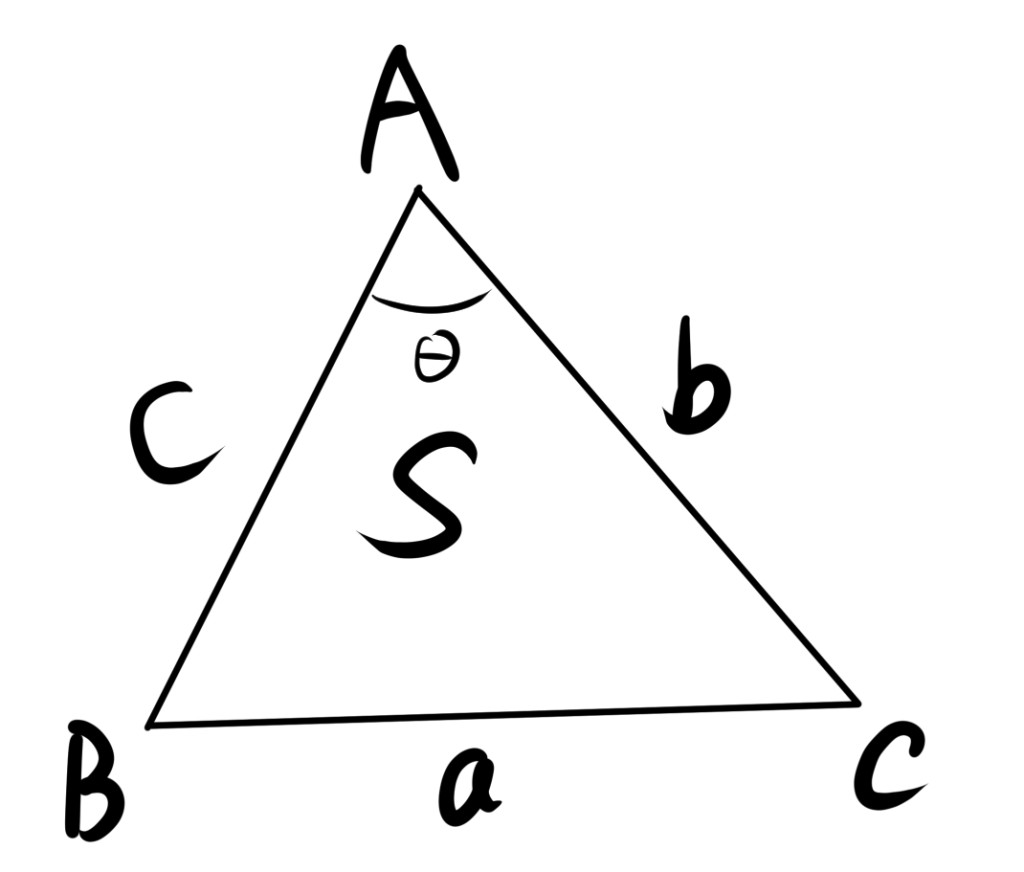
2. $\sin\theta$を用いて三角形の面積を求める
$$S=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B$$
詳しくはこちらの記事で解説しています。
3. ヘロンの公式を用いて三角形の面積を求める
$S = \sqrt{s(s-a)(s-b)(s-c)}$
$S =\dfrac{1}{4}\sqrt{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}$
ここで、$S$は三角形の面積、$a$,$b$,$c$はそれぞれ三角形の3辺の長さを表し、$s$は次のように定義されます。
$s = \dfrac{a+b+c}{2}$
詳しくはこちらの記事で解説しています。
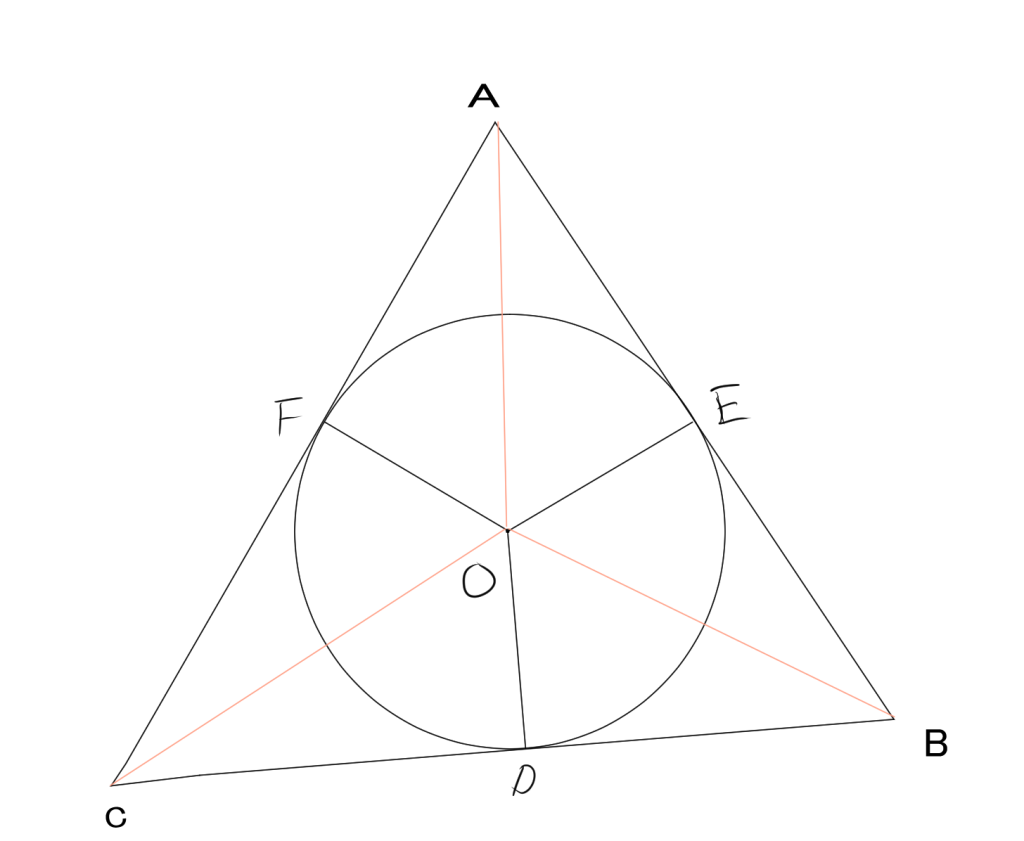
4. 内接円の半径を用いて三角形の面積を求める
内接円の半径を$r$、三角形の3辺の長さを$a、b、c$とします。このとき、三角形の面積を$S$とすると、
$$S=\dfrac{1}{2}(a+b+c)r$$
詳しくはこちらの記事で解説しています。
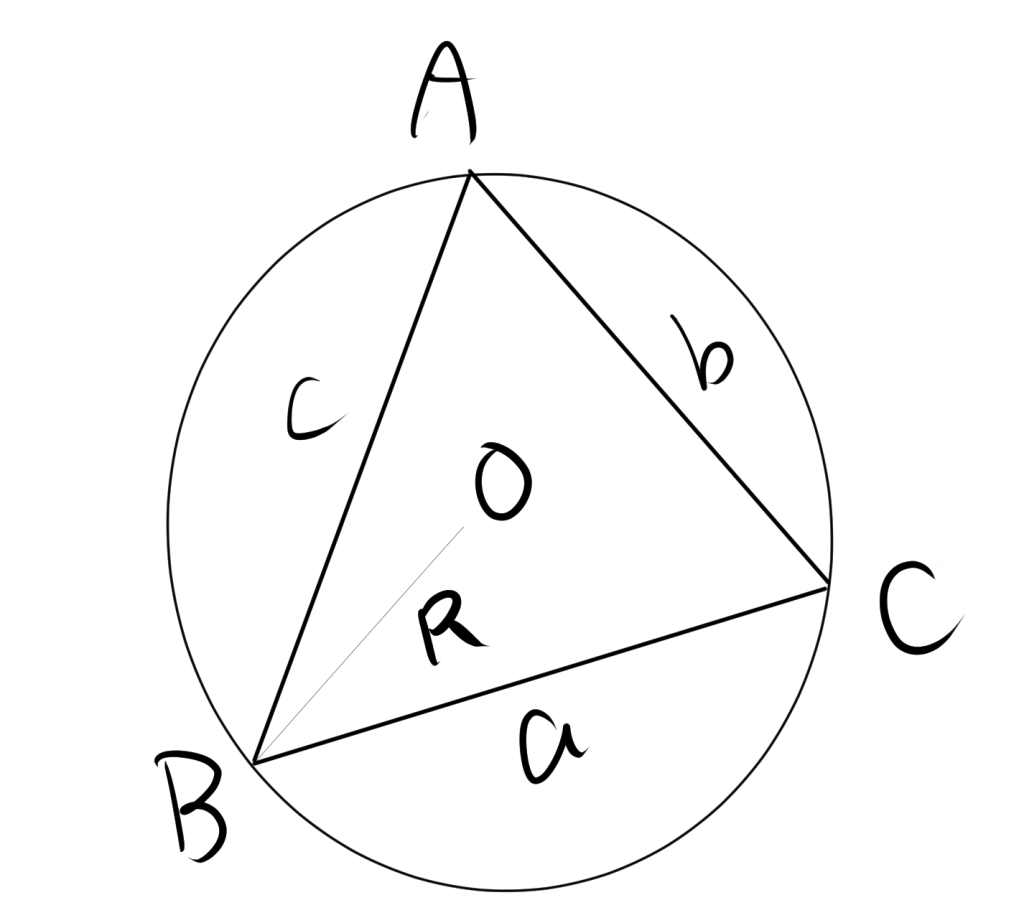
5. 外接円の半径を用いて三角形の面積を求める
$a$、$b$、$c$は三角形の辺の長さであり、$R$はその三角形を外接する円の半径、$S$を三角形の面積とすると、
$$S=\dfrac{abc}{4R}$$
詳しくはこちらの記事で解説しています。
6. 座標を用いて三角形の面積を求める
$A= (a_1,a_2),B = (b_1,b_2)$であるとき、三角形の面積Sは以下のようになる。
$$S=\dfrac{1}{2}|a_1b_2-a_2b_1|$$
詳しくはこちらの記事で解説しています。
7. ベクトルを用いて三角形の面積を求める
ベクトル$\overrightarrow a,\overrightarrow b$、三角形の面積をSとすると、三角形の面積は以下のようにあらわすことができます。
$$S=\dfrac{1}{2}\sqrt{|\overrightarrow a|^2|\overrightarrow b|^2-(\overrightarrow a \cdot \overrightarrow b)^2}$$
詳しくはこちらの記事で解説しています。
8. 外積を用いて三角形の面積を求める
外積の大きさは平行四辺形であり、$|\vec{a}\times\vec{b}|=|\overrightarrow a||\overrightarrow b|\sin\theta$とあらわされるから、三角形の面積はその半分である。したがって、
$$S=\dfrac{|\vec{a}\times\vec{b}|}{2}$$
詳しくはこちらの記事で解説しています。
PR
