【絶対値・複素数・ベクトル】三角不等式の証明と例題について

1. 三角不等式とは

三角不等式は、数学において絶対値、複素数、ベクトルの間で成り立つ不等式で、幾何的には三角形の辺の長さに関する性質を一般化したものです。それぞれのケースについて説明します。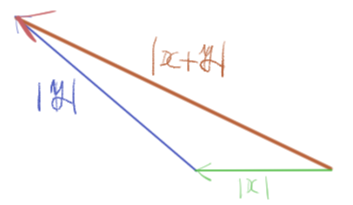

1.1. 絶対値における三角不等式

1.2. 複素数における三角不等式

1.3. ベクトルにおける三角不等式

2. 証明

2.1. 絶対値における三角不等式

$$|a + b|^2 -(|a| + |b|)^2$$

$$=a^2+2ab+b^2-(a^2+2|a||b|+b^2)$$

$$=2(ab-|ab|)$$

ここで、$|ab|\geq ab$より、$2(ab-|ab|)\leq 0$となるため、

$$|a + b|^2 -(|a| + |b|)^2 \leq 0$$

$$ \therefore |a + b| ^2\leq (|a| + |b|)^2$$

ここで、$|a + b|\geq 0, |a| + |b|\geq 0$より、不等式が得られます。

\[ |a + b| \leq  |a| + |b| \]

2.2. 複素数における三角不等式の証明

複素数 \(z = x + iy\) の絶対値は次のように定義されます。 \[ |z| = \sqrt{x^2 + y^2} \]

複素数 \(z_1\) と \(z_2\) をそれぞれ \(z_1 = x_1 + iy_1\) と \(z_2 = x_2 + iy_2\) とします。

左辺の複素数の和の絶対値の2乗を考えます。

\[ |z_1 + z_2|^2 = |(x_1 + x_2) + i(y_1 + y_2)|^2 \]

\[=(x_1 + x_2)^2 + (y_1 + y_2)^2 \]

右辺の$|z_1| + |z_2| $について考えると、

$$(|z_1| + |z_2|)^2=z_1^2+2|z_1||z_2|+z_2^2$$

$$=x_1^2 + x_2^2+y_1^2+y_2^2+2\sqrt{x_1^2 + x_2^2}\sqrt{y_1^2 +y_2^2}$$

$|z_1 + z_2|^2-(|z_1| + |z_2|)^2$を計算すると、

$$(|z_1| + |z_2|)^2-|z_1 + z_2|^2$$

$$=\sqrt{(x_1^2 + x_2^2)(y_1^2 +y_2^2)}-2x_1x_2-2y_1y_2$$

コーシー=シュワルツの不等式により、次の不等式が得られます。

\[ x_1x_2+y_1y_2 \leq \sqrt{(x_1^2 + x_2^2)(y_1^2 +y_2^2)}\]

$$\therefore \sqrt{(x_1^2 + x_2^2)(y_1^2 +y_2^2)}-2x_1x_2-2y_1y_2 \geq 0$$

したがって、 \[ |z_1 + z_2|^2 \leq (|z_1| + |z_2|)^2 \]

$|z_1 + z_2|\geq 0,|z_1| + |z_2|\geq 0$より、 \[ |z_1 + z_2| \leq |z_1| + |z_2| \]

2.3. ベクトルにおける三角不等式

\(\mathbf{a} = (a_1, a_2, \dots, a_n)\) 及び \(\mathbf{b} = (b_1, b_2, \dots, b_n)\) とします。

$(\|\mathbf{a}\| + \|\mathbf{b}\|)^2-\|\mathbf{a} + \mathbf{b}\| ^2$を計算します。

$$(\|\mathbf{a}\| + \|\mathbf{b}\|)^2-\|\mathbf{a} + \mathbf{b}\| ^2$$

$$=2(\|\mathbf{a}\|\|\mathbf{b}\|-\mathbf{a}\cdot\mathbf{b})$$

ここで、\(\mathbf{a}\) と \(\mathbf{b}\) の内積は以下のように表されます。
\[ \mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^n a_i b_i \]

次に、ベクトルのノルムは以下のように成分で表されます。

\[ \|\mathbf{a}\| = \sqrt{\sum_{i=1}^n a_i^2} \]

\[ \|\mathbf{b}\| = \sqrt{\sum_{i=1}^n b_i^2} \]

したがって、与えられた式は次のように表せます
\[ 2\left(\|\mathbf{a}\|\|\mathbf{b}\| – \mathbf{a}\cdot\mathbf{b}\right) = 2\left(\sqrt{\sum_{i=1}^n a_i^2} \cdot \sqrt{\sum_{i=1}^n b_i^2} – \sum_{i=1}^n a_i b_i \right) \]

コーシー=シュワルツの不等式により、次の関係が成り立ちます。

\[ \sqrt{\left( \sum_{i=1}^{n} a_i^2 \right) \left( \sum_{i=1}^{n} b_i^2 \right)} \geq  \sum_{i=1}^{n} a_i b_i \]

\[ \sqrt{\left( \sum_{i=1}^{n} a_i^2 \right) \left( \sum_{i=1}^{n} b_i^2 \right)} -\sum_{i=1}^{n} a_i b_i \geq  0 \]

したがって、

$$(\|\mathbf{a}\| + \|\mathbf{b}\|)^2-\|\mathbf{a} + \mathbf{b}\| ^2 \geq  0$$

$$\therefore (\|\mathbf{a}\| + \|\mathbf{b}\|)^2 \geq  \|\mathbf{a} + \mathbf{b}\| ^2$$

$\|\mathbf{a}\| + \|\mathbf{b}\|\geq 0 , \|\mathbf{a} + \mathbf{b}\|\geq 0$より、

\[ \|\mathbf{a} + \mathbf{b}\| \leq \|\mathbf{a}\| + \|\mathbf{b}\| \]

3. 三角不等式の例題

3.1. 例題1（実数における三角不等式）

 

1.三角不等式$ |x + y| \leq |x| + |y|$より $x$を$x+y$、$y$を$-yに置き替えると

\[ |x + y -y| \leq |x+y| + |-y| \]

\[ |x| \leq |x+y| + |y| \]

\[\therefore |x + y| \geq |x| – |y| \]

2.まず、\(x + y\)に対して三角不等式 \( |x + y| \leq |x| + |y| \)が成り立つ。

$x$を$x+y$、$y$を$z$に置き換えると、\[ |(x + y) + z| \leq |x + y| + |z| \]

$|x + y| + |z|$に着目すると、\( |x + y| \leq |x| + |y| \)が成り立つので、 \[|x + y| + |z|\leq |x| + |y| + |z| \]

したがって、次が成り立ちます。 \[ |x| + |y| + |z| \geq |x + y + z| \]

3.2. 例題2（n個の三角不等式）

$f_n= |a_1| + |a_2| + \cdots + |a_n|- |a_1 + a_2 + \cdots + a_n|$と置く。

\(n = 1\) の場合、

$$f_1=|a_1| -|a_1| =0\geq 0$$

となる。

\(n=k\) に対して、

$$f_k\geq0$$

$$ |a_1| + |a_2| + \cdots + |a_k|- |a_1 + a_2 + \cdots + a_k|\geq 0$$

が成り立つと仮定する。

\(n = k+1\) の場合を考えます。

$$f_{k+1}=|a_1| + |a_2| + \cdots + |a_k|+|a_{k+1}|- |a_1 + a_2 + \cdots +a_k+ a_{k+1}|$$

$$=|a_1| + |a_2| + \cdots + |a_k|+|a_{k+1}|-|(a_1 + a_2 + \cdots + a_k) + a_{k+1}|$$

$$\geq |a_1| + |a_2| + \cdots + |a_k|+|a_{k+1}| – (|a_1 + a_2 + \cdots + a_k| + |a_{k+1}|) $$

$$= |a_1| + |a_2| + \cdots + |a_k| -|a_1 + a_2 + \cdots + a_k|$$

$$=f_k\geq 0$$

$n=k+1$のときも、$f_{k+1}\geq0$が成り立つ。

したがって、数学的帰納法により、任意の自然数 \(n\) に対して$f_n\geq 0$が成り立つことが示されました。

$f_n\geq 0$より、

$$|a_1| + |a_2| + \cdots + |a_n|- |a_1 + a_2 + \cdots + a_n| \geq 0$$

$$ |a_1 + a_2 + \cdots + a_n| \leq |a_1| + |a_2| + \cdots + |a_n|$$