三角数の定義・三角数の定理・具体例・漸化式について

1. 三角数とは
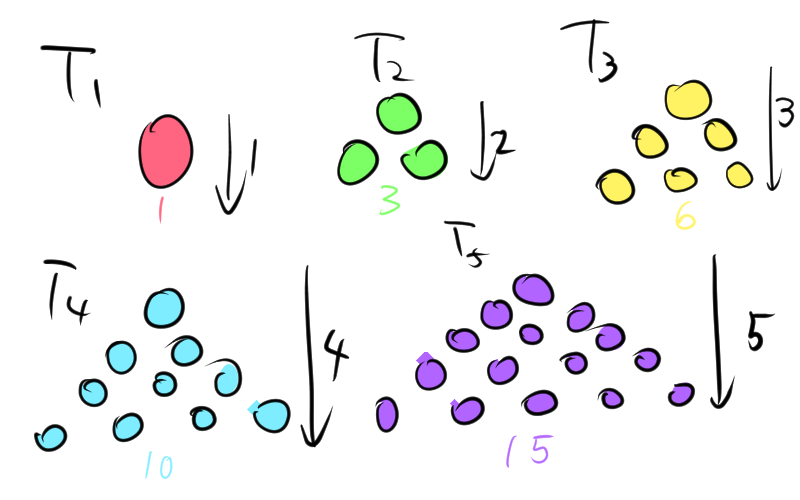
三角数は、図形数の一種で、点を使って正三角形の形に並べることができる自然数のことを指します。三角数は、1個の点から始まり、その次は2個の点、その次は3個の点、というように、各段に点を1つずつ増やして正三角形を形成します。
\[ T_n = \frac{n(n + 1)}{2} \]
例えば、最初のいくつかの三角数は次のようになります。
- \( T_1 = \frac{1(1 + 1)}{2} = 1 \)
- \( T_2 = \frac{2(2 + 1)}{2} = 3 \)
- \( T_3 = \frac{3(3 + 1)}{2} = 6 \)
- \( T_4 = \frac{4(4 + 1)}{2} = 10 \)
- \( T_5= \frac{5(5 + 1)}{2} = 15\)
これらの数は、点を正三角形に配置すると、次のような三角形の形に並べられます。
2. 三角数の性質
2.1. 三角数と二項係数
$_{n+1}\mathrm{C}_2=\dfrac{1}{2}n(n+1)$より、
$$T_n=\dfrac{1}{2}n(n+1)=_{n+1}\mathrm{C}_2$$
2.2. 隣接する三角数の和
$ T_n + T_{n-1} $を計算すると、
\[ T_n + T_{n-1} = \frac{n(n+1)}{2} + \frac{(n-1)n}{2} = n^2 \]
つまり、隣接する三角数 \( T_n \) と \( T_{n-1} \) の和は、\( n \) の2乗になります。
2.2.1. 具体例
例:1番目と2番目の三角数
1番目の三角数は \[ T_1 = \frac{1(1 + 1)}{2} = 1 \] 2番目の三角数は \[ T_2 = \frac{2(2 + 1)}{2} = 3 \] これらの和を計算すると、 \[ T_1 + T_2 = 1 + 3 = 4 \] 4は平方数(\( 2^2 \))です。
例:2番目と3番目の三角数
2番目の三角数は \[ T_2 = 3 \] 3番目の三角数は \[ T_3 = \frac{3(3 + 1)}{2} = 6 \] これらの和を計算すると、 \[ T_2 + T_3 = 3 + 6 = 9 \] 9は平方数(\( 3^2 \))です。
例:3番目と4番目の三角数
3番目の三角数は \[ T_3 = 6 \] 4番目の三角数は \[ T_4 = \frac{4(4 + 1)}{2} = 10 \] これらの和を計算すると、 \[ T_3 + T_4 = 6 + 10 = 16 \] 16は平方数(\( 4^2 \))です。
2.3. 三角数の3つの和(三角数の定理)
2.3.1. 具体例
以下に、具体例を示します。
整数 \( n \) が 、3個以下の三角数で表すことができる例をいくつか示します。
例 1: \( n = 3 \)
ここでは、\( n = 3 \) は三角数 \( T_2 = \frac{2 \times (2+1)}{2} = 3 \) で表されます。
よって、1個の三角数で \( n = 3 \) を表すことができます。
例 2: \( n = 11 \)
\( 11 = 10 + 1 \) であり、これは次のように三角数で表されます。
\( T_4 = \frac{4 \times (4+1)}{2} = 10 \)
\( T_1 = \frac{1 \times (1+1)}{2} = 1 \)
よって、2個の三角数 \( T_4 \) と \( T_1 \) で \( n = 11 \) を表すことができます。
例 3: \( n = 19 \)
\( 19 = 15 + 3 + 1 \) であり、これは次のように三角数で表されます。
\( T_5 = \frac{5 \times (5+1)}{2} = 15 \)
\( T_2 = \frac{2 \times (2+1)}{2} = 3 \)
\( T_1 = \frac{1 \times (1+1)}{2} = 1 \)
よって、3個の三角数 \( T_5 \), \( T_2 \), \( T_1 \) で \( n = 19 \) を表すことができます。
2.3.2. 証明
この性質を証明するために次の定理を利用します。
自然数は3つ以下の平方数の和で表すことができるという結果より、奇数の平方数を考えると次のようになる。
\[ 8N + 3 = (2x + 1)^2 + (2y + 1)^2 + (2z + 1)^2 \]
\[ 8N + 3 = (2x + 1)^2 + (2y + 1)^2 + (2z + 1)^2 \]
\[ 8N + 3 = 4(x^2 + y^2 + z^2) + 4(x + y + z) + 3 \]
\[ 8N = 4(x^2 + y^2 + z^2) + 4(x + y + z) \]
両辺を4で割ると、
\[ 2N = (x^2 + y^2 + z^2) + (x + y + z) \]
さらに、これを次のように整理します、
\[ N = \frac{x(x + 1)}{2} + \frac{y(y + 1)}{2} + \frac{z(z + 1)}{2} \]
$$\therefore N=T_x+T_y+T_z$$
このように、自然数 \( N \) は3つの整数 \( x, y, z \) の組み合わせで表されることが確認できます。
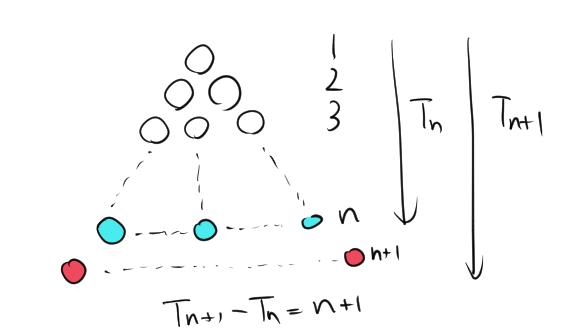
2.4. 三角数の漸化式1
$$T_{n+1}=T_n+n+1$$
三角形に〇を並べていくと$T_{n}$と$T_{n+1}$の差は$n+1$になるため、$T_{n+1}=T_n+n+1$は成り立つ。
$T_{n+1} $と \( T_n \) の差を求めます。
\[
T_{n+1} – T_n = \frac{(n+1)(n+2)}{2} – \frac{n(n+1)}{2}
\]
\[
= \frac{(n+1)[(n+2) – n]}{2}
\]
\[
= \frac{(n+1) \times 2}{2} = n+1
\]
これにより、次の漸化式が得られます。
\[ T_{n+1} = T_n + (n+1) \]
2.5. 三角数と漸化式2
三角数の定義に基づいて、\( T_{x+y} \) を計算します。
\[ T_{x+y} = \frac{(x+y)(x+y+1)}{2} \]
\[ T_{x+y} = \frac{x(x+1)}{2}+\frac{xy+y(x+1)+y^2}{2} \]
\[ T_{x+y} = T_x+\frac{2xy+y+y^2}{2} \]
\[ \therefore T_{x+y} = T_x+T_y+xy \]
2.6. 三角数と漸化式3
まず、左辺 \( T_{xy} \) を計算します。
\[ T_{xy} = \frac{xy(xy+1)}{2} \]
次に、右辺を計算します。
まず、 \( T_x T_y \) を計算します。
\[ T_x T_y = \frac{x(x+1)}{2} \times \frac{y(y+1)}{2} = \frac{x(x+1)y(y+1)}{4} \]
次に、\( T_{x-1} T_{y-1} \) を計算します。
\[ T_{x-1} T_{y-1} = \frac{(x-1)x}{2} \times \frac{(y-1)y}{2} = \frac{(x-1)xy(y-1)}{4} \]
右辺全体をまとめると、
\[ T_x T_y + T_{x-1} T_{y-1} = \frac{x(x+1)y(y+1) + (x-1)xy(y-1)}{4} \]
分子を展開して整理します。
\[ x y (xy + x + y + 1) + x y (xy – x – y + 1) = x y (2xy + 2) = 2xy(xy + 1) \]
したがって、右辺は次のようになります。
\[ T_x T_y + T_{x-1} T_{y-1} = \frac{2xy(xy+1)}{4} = \frac{xy(xy+1)}{2} \]
右辺 \( \frac{xy(xy+1)}{2} \) は、左辺 \( T_{xy} \) と一致するため、次の関係式が成り立つことが示されました。
\[ T_{xy} = T_x T_y + T_{x-1} T_{y-1} \]