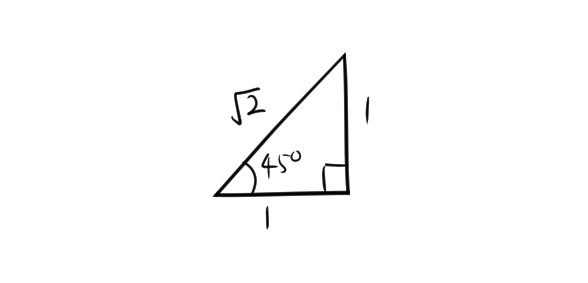三角比とは？正弦、余弦、正接と有名角について

はるか

三角比、まずは基本的な概念を押さえておくのが大事。

ふゅか

sin、cos、tanの3つだね！

1. 三角比（正弦、余弦、正接）

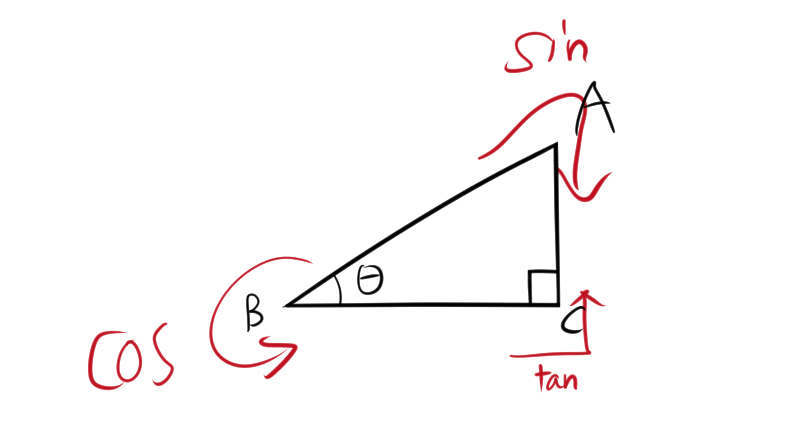
三角比とは、直角三角形の角度と辺の比の関係を表す数学の概念で、特に正弦（sin）、余弦（cos）、正接（tan）の3つがよく使われます。

2. 三角比の計算

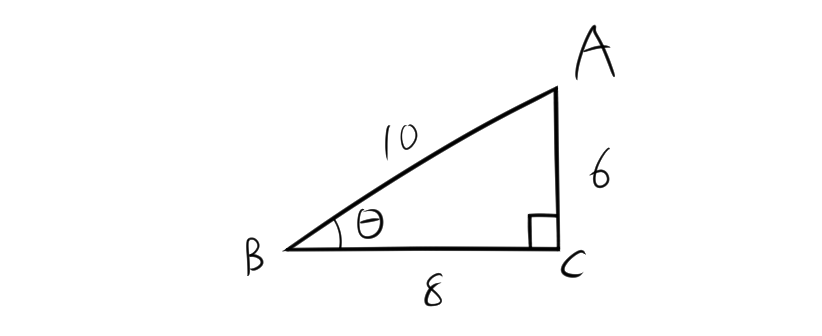
次のような三角形ABCを考えます。

2.1. 正弦（sin）

直角三角形の斜辺の長さが 10、角度 $θ$ に対するACの長さが 6 の場合、

$$\sin \theta = \frac{6}{10} = 0.6$$

2.2. 余弦（cos）

斜辺が 10 で、角度 $θ$ に対するBCの長さが 8 の場合、

$$\cos θ = \frac{8}{10} = 0.8$$

2.3. 正接（tan）

ACの長さが 6、BCの長さが 8 の場合、

$$\tan θ = \frac{6}{8} = 0.75$$

となります。

3. 有名角の三角比

ふゅか

それと、有名な角度の値も覚えておくと便利だよね。例えば、30°のsinは$\frac{1}{2}$になるよ。

はるか

うん、30°や45°、60°の値はよく使うから、すぐ出せるようにしておきたい。

三角比の計算では、30°、45°、60°といった有名な角度の値を覚えておくと非常に便利です。

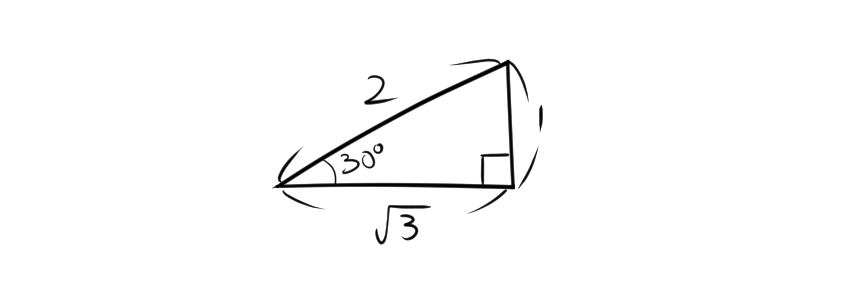
3.1. $30^\circ$ の三角比

• $\sin 30^\circ = \frac{1}{2}$
• $\cos 30^\circ = \frac{\sqrt{3}}{2}$
• $\tan 30^\circ = \frac{\sqrt{3}}{3}$

3.2. $45^\circ$ の三角比

• $\sin 45^\circ = \frac{\sqrt{2}}{2}$
• $\cos 45^\circ = \frac{\sqrt{2}}{2}$
• $\tan 45^\circ = 1$

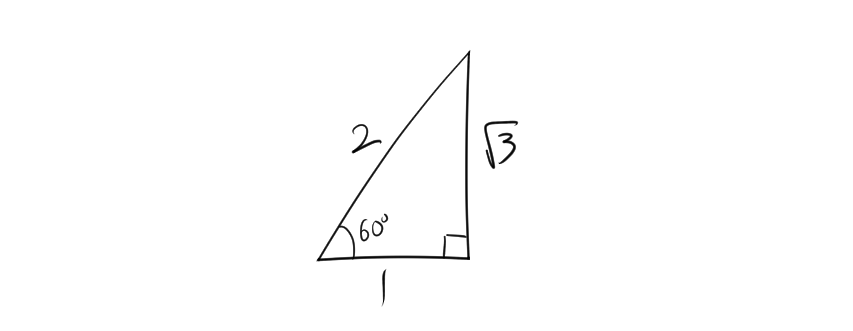
3.3. $60^\circ$ の三角比

• $\sin 60^\circ = \frac{\sqrt{3}}{2}$
• $\cos 60^\circ = \frac{1}{2}$
• $\tan 60^\circ = \sqrt{3}$

これらの有名角の三角比は、多くの数学の問題で頻繁に利用されます。